泸县九中高06级高考适应性考试
数 学(理科)2006.3、16
一、选择题
1、设集合E=![]() ,F=
,F=![]() ,则
,则![]() ( )
( )
A. 充分不必要条件 B必要不充分条件 C 充要条件 D不充分不必要条件
2、f(x)是定义在R上的奇函数,它的最小正周期是T,则![]() 的值是( )
的值是( )
A 0 B
![]() C
C ![]() D 无法确定
D 无法确定
3、设函数![]() ,则下列命题正确的是( )
,则下列命题正确的是( )
①图象上一定存在两点它们的连线平行于x轴。②图象上任意两点的连线都不平行于y轴。③图象关于直线y=x对称。④图象关于原点对称。
A ①③ B ②③ C ②④ D ③
4、曲线![]() 的一条切线平行于直线
的一条切线平行于直线![]() ,则切点p的坐标为( )
,则切点p的坐标为( )
(A)(0,-2)或(1,0) (B)(1,0)或(2,8)
(C)(-1,-4)或(0,-2) (D)(1,0)或(-1,-4)
5、如果消息A发生的概率为P(A),那么消息A所含的信息量为![]() 。若某人在一个有4排、8列的小型报告厅里听报告,则发布的以下4条消息中信息量最大的是( )
。若某人在一个有4排、8列的小型报告厅里听报告,则发布的以下4条消息中信息量最大的是( )
A 在某人在第4排 B 某人在第5列 C 某人在4排5列 D某人在任意一排
6、若函数f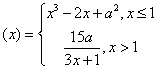 在点x=1处连续,则实数a等于( )
在点x=1处连续,则实数a等于( )
A 4 B ![]() C
C ![]() D
D ![]()
7、已知正四棱锥S-ABCD侧棱长为![]() ,底面边长为
,底面边长为![]() ,E是SA的中点,则异面直线BE与SC所成角的大小( )
,E是SA的中点,则异面直线BE与SC所成角的大小( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、若![]() ,(
,(![]() ),则
),则![]() 的取值范围是( )
的取值范围是( )
A ![]() B
B![]() C
C ![]() D
D ![]()
9、等差数列{an}中,a1 > 0,S3 = S11,则Sn中的最大值为( )
A S7 B S11 C S7和S8 D 无最大值
10、关于函数f(x)=lg![]() ,有下列命题:①函数y=f(x)的图象关于y轴对称。②当x>0时f(x)是增函数,当x<0时f(x)是减函数;③函数f(x)的最小值是lg2;④当
,有下列命题:①函数y=f(x)的图象关于y轴对称。②当x>0时f(x)是增函数,当x<0时f(x)是减函数;③函数f(x)的最小值是lg2;④当![]() 或x>1时,
f(x)是增函数.⑤f(x)无最大值,也无最小值。其中正确命题的序号是( )
或x>1时,
f(x)是增函数.⑤f(x)无最大值,也无最小值。其中正确命题的序号是( )
A① ③ B ②⑤ C ①③⑤ D ①③④
11、方程f(x)=x 的实根x0叫做函数f(x)的不动点,若函数f(x)=![]() 有唯一不动点,数列{an}满足a1=1000,
有唯一不动点,数列{an}满足a1=1000,
![]() 。则a2006=( )
。则a2006=( )
A 2002.5 B 2004.5 C 2006 D 2008
12、设![]() 的展开式按a 的降幂排列后第二项不大于第三项,则a 的取值范围是( )
的展开式按a 的降幂排列后第二项不大于第三项,则a 的取值范围是( )
A ![]() B
B ![]() C a ≤1 D a<1
C a ≤1 D a<1
13、复数z满足![]() ,那么z=
.
,那么z=
.
14、某市乘公车从A站到B站所需时间(单位:分)服从正态分布N(20,202),甲上午8:00从A站出发赶往B站见一位朋友乙,若甲只能在B站上午9:00前见到乙,则甲见不到乙的概率等于
。(参考数据:![]() ,
,![]() ,
,![]() )
)
| ○○○○○○○ |
15、霓虹灯的一个部位由七个小灯泡组成(如右图),
每个灯泡均可亮出红色或黄色.现设计每次变换只闪亮其中三个灯泡,且相邻两个不同时亮,则一共可呈现 种不同的变换形式(用数字作答).
16、已知A、B、C是半径为1的球面上的三点,A、B两点和A、C两点的球面距离都是![]() ,B、C两点的球面距离为
,B、C两点的球面距离为![]() ,则球心到平面ABC的距离为___________。
,则球心到平面ABC的距离为___________。
 泸县九中高06级高考适应性考试
泸县九中高06级高考适应性考试
数 学(理科)2006.3、18
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:
13、 . 14、
15、 16、___________。
17、(本小题12分)在![]() ,且
,且![]() .
.
(1) 求![]() 的值;
的值;
(2) 若b=2, ![]() 的面积S=3,求 a的值。
的面积S=3,求 a的值。
18、(本小题12分)一名学生在军训中练习射击项目,他命中目标的概率是![]() ,共射击6次.
,共射击6次.
(1) 求这名学生在第3次射击时,首次命中目标的概率;
(1) 求这名学生在射击过程中,命中目标![]() 的期望.
的期望.
19(12分)已知函数f(x)=a+bsinx+ccosx的图象经过点A(0,1)B(![]() ,1),当x
,1),当x![]() 时,f(x)的最大值为
时,f(x)的最大值为![]() 。
。
(1) 求f(x)的解析式;
(2) 由f(x)的图象按向量![]() 平移得到一个奇函数
平移得到一个奇函数![]() 的图象,求出一个符合条件的向量
的图象,求出一个符合条件的向量![]() 。
。
20、(12分)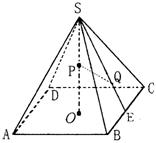 如图,已知正四棱锥S—ABCD的底面边长为4,高为6,点P是高的中点,点Q是侧面SBC的重心,求:
如图,已知正四棱锥S—ABCD的底面边长为4,高为6,点P是高的中点,点Q是侧面SBC的重心,求:
(Ⅰ) P、Q两点间的距离;
(Ⅱ)异面直线PQ与BS所成角的余弦值;
(Ⅲ)直线PQ与底面ABCD所成的角
21(12分)设函数![]()
![]()
(1)导数![]() .并证明
.并证明![]() 有两个不同的极值点x1、x2;
有两个不同的极值点x1、x2;
(2)若对于(1)中的x1、x2不等式![]() 成立,求a的取值范围。
成立,求a的取值范围。
22 (14分)过椭圆![]() 的右焦点F作直线l交椭圆于M、N两点,设
的右焦点F作直线l交椭圆于M、N两点,设![]()
(Ⅰ)求直线l的斜率k;
(Ⅱ)设M、N在椭圆右准线上的射影分别为M1、N1,求![]() 的值.
的值.
泸县九中高06级高考适应性考试
数学(理科)参考答案
一、选择题(每小题5分,共60分)BABDC,DBBAD,AD
二、填空题(每小题4分,共16分)13. ![]() , 14. 0.0228;
, 14. 0.0228;
15.
80; 16. ![]()
三、解答题(共76分)
17.解:(1)![]()
=![]()
=![]()
⑵![]()
![]() ,得
,得![]() 由余弦定理
由余弦定理
![]() =13
=13 ![]()
18(1)解:这名学生在各次射击中,击中目标与否相互独立
这名学生在第一、二次射击未击中目标,第三次击中目标,
![]()
(2)![]()
答:第3次射击时,首次击中目标的概率为![]() ,在射击过程中,命中目标数
,在射击过程中,命中目标数![]() 的期望是2。
的期望是2。
19.(1)由题意得![]() ,
,
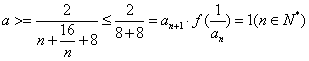 ,
,
又![]()
当![]()
当![]()
当![]()
![]()
![]()
(2)由(1)得![]()
![]() 按向量
按向量![]() 平移可以得到函数
平移可以得到函数![]() 的图象,
的图象,
![]()
![]() 是符合条件的一个向量:
是符合条件的一个向量: 


21.解:(1)![]()
令![]() 得,
得,![]() =0
=0![]()
![]()
![]()
![]() 方程有两个不同的实根
方程有两个不同的实根![]() ,令
,令![]() ,由
,由![]() 可知:
可知:
当![]() 时,
时,![]() ;当
;当![]() ;当
;当![]() ;
;
![]()
![]() 是极大值点,
是极大值点,![]() 是极小值点。
是极小值点。
(2)![]()
所以得不等式![]()
即![]()
又由(1)知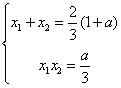 代入前面的不等式,两边除以(1+a),并
代入前面的不等式,两边除以(1+a),并
并化简得![]() ,解之:
,解之:![]() (舍去)
(舍去)
所以当![]() 时,不等式
时,不等式![]() 成立。
成立。
22. 解:(Ⅰ)F(![]() ) l:
) l:![]()
由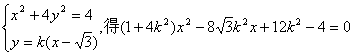
设M![]() ①
①
![]() ②
②
![]() ③
③
把①②代入③,并整理,得![]()
解得 ![]()
(Ⅱ)设![]() 的夹角为
的夹角为![]()
则由(Ⅰ)知![]() ∴
∴![]()
∴![]()