高考数学总复习第三讲:数形结合
一、专题概述 ---什么是数形结合的思想
数形结合的思想,就是把问题的数量关系和空间形式结合起来加以考察的思想.
恩格斯说:“纯数学的对象是现实世界的空间形式和数量关系.”“数”和“形”是数学中两个最基本的概念,它们既是对立的,又是统一的,每一个几何图形中都蕴含着与它们的形状、大小、位置密切相关的数量关系;反之,数量关系又常常可以通过几何图形做出直观地反映和描述,数形结合的实质就是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合起来,在解决代数问题时,想到它的图形,从而启发思维,找到解题之路;或者在研究图形时,利用代数的性质,解决几何的问题.实现抽象概念与具体形象的联系和转化,化难为易,化抽象为直观.
数形结合包括:函数与图象、方程与曲线、复数与几何的结合;几何语言叙述与几何图形的结合等.
二、例题分析
1.善于观察图形,以揭示图形中蕴含的数量关系.
观察是人们认识客观事物的开始,直观是图形的基本特征,观察图形的形状、大小和相互位置关系,并在此基础上揭示图形中蕴含的数量关系,是认识、掌握数形结合的重要进程.
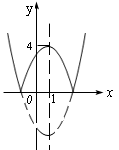
例1.函数![]() 的图象的一条对称轴方程是:
的图象的一条对称轴方程是:
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
分析:通过画出函数的图象,然后分别画出上述四条直线,逐一观察,可以找出正确的答案,如果对函数![]() 的图象做深入的观察,就可知,凡直线x=a通过这一曲线的一个最高点或一个最低点,必为曲线的一条对称轴,因此,解这个问题可以分别将
的图象做深入的观察,就可知,凡直线x=a通过这一曲线的一个最高点或一个最低点,必为曲线的一条对称轴,因此,解这个问题可以分别将![]() 代入函数的解析式,算得对应的函数值分别是:
代入函数的解析式,算得对应的函数值分别是:![]() ,其中只有–1是这一函数的最小值,由此可知,应选(A)
,其中只有–1是这一函数的最小值,由此可知,应选(A)
2.正确绘制图形,以反映图形中相应的数量关系.
观察图形,既要定性也要定量,借助图形来完成某些题时,仅画图示“意”是不够的,还必须反映出图形中的数量关系.
例2.问:圆![]() 上到直线
上到直线![]() 的距离为
的距离为![]() 的点共有几个?
的点共有几个?
分析 由平面几何知:到定直线L:![]() 的距离为
的距离为![]() 的点的轨迹是平行L的两条直线.因此问题就转化为判定这两条直线与已知圆的交点个数.
的点的轨迹是平行L的两条直线.因此问题就转化为判定这两条直线与已知圆的交点个数.
将圆方程变形为:![]() ,知其圆心是C(-1,-2),半径
,知其圆心是C(-1,-2),半径![]() ,而圆心到定直线L的距离为
,而圆心到定直线L的距离为![]() ,由此判定平行于直线L且距离为
,由此判定平行于直线L且距离为![]() 的两条直线中,一条通过圆心C,另一条与圆C相切,所以这两条直线与圆C共有3个公共点 (如图1)
的两条直线中,一条通过圆心C,另一条与圆C相切,所以这两条直线与圆C共有3个公共点 (如图1)
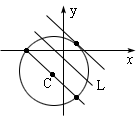 启示:正确绘制图形,一定要注意把图形与计算结合起来,以求既定性,又定量,才能充分发挥图形的判定作用.
启示:正确绘制图形,一定要注意把图形与计算结合起来,以求既定性,又定量,才能充分发挥图形的判定作用.
3.切实把握“数”与“形”的对应关系,以图识性以性识图.
数形结合的核心是“数”与“形”的对应关系,熟知这些对应关系,沟通两者的联系,才能把握住每一个研究对象在数量关系上的性质与相应的图形的特征之间的关联,以求相辅相成,相互转化.
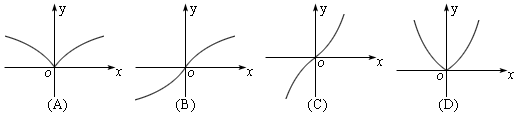
例3.判定下列图中,哪个是表示函数![]() 图象.
图象.
 分析 由
分析 由![]() =
=![]() ,可知函数
,可知函数![]() 是偶函数,其图象应关于y轴对称,因而否定(B)、(C),又
是偶函数,其图象应关于y轴对称,因而否定(B)、(C),又![]() ,
,![]() 的图象应当是上凸的,(在第Ⅰ象限,函数y单调增,但变化趋势比较平缓),因而(A)应是函数
的图象应当是上凸的,(在第Ⅰ象限,函数y单调增,但变化趋势比较平缓),因而(A)应是函数![]() 图象.
图象.
例4.如图,液体从一圆锥形漏斗注入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟注完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间t(分)的函数关系用图象表示只可能是().
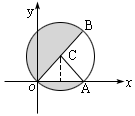
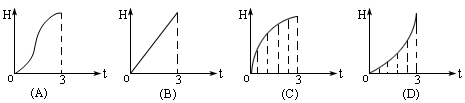
分析 由于圆柱中液面上升的速度是一个常量,所以H与t的关系不是(B),下落时间t越大,液面下落的距离H应越大,这种变化趋势应是越来越快,图象应当是下凸的,所以只可能是(D).
例5.若复数z满足![]() ,且
,且![]() ,则在复平面上对应点的图形面积是多少?
,则在复平面上对应点的图形面积是多少?
分析 满足![]() 的复数z对应点的图形是:以C(1,1)为圆心,
的复数z对应点的图形是:以C(1,1)为圆心,![]() 为半径的圆面,该圆面与
为半径的圆面,该圆面与![]() 图形的公共部分为图中所示阴影部分(要注意到∠AOC=45°)
图形的公共部分为图中所示阴影部分(要注意到∠AOC=45°)
因此所求图形的面积为:![]()
4.灵活应用“数”与“形”的转化,提高思维的灵活性和创造性.
在中学数学中,数形结合的思想和方法体现最充分的是解析几何,此外,函数与图象之间,复数与几何之间的相互转化也充分体现了数形结合的思想和方法.通过联想找到数与形之间的对应关系是实现转化的先决条件,而强化这种转化的训练则是提高思维的灵活性和创造性的重要手段.
例6.已知C<0,试比较![]() 的大小.
的大小. 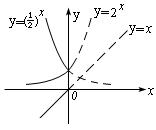
分析 这是比较数值大小问题,用比较法会在计算中遇到一定困难,在同一坐标系中,画出三个函数:![]() 的图象位于y轴左侧的部分,(如图)很快就可以从三个图象的上、下位置关系得出正确的结论:
的图象位于y轴左侧的部分,(如图)很快就可以从三个图象的上、下位置关系得出正确的结论:![]()
例7 解不等式![]()
解法一 (用代数方法求解),此不等式等价于:
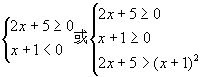 解得
解得![]()
故原不等式的解集是![]()
解法二 (采用图象法) 设![]() 即
即![]()
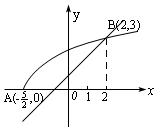
对应的曲线是以![]() 为顶点,开口向右的抛物线的上半支.而函数y=x+1的图象是一直线.(如图)
为顶点,开口向右的抛物线的上半支.而函数y=x+1的图象是一直线.(如图)
 解方程
解方程![]() 可求出抛物线上半支与直线交点的横坐标为2,取抛物线位于直线上方的部分,故得原不等式的解集是
可求出抛物线上半支与直线交点的横坐标为2,取抛物线位于直线上方的部分,故得原不等式的解集是![]() .
.
借助于函数的图象或方程的曲线,引入解不等式(或方程)的图象法,可以有效地审清题意,简化求解过程,并检验所得的结果.
| 例8 讨论方程 |
|
 9.已知直线
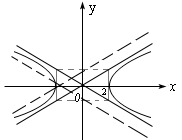
9.已知直线![]() 和双曲线
和双曲线![]() 有且仅有一个公共点,则k的不同取值有()
有且仅有一个公共点,则k的不同取值有()
(A)1个(B)2个(C)3个 (D)4个
分析:作出双曲线的图象,并注意到直线是过定点(![]() )的直线系,双曲线的渐近线方程为
)的直线系,双曲线的渐近线方程为![]()
∴过(![]() )点且和渐近线平行的直线与双曲线有且仅有一个公共点,此时k取两个不同值,此外,过(
)点且和渐近线平行的直线与双曲线有且仅有一个公共点,此时k取两个不同值,此外,过(![]() )点且和双曲线相切的直线与双曲线有且仅有一个公共点,此时k取两个不同的值,故正确答案为(D)
)点且和双曲线相切的直线与双曲线有且仅有一个公共点,此时k取两个不同的值,故正确答案为(D)
例9.已知直线![]() 和双曲线
和双曲线![]() 有且仅有一个公共点,则k的不同取值有()
有且仅有一个公共点,则k的不同取值有()
(A)1个(B)2个(C)3个 (D)4个
分析:作出双曲线的图象,并注意到直线是过定点(![]() )的直线系,双曲线的渐近线方程为
)的直线系,双曲线的渐近线方程为![]()
∴过(![]() )点且和渐近线平行的直线与双曲线有且仅有一个公共点,此时k取两个不同值,此外,过(
)点且和渐近线平行的直线与双曲线有且仅有一个公共点,此时k取两个不同值,此外,过(![]() )点且和双曲线相切的直线与双曲线有且仅有一个公共点,此时k取两个不同的值,故正确答案为(D)
)点且和双曲线相切的直线与双曲线有且仅有一个公共点,此时k取两个不同的值,故正确答案为(D)
例10.设点P(x,y)在曲线![]() 上移动,求
上移动,求![]() 的最大值和最小值.
的最大值和最小值.
解 曲线![]() 是中心在(3,3),长轴为
是中心在(3,3),长轴为![]() ,短轴为
,短轴为![]() 的椭圆.设
的椭圆.设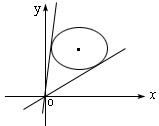
![]() ,即y=kx为过原点的直线系,问题转化为:求过原点的直线与椭圆相切时的斜率.(如图所示)
,即y=kx为过原点的直线系,问题转化为:求过原点的直线与椭圆相切时的斜率.(如图所示)
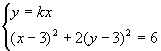 消去y得
消去y得![]()
![]()
解得:![]()
故![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]()
例11.求函数![]() (其中a,b,c是正常数)的最小值.
(其中a,b,c是正常数)的最小值.
分析 采用代数方法求解是十分困难的,剖析函数解析式的特征,两个根式均可视为平面上两点间的距离,故设法借助于几何图形求解.如图
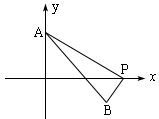 设A(0,a),B(b,-c)为两定点,P(x,0)为x轴上一动点,
设A(0,a),B(b,-c)为两定点,P(x,0)为x轴上一动点,
则![]()
![]() 其中的等号在P为线段AB与x轴的
其中的等号在P为线段AB与x轴的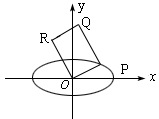 交点外,即
交点外,即![]() 时成立.
时成立.
故y的最小值为![]()
例12.P是椭圆![]() 上任意一点,以OP为一边作矩形O P Q R(O,P,Q,R依逆时针方向排列)使OR=2OP,求动点R的轨迹的普通方程.
上任意一点,以OP为一边作矩形O P Q R(O,P,Q,R依逆时针方向排列)使OR=2OP,求动点R的轨迹的普通方程.
分析 在矩形O P Q R中(如图),由∠POR=90°,OR=2OP可知,OR是OP逆时针旋转90°,并将长度扩大为原来的2倍得到的.这一图形变换恰是复数乘法的几何意义,因此,可转化为复数的运算,找到R和P的两点坐标之间的关系,以求得问题的解决.
解,设R点对应的复数为:![]() ,P点对应的复数为
,P点对应的复数为![]()
则![]()
故![]() 即
即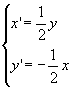 由点
由点![]() 在椭圆上可知有:
在椭圆上可知有: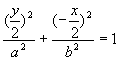
整理得:![]() 就是R点的轨迹方程,表示半长轴为2a,半短轴为2b,中心在
就是R点的轨迹方程,表示半长轴为2a,半短轴为2b,中心在 原点,焦点在y轴上的椭圆.
原点,焦点在y轴上的椭圆.
三解题训练
1.求下列方程实根的个数:
(1)![]()
(2)![]()
(3)![]()
2.无论m取任何实数值,方程![]() 的实根个数都是()
的实根个数都是()
(A)1个(B)2个(C)3个(D)不确定
3.已知函数![]() 的图象如右图则()
的图象如右图则()
(A)b∈(-∞,0)(B)b∈(0,1)
(C)b∈(1,2) (D)b∈(2,+ ∞)
4.不等式![]() 的解集是()
的解集是()
(A)(0,+∞)(B)(0,1)(C)(1,+∞)(D)(–∞,0)
5.不等式![]() 一定有解,则a的取值范围是()
一定有解,则a的取值范围是()
(A)(1,+∞)(B)[1,+ ∞](C)(-∞,1)(D)(0,1]
6.解下列不等式:
(1)![]() (2)
(2)![]()
7.复平面内点A、B分别对应复数2,2+i,向量![]() 绕点A逆时针方向旋转
绕点A逆时针方向旋转![]() 至向量
至向量![]() ,则点C对应的复数是_______.
,则点C对应的复数是_______.
8.若复数z满足z<2,则arg(z-4)的最大值为___________
9.若复数z满足
10.函数![]() 的图象是平面上两定点距离之差的绝对值等于定长的点的轨迹,则这两定点的坐标是( )
的图象是平面上两定点距离之差的绝对值等于定长的点的轨迹,则这两定点的坐标是( )
(A)(–![]() ,–
,–![]() )(
)(![]() ,
,![]() )(B)(–
)(B)(–![]() ,
,![]() )(
)(![]() ,–
,–![]() )
)
(C)(–2![]() ,2
,2![]() )(2
)(2![]() ,2
,2![]() )(D)(2
)(D)(2![]() ,–2
,–2![]() )(–2
)(–2![]() ,2
,2![]() )
)
11.曲线![]() 与直线
与直线![]() 的交点个数是().
的交点个数是().
(A)0(B)1 (C)2(D)3
12.曲线![]() 与直线
与直线![]() 有两个交点,则实数k的取值是()
有两个交点,则实数k的取值是()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
13.已知集合![]() ,
,![]() 满足
满足![]() ,求实数b的取值范围.
,求实数b的取值范围.
14.函数![]() 的值域是()
的值域是()
(A)![]() (B)
(B)![]()
(C)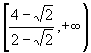 (D)
(D)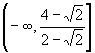
四、练习答案
1.(1)2个(2)63个(3)2个
提示:分别作出两个函数的图象,看交点的个数.
2.B、 提示:注意到方程右式,![]() 是过定点(
是过定点(![]() ,0)的直线系.
,0)的直线系.
3.A、 提示:由图象知f(x)=0的三个实根是0,1,2这样,函数解析式可变形f(x)=ax(x-1)(x-2),又从图象中可以看出当x∈(0,1)∪(2,+∞)时,f(x)>0.而当x>2时,x,(x-1),(x-2)均大于0,所以a>0,而![]() 可知b=-3a<0,故选(A)
可知b=-3a<0,故选(A)
4.A
5.A
6.(可以利用图象法求解)
(1)x≤-1或0<x≤3 (2)x≤-1
7.1
8.210°
9.
10.A
11.D 提示:在曲线方程中,分x≥0或x<0两种情形讨论,作出图形即可.
12.C
13.![]()
14.A 提示:f(x)可以视作:A(cosx,sinx),B(1,2),则f(x)=kAB,而A点为圆x2+y2=1上的动点