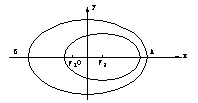高考数学总复习第五讲：应用问题

高考数学总复习第五讲：应用问题

一、专题简介

著名数学家华罗庚曾说过：宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学．可见数学在现实生活中的应用之广泛．
　　从93年开始，为考察考生的分析问题与决问题的能力，在高考数学试题中引入了一定数量的联系生产和生活实际以及相关学科的应用问题．
　　高考中的应用性问题是指具有实际背景或具有实际意义的数学问题，以考察学生的数学知识、方法与能力为主，着重考察学生应用数学的意识．
　　高考中出现的应用性问题，大体可分为三类：
　　第一类是教科书或其它书籍中已经出现过的，从实际生活中概括出来的应用性问题．
　　第二类是与横向学科，如化学、物理、生物等有联系的问题．
　　第三类是有实际生活背景，题意新颖的应用问题．
　　解数学应用问题从一般步骤是：
　　一要阅读理解，认真审题，分析题意，认清已知条件及要求的结论．
　　二要理清各种量（已知与已知、已知与未知）之间的关系，紧紧抓住各种变量之间的关系，分析各种制约条件，将实际问题转化为数学问题．
　　三构造模型、通过对各种关系的分析，形成数学框架，转化为函数、方程、不等式、数列等数学问题，再设法去解决．

二、例题分析

1.代数应用题
　　例1．在测量某物理量的过程中，因仪器和观测的误差，使得n次测量分别得到a₁,a₂,…a_n共n个数据，我们规定所测量的物理量的“最佳近似值”a是这样一个量：与其他近似值比较，a与各数据的差的平方和最小，依此规定，从a₁,a₂,…a_n推出的a=______________．
　　分析：本题是与其它学科相关的数学应用问题，要正确理解题意，并能把文字语言转化为符号语言．
　　解：依题意，本题即是求使 的最小值时，a的取值．
　　∵ ，
　　故当 时，f(a)最小．
　　例2.《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过800元的部分不必纳锐，超过500元的部分为全月应纳税所得额，此项税款按下表分段累进计算：

全月应纳税所得额	税率
不超过500元的部分	5%
超过500元至2000元的部分	10%
超过2000元至5000元的部分	15%

　　　 某人一月份应交纳此项税款26.78元，则他的当月工资、薪金所得介于
　　（A）800～900元 （B）900元～1200元 （C）1200～1500元 （D）1500～2000元
　　分析：注意分类讨论思想的应用．
 思路一：若收入1300元应纳税：500×5%=25元<26.78元
　　∴此人收入超过1300元，淘汰A、B．
　　若收入1500元应纳税：500×5%+200×10%=45元>26.78元
　　∴此人收入低于1500元，排除D，故选C．
　　思路2：设全月应纳税所得额为x元．
　　当x<500时，由题意知　x·5%=26.78
　　∴ 故与题意不符合．
　　当500<x<2000元时，则500×5%+(x–500) ×10%=26.78
　　∴x=517.8
　　∴当月工资、薪金所得额为800+517.8=1317.8元．
　　故选C．
　　例3．设计某高速公路时，要求最低车速50千米/小时，最小车距为l千米（l是定值），并且车速v与车距d之间必须满足关系 ,求：
　　（Ⅰ）常数k的值：
　　（Ⅱ）这条高速公路的一条车道上每小时的最高车流量．（单位时间车流量=车速/车距）
　　解：（Ⅰ）由题意，将v=50，d=l代入解析式中可求得
　　（Ⅱ） ．
　　设每小时车流量为Q，则
　　
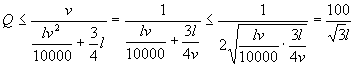
　　（由实际问题， 皆为正值）
　　当且仅当 ，即 时等号成立．
　　而 所以当车速为 千米/小时，此高速公路一条车道上每小时的最大车流量为 辆．
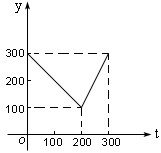
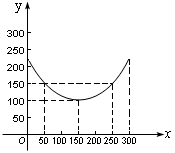
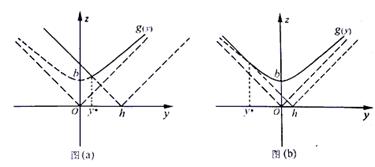
　　例4.某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场售价与上市时间的关系用图一的一条折线表示；西红柿的种植成本与上市时间的关系用图二的抛物线表示．

图一	图二

  　 （Ⅰ）写出图一表示的市场售价与时间的函数关系式P=f(x)；写出图二表示的种植成本与时间的函数关系式Q=g(t)
　　（Ⅱ）认定市场售价减去种植成本为纯收益，向何时上市的西红柿纯收益最大？
　　（注：市场售价和种植成本的单位：元/10²kg，时间单位：天）
　　分析：要根据函数图象正确建立函数关系式，然后求最值．
　　解：由图一可得市场售价与时间的函数关系为
　　
　　由图二可得种植成本与时间的函数关系为，
　　
Ⅱ）设t时刻的纯收益h(t),则由题意得．
　　
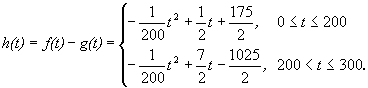
　　当0≤t≤200时，配方整理得
　　 ，
　　∴t=50时，h(t)取得区间[0，200]上的最大值100；
　　当 时，配方整理得，
　　
　　∴当t=300时，h(t)取得区间(200,300]上的最大值87.5
　　　 综上，由100>87.5可知，h(t)在区间[0，300]上可以取得最大值100，此时t=50，即从二月一日开始的第50天时，上市的西红柿纯收益最大．
　　例5某企业年初有资金1000万元，如果该企业经过生产经营每年资金增长率均为50%，但每年年底都要扣除消费基金x万元，余下资金投入再生产，为实现经过5年资金达到2000万元（扣除消费资金后），那么每年扣除消费基金x应是多少万元（精确到万元）？
　　解：依题意，第一年年底扣除消费资金后，投入再生产资金为1000+1000×50%–x=1000×
　　　 第二年投入再生产资金为
　　
　　 ……
　　   第五年投入再生产资金为
　　
　　化简得：
　　故x≈424（万元）
　　答：每年扣除消费资金为424元．
　　说明：本题关键是寻求每年投入再生产资金的规律，构造数列模型来解题．

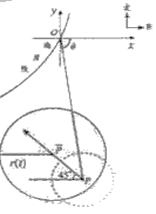
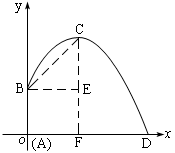
例６在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O（如图）的东偏南　　　　

方向300km的海面P处，并以20km/h的速度向西偏北45°方向移动，台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大问几小时后该城市开始受到台风的侵袭？

解：如图建立坐标系：以O为原点，正东方向为x轴正向.

　　　　在时刻：t（h）台风中心的坐标为

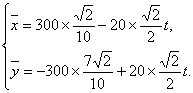
　　　　此时台风侵袭的区域是，

　　　　其中t+60，

　　　　若在t时，该城市O受到台风的侵袭，则有

即

即，　 解得.

答：12小时后该城市开始受到台风气侵袭

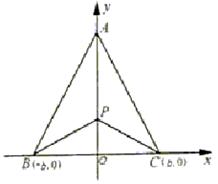
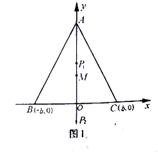
例７、有三个新兴城镇，分别位于A，B，C三点处，且AB=AC=a，BC=2b.今计划合建一个中心医院，为同时方便三镇，准备建在BC的垂直平分线上的P点处，（建立坐标系如图）

　 （Ⅰ）若希望点P到三镇距离的平方和为最小，

 点P应位于何处？

　 （Ⅱ）若希望点P到三镇的最远距离为最小，

　　　　 点P应位于何处？

本小题主要考查函数，不等式等基本知识，考查运用数学知识分析问题和解决问题的能力.　　（Ⅰ）解：由题设可知，记设P的坐标为（0，），则P至三镇距离的平方和为　所以，当时，函数取得最小值.　答:点P的坐标是

（Ⅱ）解法一：P至三镇的最远距离为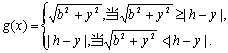

　　由解得记于是

　　　当即时，在[上是增函数，而上是减函数. 由此可知,当时,函数取得最小值. 当即时,函数在[上,当时,取得最小值,而上为减函数,且 可见, 当时, 函数取得最小值. 答当时,点P的坐标为当时,点P的坐标为(0,0),其中

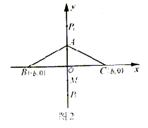
　解法二:P至三镇的最远距离为　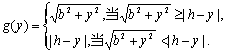由解得

　记于是

　　　

　当的图象如图，因此，当时，函数取得最小值.

　当即的图象如图，因此，当时，函数取得最小值.

答：当时，点P的坐标为当，点P的坐标为（0，0），其中

　　　 解法三：因为在△ABC中，AB=AC=所以△ABC的外心M在射线AO上，其坐标为，

　 且AM=BM=CM. 当P在射线MA上，记P为P1；当P在射线MA的反向延长线上，记P为P2，

若（如图1），则点M在线段AO上，

这时P到A、B、C三点的最远距离为

P1C和P2A，且P1C≥MC，P2A≥MA，所以点P与外心M

重合时，P到三镇的最远距离最小.

 若(如图2),则点M在线段AO外,这时

P到A、B、C三点的最远距离为P1C或P2A，

　且P1C≥OC，P2A≥OC，所以点P与BC边中点O重合时，

P到三镇的最远距离最小为.

答：当时，点P的位置在△ABC的外心

；当时，点P的位置在原点O.

例８、某城市2001年末汽车保有量为30万辆，预计此后每年报废上一年末汽车保有量的，并且每年新增汽车数量相同。为保护城市环境，要求该城市汽车保有量不超过万量，那么每年新增汽车数量不应超过多少辆？

解：设2002年末汽车保有量为万辆，以后各年末汽车保有量依次为万辆，万辆……，每年新增汽车万辆，则

，

对于，有

………………

∴

当，即时，

当，即时，并且数列逐项增加，可以任意靠近

因此，如果要求汽车保有量不超过60万辆，即

则，即（万辆）

综上，每年新增汽车不应超过万辆。

例９、　　某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元。该厂为鼓励销售商订购，决定当一次订购量超过100件时，每多订购一件，订购的全部服装的出厂单价就降低0.02元。根据市场调查，销售商一次订购量不会超过500件。

（I）设一次订购量为x件，服装的实际出厂单价为P元，写出函数的表达式；

（II）当销售商一次订购了450件服装时，该服装厂获得的利润是多少元？

（服装厂售出一件服装的利润＝实际出厂单价－成本）

本小题主要考查函数的基本知识，考查应用数学知识分析问题和解决问题的能力。

  解：（I）当时，

　　当时，

　　所以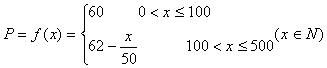

　　（II）设销售商的一次订购量为x件时，工厂获得的利润为L元，则

　　

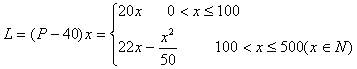
　　当时，

　　因此，当销售商一次订购了450件服装时，该厂获利的利润是5850元。

例１０、本题共有2个小题，第一小题满分6分，第2小题满分8分.

某市2003年共有1万辆燃油型公交车。有关部门计划于2004年投入128辆电力型公交车，

随后电力型公交车每年的投入比上一年增加50%，试问：

(1)　　该市在2010年应该投入多少辆电力型公交车？

(2)　　到哪一年底，电力型公交车的数量开始超过该市公交车总量的？

解.(1)该市逐年投入的电力型公交车的数量组成等比数列，其中

则在2010年应该投入的电力型公交车为（辆）。

(2)记，依据题意，得。于是（辆），即，

则有因此。所以，到2011年底，电力型公交车的数量开始超过该市公交车总量的。

　　2．几何应用题．
　　例１１．如右图，设田地喷灌水管AB高出地面1.5米，在B处有一个自动旋转的喷水头，一瞬间，喷出水流是抛物线状，喷头B与水流最高点C的连线与水平地面成45°角，若C比B高出2米，在所建的坐标系中，求水流的落地点D到点A的距离是多少米？
　　分析：本题要构造解析几何模型，其关键是确定抛物线的方程．
　　解. 依题可知.BE=CE=2（米），CF=CE+EF=3.5（米），点B的坐标为（0,1.5）
　　∴抛物线的方程为
　　由于它经过点B，故
　　 ∴4a=–2, ∴ .
　　　故抛物线的方程为
　　当y=0时，
　　∴
　　　 即水流落地点D和点A的距离为
　　例7.如右图是抛物线型拱桥，设水面宽AB=18米，拱项离水面的距离为8米，一货船在水面上的部分的横断面为一矩形CDEF．
　　（1）若矩形的长CD=9米，那么矩形的高DE不能超过多少米才能使船通过拱桥？
　　（2）求矩形面积S的“临界值”M：即当S≤M时，适当调整矩形的长和高，船能通过拱桥；而当S>M时，无论怎样调整矩形的长和高，船都不能通过拱桥．
　　分析：本题确切指明是抛物线型，因此关键是确定抛物线段的方程．
　　解：（1）如图，以O点为原点，过O平行AB的直线为x轴以线段AB的垂直平分线为y轴建立直角坐标系．则B（9，—8）

设抛物线方程为 (p>0) 　　　 ∵B点在抛物线上， 　　∴81=–2p（–8） ∴ 　　　　∴抛物线的方程为 　　当 时，y=–2，∴DE=6， 　　所以当矩形的高DE不超过6米时，才能使船通过拱桥．

　　（2）设
　　则CD=2x,
　　　 ∴
　　　
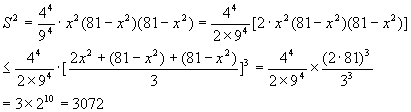
　　　 当且仅当 即 ,8取得最大值32 平方米，∴矩形面积S的临界值M为 。

例１２、如图，某隧道设计为双向四车道，车道总宽22米，要求通行车辆限高4.5米，隧道全长2.5千米，隧道的拱线近似地看成半个椭圆形状。

（1）若最大拱高h为6米，则隧道设计的拱宽l是多少？

（2）若最大拱高h不小于6米，则应如何设计拱高h和拱宽l，才能使半个椭圆形隧道的土方工程量最小？

（半个椭圆的面积公式为。柱体体积为：底面积乘以高。本题结果均精确到0.1米）

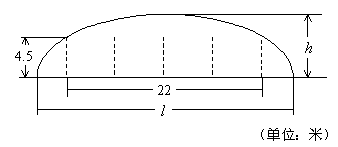
［解］（1）如图建立直角坐标系，则点P（11，4.5）

椭圆方程为

将与点P坐标代入椭圆方程，得，此时

因此隧道的拱宽约为33.3米。

（2）［解一］由椭圆方程

得

因为，即，且

所以

当S取最小值时，有，得

此时

故当拱高约为6.4米，拱宽约为31.1米时，土方工程量最小

［解二］由椭圆方程，得

于是

即，当S取最小值时，有

得，，以下同解一

例１３、　 2003年10月15日9时，“神舟”五号载人飞船发射升空，于9时9分50秒准确进入预定轨道，开始巡天飞行。该轨道是以地球的中心为一个焦点的椭圆。选取坐标系如图所示，椭圆中心在原点。近地点A距地面200km，远地点B距地面350km。已知地球半径R＝6371km。

（I）求飞船飞行的椭圆轨道的方程；　　

（II）飞船绕地球飞行了十四圈后，于16日5时59分返

回舱与推进舱分离，结束巡天飞行，飞船共巡天飞行了约

，问飞船巡天飞行的平均速度是多少km/s？

（结果精确到1km/s）（注：km/s即千米/秒）

本小题主要考查椭圆等基本知识，考查分析问题和解决问题的能力。满分14分

　　解：（I）设椭圆的方程为　　由题设条件得

　　

　　解得　　所以

　　

　　所以椭圆的方程为

　 （注：由得椭圆的方程为，也是正确的。）

（II）从15日9时到16日6时共21个小时，合21×3600秒

　　减去开始的9分50秒，即9×60＋50＝590（秒），再减去最后多计的1分钟，共减去590＋60＝650（秒）　　得飞船巡天飞行的时间是　　（秒）

　　平均速度是（千米/秒）　　所以飞船巡天飞行的平均速度是8km/s。

例１４、A、B两个代表队进行乒乓球对抗赛，每队三名队员，A队队员是A₁，A₂，A₃，B

队队员是B₁，B₂，B₃，按以往多次比赛的统计，对阵队员之间胜负概率如下：

对阵队员	A队队员胜的概率	A队队员负的概率
A1对B1
A2对B2
A3对B3

现按表中对阵方式出场，每场胜队得1分，负队得0分，设A队、B队最后所得总

分分别为ξ、η

　 （1）求ξ、η的概率分布；

　 （2）求Eξ，Eη.

本小题考查离散型随机变量分布列和数学期望等概念，考查运用概率知识解决实际问题的能力

解：（1）ξ、η的可能取值分别为3，2，1，0.

，

根据题意知ξ+η=3，所以　P(η=0)=P(ξ=3)=, P(η=1)=P(ξ=2)=

P(η=2)=P(ξ=1)= ,　P(η=3)=P(ξ=0)= .

　 （2）； 因为ξ+η=3，所以　

三、巩固练习

1.某种细菌在培养过程中，每20分钟分裂一次（一个分裂为两个），经过3小时，这种细菌由1个可以繁殖成（　　）
　　（A）511个　 （B）512个　　（C）1023个　 （D）1024个
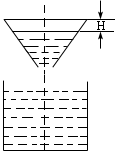
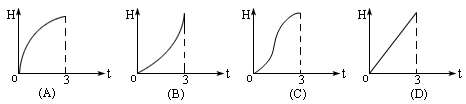
　　2. 如图所示，液体从一圆锥形漏斗注入一圆柱形桶中，开始时，漏斗盛满液体，经过3min漏完，已知圆柱中液面上升的速度是一个常量，设H是圆锥形漏斗中液面下落的距离，则H与下落时间t（min）的函数关系的图示只可能是（　　）

　　　 3.1992年底世界人口达到54.8亿，若人口的年平均增长率为x%,2000年度世界人口数为y（亿），那么y与x的函数关系式是____________．
　　4.某商店每月利润稳步增长，去年12月份的利润是当年1月份利润的k倍，则该商店去年每月利润的平均增长率为(　　 ).
　　（A） 　（B） 　 （C） 　　（D）
　　5.造纸厂用若干台效率相同的抽水机从河里往蓄水池灌水，若所有机械同时开动，则需24小时灌满水池，若一台接一台地开动，每相邻两台启动时间间隔都相同，那么灌满水池时，第一台的工作时间是最后一台的7倍，问第一台工作了多少时间？
　　6.某化工厂生产某种化工产品，根据市场调查，年产量需不小于150吨且不大于220吨．这时，其生产的总成本y（万元）与年产量x(吨)之间的函数可近似的表示为 ．
　　（Ⅰ）当年产量为多少吨时，每吨的平均成本最低，并求每吨最低平均成本．
　　（Ⅱ）若每吨平均出厂价为16万元，求年产量为多少吨时，可获得最大的年利润；并求出最大年利润．
　　7.某地区上年度电价为0.8元/kw·h，年用电量为akw·h，本年度计划将电价降到0.55元/kw·h到0.75元/kw·h之间，而用期望电价为0.4元/kw·h，经测算，下调电价后新增的用电量与实际电价和用户期望电价的差成反比（此例系数为k）
　　该地区电力的成本价为0.3元/kw·h．
　　（Ⅰ）写出本年度电价下调后，电力部分的收益y与实际电价x的函数关系式；
　　（Ⅱ）设k=0.2a,当电价最低定为多少时，可保证电力部分的收益比上年至少增长20%？
　　（注：收益=实际用电量×（实际电价–成本价）

四、练习解析

1.选（B）.提示：细菌繁殖的问题是一个等比数列问题，其首项为1，公比为2，经过3小时分裂9次，因此末项是a₁₀　∴
　　　2.选（B），提示：圆柱中液面上升速度为一个常量，即相同时间内漏入圆柱中的液体体积相同，则在圆锥漏斗中，相同时间内保持漏出液体体积相同，是H的增长越来越快．
　　3.
　　　 4.选（B）提示：设一月份为a，月平均增长率为m,则 　 ∴ ．
　　5.解：设有n台抽水机，每相邻两台启动时间间隔为d小时，最后一台工作时间为t小时，依题意，得.
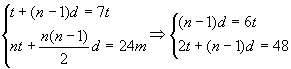　　　　  ∴t=6
　　　答：第一台工作时间为42小时．

 6．解：（Ⅰ）每吨平均成本为 （万元）．
　　则
　　当且仅当 即x=200时取等号．
　　又150≤200≤220，∴年产量为200吨时，每吨平均成本最低为10万元．
　　（Ⅱ）设年获得总利润为Q万元，则
　　
　　∵ 而Q在 时是增函数，
　　∴x=220时，
　　∴年产量为220吨时，可获得最大利润1280万元．
　　7.解：(Ⅰ)设下调后的电价为x元/kw·h，依题意知：用电量增至 电力部门的收益为
　　(Ⅱ)依题意，有
　　
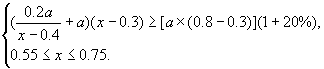
　　整理得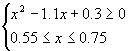
　　解此不等式组得0.60≤x≤0.75
　　　 答：当电价最低定为0.60元/kw·h仍可保证电力部门的收益比上年至少增长20%