高考数学总复习第一讲:函数与方程
函数描述了自然界中量的依存关系,反映了一个事物随着另一个事物变化而变化的关系和规律.函数思想的实质是剔除问题的非数学特征,用联系和变化的观点提出数学对象,抽象其数学特征,建立函数关系.
在解决某些数字问题时,先设定一些未知数,然后把它们当作已知数,根据题设本身各量间的制约,列出等式,所设未知数沟通了变量之间的关系,这就是方程的思想.
函数与方程是两个不同的概念,但它们之间有着密切的联系,一个函数若有解析表达式,那么这个表达式就可看成是一个方程.一个二元方程,两个变量存在着对应关系,如果这个对应关系是函数,那么这个方程可以看成是一个函数,一个一元方程,它的两端可以分别看成函数,方程的解即为两个函数图象交点的横坐标,因此,许多有关方程的问题可以用函数的方法解决;反之,许多有关函数的问题则可以用方程的方法解决.总之,在复习中要注意领悟蕴含在知识和解题过程中函数和方程的思想,用它来指导解题.在解题中,同时要注意从不同的角度去观察探索,寻求多种方法,从而得到最佳解题方案.
一、例题分析
例1.已知F(x)=xα-xβ在x∈(0,1)时函数值为正数,试比较α,β的大小.
分析:一般情况下,F(x)可以看成两个幂函数的差.已知函数值为正数,即f1(x)=xα的图象在x∈(0,1)上位于f2(x)=xβ的图象的上方,这时为了判断幂指数α,β的大小,就需要讨论α,β的值在(1,+∞)上,或是在(0,1)上,或是在(0,1)内的常数,于是F(x)成为两个同底数指数函数之差,由于指数函数y=at(0<α<1)是减函数,又因为xα-xβ>0,所以得α<β.
例2.已知0<a<1,试比较![]() 的大小.
的大小.
分析:为比较aα与(aα) α的大小,将它们看成指数相同的两个幂,由于幂函数![]() 在区间[0,+∞]上是增函数,因此只须比较底数a与aα的大小,由于指数函数y=ax(0<a<1)为减函数,且1>a,所以a<aα,从而aα<(aα) α.
在区间[0,+∞]上是增函数,因此只须比较底数a与aα的大小,由于指数函数y=ax(0<a<1)为减函数,且1>a,所以a<aα,从而aα<(aα) α.
比较aα与(aα) α的大小,也可以将它们看成底数相同(都是aα)的两个幂,于是可以利用指数函数 ![]() 是减函数,由于1>a,得到aα<(aα) α.
是减函数,由于1>a,得到aα<(aα) α.
由于a<aα,函数y=ax(0<a<1)是减函数,因此aα>(aα) α.
综上, ![]()
![]() .
.
解以上两个例题的关键都在于适当地选取某一个函数,函数选得恰当,解决问题简单.
例3.关于x的方程 ![]() 有实根,且根大于3,求实数a的范围.
有实根,且根大于3,求实数a的范围.
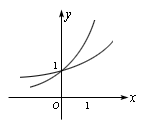
分析:先将原方程化简为ax=3,但要注意0<x<3且x≠1.现将ax看成以a为底的指数函数,考虑底数a为何值时,函数值为3.如图(1),过(3,3)点的指数函数的底 ![]() ,现要求0<x<3时,ax=3,所以
,现要求0<x<3时,ax=3,所以 ![]() ,又因为x≠1,在图(1)中,过(1,3)点的指数函数的底a=3,所以
,又因为x≠1,在图(1)中,过(1,3)点的指数函数的底a=3,所以 ![]() .
.
若将ax=3变形为 ![]() ,令
,令 ![]() ,现研究指数函数a=3t,由0<x<1且x≠1,得
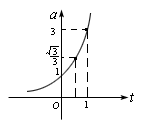
,现研究指数函数a=3t,由0<x<1且x≠1,得 ![]() ,如图(2),很容易得到:
,如图(2),很容易得到: ![]() .
.
通过本例,说明有些问题可借助函数来解决,函数选择得当,解决就便利.
例4.函数f(x)是定义在实数集上的周期函数,且是偶函数,已知当x∈[2,3]时,f(x)=x,则当x∈[-2,0]时,f(x)的解析式是( ).
(A)f(x)=x+4
(B)f(x)=2-x
(C)f(x)=3-x+1 (D)f(x)=3+x+1
解法一、∵f(-2)=f(2)=2 f(-1)=f(3)=3,∴只有(A)、(C)可能正确.
又∵f(0)=f(2)=2,∴(A)错,(C)对,选(C).
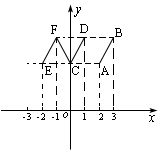
解法二、依题意,在区间[2,3]上,函数的图象是线段AB,
∵函数周期是2,
∴线段AB左移两个单位得[0,1]上的图象线段CD;再左移两个单位得[–2,1]上的图象线段EF .
∵函数是偶函数,
∴把线段CD沿y轴翻折到左边,得[–1,0]上的图象线段FC.
于是由直线的点斜式方程,得函数在[–2,0]上的解析式:
![]()
![]()
即![]()
![]()
由于x∈[-2,-1]时,x+1≤0,x∈(-1,0)时,x+1>0, 所以y=3-x+1, x∈[-2,0].
解法三、当x∈[-2,-1]时,x+4∈[2,3],
∵函数周期是2,
∴f(x+4)=f(x).
而f(x+4)=x+4,
∴x∈[-2,-1]时,f(x)=x+4=3+(x+1).
当x∈[-1,0]时,-x∈[0,1],
且-x+2∈[2,3].
∵函数是偶函数,周期又是2,
∴![]() ,
,
于是在[–2,0]上, ![]()
![]() .
.
由于x∈[-2,-1]时,x+1≤0,x∈(-1,0)时,x+1>0,
根据绝对值定义有x∈[-2,0]时,f(x)=3-x+1.
本题应抓住“偶函数”“周期性”这两个概念的实质去解决问题.
例5.已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是( ).
(A)(0,1) (B)(1,2) (C)(0,2) (D)[2,+∞]
分析:设t=2-ax,则y=logat,
因此,已知函数是上面这两个函数的复合函数,其增减性要考查这两个函数的单调性,另外,还要考虑零和负数无对数以及参数a对底数和真数的制约作用.
解法一、由于a≠1,所以(C)是错误的.
又a=2时,真数为2–2x,于是x≠1,这和已知矛盾,所以(D)是错的.
当0<a<1时,t=2-ax是减函数,而y=logat也是减函数,
故y=loga(2-ax)是x的增函数,所以(A)是错的.
于是应选(B).
解法二、设t=2-ax,y=logat
由于a>0,所以t=2-ax是x的减函数,
因此,只有当a>1,y=logat是增函数时,y=loga(2-ax)在[0,1]上才是减函数;
又x=1时,y=loga(2-a),
依题意,此时,函数有定义,故2–a>0
综上可知:1<a<2,
故应选(B).
例6.已知![]() ,函数y=g(x)的图象与函数y=f-1(x+1)的图象关于y’=x对称,则g(5)=_____________-
,函数y=g(x)的图象与函数y=f-1(x+1)的图象关于y’=x对称,则g(5)=_____________-
解法一、由![]() 去分母,得
去分母,得![]() ,解出x,得
,解出x,得![]() ,
,
故![]() ,于是
,于是![]() ,
,
设![]() ,去分母得,
,去分母得,![]() ,解出x,得
,解出x,得![]() ,
,
∴![]() 的反函数
的反函数![]() .
.
∴![]() .
.
解法二、由![]() ,则
,则![]() ,
,
∴![]() ,∴
,∴![]() .
.
即![]() 的反函数为
的反函数为![]() ,
, 
根据已知:![]()
∴![]() .
.
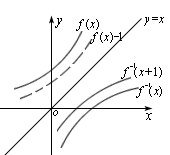
解法三、如图,f(x)和f-1(x)互为反函数,当f-1(x)的图象沿x轴负方向平移一个单位时,做为“镜面”的另一侧的“象”f(x)的图象一定向下平移1个单位,因此f-1(x+1)的图象与f(x)-1的图象关于y=x对称.
故f-1(x+1)的反函数是g(x)=f(x)-1,
∴![]() .
.
本解法从图象的运动变化中,探求出f-1(x+1)的反函数,体现了数形结合的优势出
二、巩固练习
(1) 已知函数![]() 在区间
在区间![]() 上的最大值为1,求实数a的值.
上的最大值为1,求实数a的值.
(1)解:f(x)在区间![]() 上最大值可能在端点外取得,也可能在顶点外取得,
上最大值可能在端点外取得,也可能在顶点外取得,![]() ,
,![]() ,而顶点横坐标
,而顶点横坐标![]() ,最大值在顶点外取得,故此解舍去.
,最大值在顶点外取得,故此解舍去.
当最大值为f(2)时,f(2)=1,![]() ,顶点在
,顶点在![]() 应在区间右端点取得最大值,此解合理.
应在区间右端点取得最大值,此解合理.
当最大值在顶点处取得时,由![]() ,解得
,解得![]() ,当
,当![]() ,此时,顶点不在区间
,此时,顶点不在区间![]() 内,应舍去.
内,应舍去.
综上,![]() .
.
(2)函数![]() 的定义域是[a,b],值域也是[a,b],求a.b的值.2)解:y=f(x)的图象如图,分三种情况讨论.
的定义域是[a,b],值域也是[a,b],求a.b的值.2)解:y=f(x)的图象如图,分三种情况讨论.
当a<b≤0时,f(x)为递增函数,有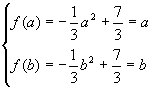 ,
,
解得,![]() ,由于b>0,应舍去.
,由于b>0,应舍去.
当0≤a<b时,f(x)为递减函数,
有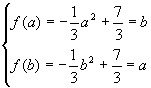 ,解得:a=1,b=2.
,解得:a=1,b=2.
当a<0<b时,f(x)最大值在顶点处取得,故![]() ,
,![]() ,所以最小值应在a处取得. (2)解:y=f(x)的图象如图,分三种情况讨论.
,所以最小值应在a处取得. (2)解:y=f(x)的图象如图,分三种情况讨论.
当a<b≤0时,f(x)为递增函数,有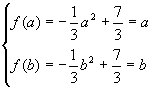 ,
,
解得,![]() ,由于b>0,应舍去.
,由于b>0,应舍去.
当0≤a<b时,f(x)为递减函数,
有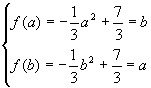 ,解得:a=1,b=2.
,解得:a=1,b=2.
当a<0<b时,f(x)最大值在顶点处取得,故![]() ,
,![]() ,所以最小值应在a处取得.
,所以最小值应在a处取得.
![]() ,解得:
,解得:![]() ,
,
综上,![]() 或
或 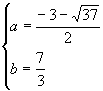
(3)求函数![]() 的最小值. 解(3)分析:由于对数的底已明确是2,所以只须求
的最小值. 解(3)分析:由于对数的底已明确是2,所以只须求![]() 的最小值.
的最小值.
(3)解法一:∵![]() ,∴x>2.
,∴x>2.
设![]() ,则
,则![]() ,
,
由于该方程有实根,且实根大于2,
∴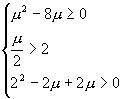 解之,μ≥8.
解之,μ≥8.
当μ=8时,x=4,故等号能成立.
于是log2≥0且x=4时,等号成立,因此![]() 的最小值是3.
的最小值是3.
解法二:∵![]() ,∴x>2
,∴x>2
设![]() ,则
,则![]() =
=![]()
![]()
∴μ≥8且![]() ,即x=4时,等号成立,
,即x=4时,等号成立,
∴log2μ≥3且x=4时,等号成立.
故![]() 的最小值是3.
的最小值是3.
(4)已知a>0,a≠1,试求方程![]() 有解时k的取值范围. 4)解法一:原方程
有解时k的取值范围. 4)解法一:原方程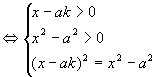
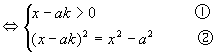
由②可得:![]() ③,
③,
当k=0时,③无解,原方程无解;
当k≠0时,③解为![]() ,代入①式,
,代入①式,![]()
![]() .
.
解法二:原方程![]() ,
,
原方程有解,应方程组
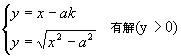 ,
,
即两曲线有交点,那么ak<-a或0<ak<a(a>0)
∴k<-1或0<k<1.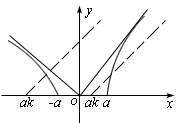
(5)设函数![]()
(Ⅰ)解不等式f(x)≤1
(Ⅱ)求a的取值范围,使f(x)在[0,+∞]上是单调函数.
5)解(Ⅰ),不等式f(x≤1),即![]()
由此得:1≤1+ax即ax≥0,其中常数a>0,
∴原不等式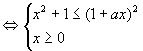 即
即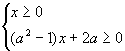
∴当0<a<1时,所给不等式解集为![]() ,
,
当a≥1时,所给不等式解集为{xx≥0}.
(Ⅱ)在区间[0,+∞)上任取x1,x2,使得x1<x2,
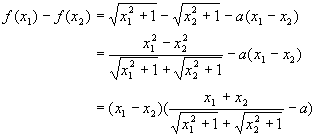
(ⅰ)当a≥1时,
∵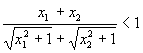
∴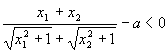
又![]()
∴![]()
所以,当a≥1时,函数f(x)在区间[0,+∞)上是单调递减函数.
(ⅱ)当0<a<1时,在[0,+∞)上存在两点![]() 满足f(x1)=1,f(x2)=1 ,即f(x1)=f(x2),∴函数f(x)在区间[0,+∞)上不是单调函数.
满足f(x1)=1,f(x2)=1 ,即f(x1)=f(x2),∴函数f(x)在区间[0,+∞)上不是单调函数.