第二讲 复习函数
一、 本讲进度
《函数》单元复习
二、 本讲主要内容
1、函数的定义及通性；
2、函数性质的运用。
三、 学习指导
1、函数的概念：
（1）映射：设非空数集A，B，若对集合A中任一元素a，在集合B中有唯一元素b与之对应，则称从A到B的对应为映射，记为f：A→B，f表示对应法则，b=f(a)。若A中不同元素的象也不同，则称映射为单射，若B中每一个元素都有原象与之对应，则称映射为满射。既是单射又是满射的映射称为一一映射。
（2）函数定义：函数就是定义在非空数集A，B上的映射，此时称数集A为定义域，象集C={f(x)x∈A}为值域。定义域，对应法则，值域构成了函数的三要素，从逻辑上讲，定义域，对应法则决定了值域，是两个最基本的因素。逆过来，值域也会限制定义域。
求函数定义域，通过解关于自变量的不等式（组）来实现的。要熟记基本初等函数的定义域，通过四则运算构成的初等函数，其定义域是每个初等函数定义域的交集。复合函数定义域，不仅要考虑内函数的定义域，还要考虑到外函数对应法则的要求。理解函数定义域，应紧密联系对应法则。函数定义域是研究函数性质的基础和前提。
函数对应法则通常表现为表格，解析式和图象。其中解析式是最常见的表现形式。求已知类型函数解析式的方法是待定系数法，抽象函数的解析式常用换元法及凑合法。
求函数值域是函数中常见问题，在初等数学范围内，直接法的途径有单调性，基本不等式及几何意义，间接法的途径为函数与方程的思想，表现为△法，反函数法等，在高等数学范围内，用导数法求某些函数最值（极值）更加方便。
在中学数学的各个部分都存在着求取值范围这一典型问题，它的一种典型处理方法就是建立函数解析式，借助于求函数值域的方法。
2、函数的通性
（1）奇偶性：函数定义域关于原点对称是判断函数奇偶性的必要条件，在利用定义判断时，应在化简解析式后进行，同时灵活运用定义域的变形，如
，
（f(x)≠0）。
奇偶性的几何意义是两种特殊的图象对称。
函数的奇偶性是定义域上的普遍性质，定义式是定义域上的恒等式。
利用奇偶性的运算性质可以简化判断奇偶性的步骤。
（2）单调性：研究函数的单调性应结合函数单调区间，单调区间应是定义域的子集。
判断函数单调性的方法：①定义法，即比差法；②图象法；③单调性的运算性质（实质上是不等式性质）；④复合函数单调性判断法则。
函数单调性是单调区间上普遍成立的性质，是单调区间上恒成立的不等式。
函数单调性是函数性质中最活跃的性质，它的运用主要体现在不等式方面，如比较大小，解抽象函数不等式等。
（3）周期性：周期性主要运用在三角函数及抽象函数中，是化归思想的重要手段。
求周期的重要方法：①定义法；②公式法；③图象法；④利用重要结论：若函数f(x)满足f(a-x)=f(a+x)，f(b-x)=f(b+x)，a≠b，则T=2a-b。
（4）反函数：函数是否是有反函数是函数概念的重要运用之一，在求反函数之前首先要判断函数是否具备反函数，函数f(x)的反函数f-1(x)的性质与f(x)性质紧密相连，如定义域、值域互换，具有相同的单调性等，把反函数f-1(x)的问题化归为函数f(x)的问题是处理反函数问题的重要思想。
设函数f(x)定义域为A，值域为C，则
f-1[f(x)]=x，x∈A
f[f-1(x)]=x，x∈C
3、函数的图象
函数的图象既是函数性质的一个重要方面，又能直观地反映函数的性质，在解题过程中，充分发挥图象的工具作用。
图象作法：①描点法；②图象变换。应掌握常见的图象变换。
4、本单常见的初等函数；一次函数，二次函数，反比例函数，指数函数，对数函数。在具体的对应法则下理解函数的通性，掌握这些具体对应法则的性质。分段函数是重要的函数模型。
对于抽象函数，通常是抓住函数特性是定义域上恒等式，利用赋值法（变量代换法）解题。联系到具体的函数模型可以简便地找到解题思路，及解题突破口。
应用题是函数性质运用的重要题型。审清题意，找准数量关系，把握好模型是解应用题的关键。
5、主要思想方法：数形结合，分类讨论，函数方程，化归等。
四、典型例题
例1、已知
，函数y=g(x)图象与y=f-1(x+1)的图象关于直线y=x对称，求g(11)的值。
解题思路分析：
利用数形对应的关系，可知y=g(x)是y=f-1(x+1)的反函数，从而化g(x)问题为已知f(x)。
∵ y=f-1(x+1)
∴ x+1=f(y)
∴ x=f(y)-1
∴ y=f-1(x+1)的反函数为y=f(x)-1
即 g(x)=f(x)-1
∴ g(11)=f(11)-1=
评注：函数与反函数的关系是互为逆运算的关系，当f(x)存在反函数时，若b=f(a)，则a=f-1(b)。
例2、设f(x)是定义在（-∞，+∞）上的函数，对一切x∈R均有f(x)+f(x+2)=0，当-1<x≤1时，f(x)=2x-1，求当1<x≤3时，函数f(x)的解析式。
解题思路分析：
利用化归思想解题
∵ f(x)+f(x+2)=0
∴ f(x)=-f(x+2)
∵ 该式对一切x∈R成立
∴ 以x-2代x得：f(x-2)=-f[(x-2)+2]=-f(x)
当1<x≤3时，-1<x-2≤1
∴ f(x-2)=2(x-2)-1=2x-5
∴ f(x)=-f(x-2)=-2x+5
∴ f(x)=-2x+5（1<x≤3）
评注：在化归过程中，一方面要转化自变量到已知解析式的定义域，另一方面要保持对应的函数值有一定关系。在化归过程中还体现了整体思想。
例3、已知g(x)=-x2-3，f(x)是二次函数，当x∈[-1，2]时，f(x) 的最小值，且f(x)+g(x)为奇函数，求f(x)解析式。
解题思路分析：
用待定系数法求f(x)解析式
设f(x)=ax2+bx+c（a≠0）
则f(x)+g(x)=(a-1)x2+bx+c-3
由已知f(x)+g(x)为奇函数
∴ 
∴ f(x)=x2+bx+3
下面通过确定f(x)在[-1，2]上何时取最小值来确定b，分类讨论。
，对称轴
（1）
当
≥2，b≤-4时，f(x)在[-1，2]上为减函数
∴ 
∴ 2b+7=1
∴ b=3（舍）
（2）
当
（-1，2），-4<b<2时
∴ 
∴ 
（舍负）
（3）
当≤-1，b≥2时，f(x)在[-1，2]上为增函数
∴ (f(x)min=f(1)=4-b
∴ 4-b=1
∴ b=3
∴ 
，或
评注：二次函数在闭区间上的最值通常对对称轴与区间的位置关系进行讨论，是求值域的基本题型之一。在已知最值结果的条件下，仍需讨论何时取得最小值。
例4、定义在R上的函数y=f(x)，f(0)≠0，当x>0时，f(x)>1，且对任意的a、b∈R，有f(a+b)=f(a)f(b)，
（1） 求证：f(0)=1；
（2） 求证：对任意的x∈R，恒有f(x)>0；
（3） 证明：f(x)是R上的增函数；
（4） 若f(x)·f(2x-x2)>1，求x的取值范围。
解题思路分析：
（1） 令a=b=0，则f(0)=[f(0)]2
∵ f(0)≠0
∴ f(0)=1
（2） 令a=x，b=-x
则 f(0)=f(x)f(-x)
∴ 
由已知x>0时，f(x)>1>0
当x<0时，-x>0，f(-x)>0
∴ 
又x=0时，f(0)=1>0
∴ 对任意x∈R，f(x)>0
（3） 任取x2>x1，则f(x2)>0，f(x1)>0，x2-x1>0
∴ 
∴ f(x2)>f(x1)
∴ f(x)在R上是增函数
（4） f(x)·f(2x-x2)=f[x+(2x-x2)]=f(-x2+3x)
又1=f(0)，f(x)在R上递增
∴ 由f(3x-x2)>f(0)得：3x-x2>0
∴ 0<x<3
评注：根据f(a+b)=f(a)·f(b)是恒等式的特点，对a、b适当赋值。利用单调性的性质去掉符号“f”得到关于x的代数不等式，是处理抽象函数不等式的典型方法。
例5、已知lgx+lgy=2lg(x-2y)，求
的值。
解题思路分析：
在化对数式为代数式过程中，全面挖掘x、y满足的条件
由已知得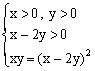
∴ x=4y，
∴ 
例6、某工厂今年1月，2月，3月生产某产品分别为1万件，1.2万件，1.3万件，为了估测以后每个月的产量，以这三个月的产品数量为依据，用一个函数模拟该产品的月产量y与月份数x的关系，模拟函数可选用y=abx+c（其中a，b，c为常数）或二次函数，已知4月份该产品的产量为1.37万件，请问用哪个函数作为模拟函数较好？并说明理由。
解题思路分析：
设f(x)=px2+qx+r（p≠0）
则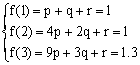 
∴ 
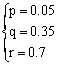
∴ f(4)=-0.05×42+0.35×4+0.7=1.3
设g(x)=abx+c
则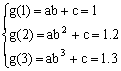 
∴ 
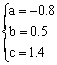
∴ g(4)=-0.8×0.54+1.4=1.35
∵ 1.35-1.37<1.3-1.37
∴ 选用y=-0.8×(0.5)x+1.4作为模拟函数较好。
五、同步练习
（一） 选择题
1、定义在R上的偶函数f(x)满足f(x+1)=-f(x)，且在[-1，0]上单调递增，设a=f(3)，b=f(
)，c=f(2)，则a，b，c大小关系是
A、a>b>c B、a>c>b C、b>c>a D、c>b>a
2、方程
（a>0且a≠1）的实数解的个数是
A、0 B、1 C、2 D、3
3、
的单调减区间是
A、（-∞，1） B、（1，+∞） C、（-∞，-1）∪（1，+∞） D、（-∞，+∞）
4、函数
的值域为
A、 （-∞，3] B、（-∞，-3] C、（-3，+∞） D、（3，+∞）
5、函数y=log2ax-1（a≠b）的图象的对称轴是直线x=2，则a等于
A、 
B、
C、2
D、-2
6、有长度为24的材料用一矩形场地，中间加两隔墙，要使矩形的面积最大，则隔壁的长度为
A、 3 B、4 C、6 D、12
（二） 填空题
7、已知定义在R的奇函数f(x)满足f(x+2)=-f(x)，且当0≤x≤1时，f(x)=x，则
=__________。
8、 已知y=loga(2-x)是x的增函数，则a的取值范围是__________。
9、 函数f(x)定义域为[1，3]，则f(x2+1)的定义域是__________。
10、函数f(x)=x2-bx+c满足f(1+x)=f(1-x)，且f(0)=3，则f(bx)与f(cx)的大小关系是__________。
11、已知f(x)=log3x+3，x∈[1，9]，则y=[f(x)]2+f(x2)的最大值是__________。
12、已知A={yy=x2-4x+6，y∈N}，B={yy=-x2-2x+18，y∈N}，则A∩B中所有元素的和是__________。
13、若φ(x)，g(x)都是奇函数，f(x)=mφ(x)+ng(x)+2在（0，+∞）上有最大值，则f(x)在（-∞，0）上最小值
为__________。
14、函数y=log2(x2+1)（x>0）的反函数是__________。
15、求值：
=__________。
（三） 解答题
16、若函数
的值域为[-1，5]，求a，c。
17、设定义在[-2，2]上的偶函数f(x)在区间[0，2]上单调递减，若f(1-m)<f(m)，求实数m的取值范围。
18、已知0<a<1，在函数y=logax（x≥1）的图象上有A，B，C三点，它们的横坐标分别是t，t+2，t+4
（1） 若△ABC面积为S，求S=f(t)；
（2） 判断S=f(t)的单调性；
（3） 求S=f(t)最大值。
19、设f(x)=
，x∈R
（1） 证明：对任意实数a，f(x)在（-∞，+∞）上是增函数；
（2） 当f(x)为奇函数时，求a；
（3）
当f(x)为奇函数时，对于给定的正实数k，解不等式
。
20、设0<a<1，函数f(x)=
的定义域为[m，n]，值[logaa(n-1)，logaa(m-1)]，
（1） 求证：m>3；
（2） 求a的取值范围。
参考答案
（一） 选择题
1、 D 2、B 3、B 4、B 5、A 6、A
（二） 填空题
7、
8、（0，1） 9、[
] 10、f(bx)≤f(cx) 11、13
12、
189 13、-1 14、
（x>0） 15、1
（三） 解答题
16、
17.[-1，]
18、（1）
（t≥1）
（2）在[1，+∞）上是减函数
（3）t=1时，
19、（1）a=1；
（2）当0<k≤2时，1-k<x<1；当k>2时，-1<x<1
20、