08届高考调理科数学调研考试试题
2008.2.19
本卷分选择题和非选择题两部分,满分150分.考试用时间120分钟.
注意事项:
1. 考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答题卷上;
2. 选择题、填空题每小题得出答案后,请将答案填写在答题卷相应指定位置上。答在试题卷上不得分;
3. 考试结束,考生只需将答题案交回。
参考公式:锥体的体积公式![]() ,其中
,其中![]() 是锥体的底面积,
是锥体的底面积,![]() 是锥体的高.
是锥体的高.
如果事件![]() 、
、![]() 互斥,那么
互斥,那么![]() .
.
如果事件![]() 、
、![]() 相互独立,那么
相互独立,那么![]() .
.
第一部分 选择题(共40分)
一、选择题(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 已知复数![]() ,则
,则![]()
A. ![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
2. 设全集![]() 且
且![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 椭圆![]() 的焦点在
的焦点在![]() 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C. 2 D.4
C. 2 D.4
4. ![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]()
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
5. 已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,则过点
,则过点![]() 和
和![]()
![]() N*)的直线的斜率是
N*)的直线的斜率是
A.4 B.3 C.2 D.1
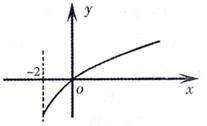 6.已知函数
6.已知函数![]() ,且
,且![]() ,
,![]() 的导函数,函数
的导函数,函数![]() 的图象如图所示. 则平面区域
的图象如图所示. 则平面区域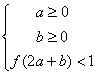 所围成的面积是
所围成的面积是
A.2 B.4 C.5 D.8
7. 一台机床有![]() 的时间加工零件A, 其余时间加工零件B, 加工A时,停机的概率是
的时间加工零件A, 其余时间加工零件B, 加工A时,停机的概率是![]() ,
,
加工B时,停机的概率是![]() , 则这台机床停机的概率为( )
, 则这台机床停机的概率为( )
A.
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8.
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数![]() 的图象恰好通过
的图象恰好通过![]() 个整点,则称函数
个整点,则称函数![]() 为
为![]() 阶整点函数。有下列函数:
阶整点函数。有下列函数:
① ![]() ; ②
; ②![]() ③
③![]() ④
④![]() ,
,
其中是一阶整点函数的是( )
A.①②③④ B.①③④ C.①④ D.④
第二部分 非选择题(共110分)
二.填空题(每小题5分,共30分)
 9. 若奇函数
9. 若奇函数![]() 的定义域为
的定义域为![]() ,则
,则![]() =
=
10. 计算![]()
11.已知正三角形内切圆的半径是高的![]() ,把这个结论推广到空间正四面体,类似的结论是____________________.
,把这个结论推广到空间正四面体,类似的结论是____________________.
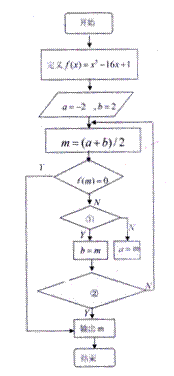
12.右图是用二分法求方程![]() 在
在![]() 的近似解的程序框图,要求解的精确度为
的近似解的程序框图,要求解的精确度为![]() ,①处填的内容是____________, ②处填的内容是______________________.
,①处填的内容是____________, ②处填的内容是______________________.
第13至15题,从3题中选答2题,多选按前2题记分
13. 设M、N分别是曲线![]() 和
和![]() 上的动点,则M、N的最小距离是
上的动点,则M、N的最小距离是
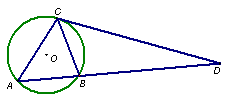
14. 如图,圆![]() 是
是![]() 的外接圆,过点C的切线交
的外接圆,过点C的切线交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() 。则
。则![]() 的长______________,
的长______________,![]() 的长______________.
的长______________.
 15. 已知
15. 已知![]() 且
且![]() ,
,
则![]() .
.
16.(本题满分12分)
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() …
…![]() 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
 (Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和
平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,
求他们在同一分数段的概率.
17.(本题满分12分)
已知![]()
![]() ,
,
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ) 当![]() ,求函数
,求函数![]() 的零点.
的零点.
18. (本题满分14分)
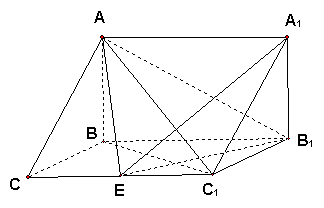
如图,在三棱拄![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]()
![]()
(Ⅰ)求证:![]() ;
;
(Ⅱ)试在棱![]() (不包含端点
(不包含端点![]() 上确定一点
上确定一点![]() 的位置,使得
的位置,使得![]() ;
;
(Ⅲ) 在(Ⅱ)的条件下,求二面角![]() 的平面角的正切值.
的平面角的正切值.
19. (本题满分14分)
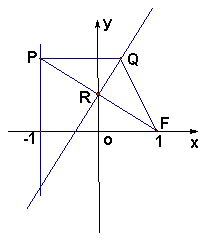
在平面直角坐标系![]() 中,设点
中,设点![]() (1,0),直线
(1,0),直线![]() :
:![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动,![]() 是线段
是线段![]() 与
与![]() 轴的交点,
轴的交点, ![]() .
.
 (Ⅰ)求动点
(Ⅰ)求动点![]() 的轨迹的方程;
的轨迹的方程;
(Ⅱ) 记![]() 的轨迹的方程为
的轨迹的方程为![]() ,过点
,过点![]() 作两条互相垂直的曲线
作两条互相垂直的曲线![]() 的弦
的弦![]() 、
、![]() ,设
,设![]() 、
、![]() 的中点分别为
的中点分别为![]() .求证:直线
.求证:直线![]() 必过定点
必过定点![]() .
.
20.(本题满分14分)
已知数列![]() 中,
中,![]() ,且
,且![]()
(Ⅰ)求证:![]()
![]() ;
;
(Ⅱ)设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,求
项和,求![]() 的解析式;
的解析式;
(Ⅲ)求证:不等式![]() 对
对![]() 恒成立.
恒成立.
21. (本题满分14分)已知函数![]() (其中
(其中![]() ) ,
) ,
点![]() 从左到右依次是函数
从左到右依次是函数![]() 图象上三点,且
图象上三点,且![]() .
.
(Ⅰ) 证明: 函数![]() 在
在![]() 上是减函数;
上是减函数;
(Ⅱ)
求证:⊿![]() 是钝角三角形;
是钝角三角形;
(Ⅲ) 试问,⊿![]() 能否是等腰三角形?若能,求⊿
能否是等腰三角形?若能,求⊿![]() 面积的最大值;若不能,请说明理由.
面积的最大值;若不能,请说明理由.
08届高考调理科数学调研考试试题答案及评分标准
一、选择题 CCABA BAC
二、填空题
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
| 6 |
|
|
| 4, | 1 |
三、解答题
 16.(本题满分12分)
16.(本题满分12分)
(Ⅰ)因为各组的频率和等于1,故第四组的频率:
![]() ……2分
……2分
直方图如右所示……………………………….4分
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为 ![]()
所以,抽样学生成绩的合格率是![]() %......................................6分
%......................................6分
利用组中值估算抽样学生的平均分
![]() ………………….8分
………………….8分
=![]()
=71
估计这次考试的平均分是71分………………………………………….9分
(Ⅲ)![]() ,
,![]() ,
,![]() ”的人数是18,15,3。所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
”的人数是18,15,3。所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
![]()
![]() ……………………………………………………12分
……………………………………………………12分
17.(本题满分12分)
解:(Ⅰ)![]() =
=![]() …………………….4分
…………………….4分
故![]() …………………………………………………5分
…………………………………………………5分
(Ⅱ)令![]() ,
,![]() =0,又
=0,又![]()
![]() …… ………….7分
…… ………….7分
![]()
![]() …………………………………………9分
…………………………………………9分
故![]() 函数
函数![]() 的零点是
的零点是![]() ……………. 12分
……………. 12分
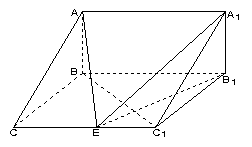
18.(本题满分12分)
证(Ⅰ)因为![]() 侧面
侧面![]() ,故
,故![]()
在![]() 中,
中,![]() 由余弦定理有
由余弦定理有
![]()
 故有
故有 ![]()
而 ![]() 且
且![]() 平面
平面![]()
![]()
![]()
(Ⅱ)由![]()
从而![]() 且
且![]() 故
故![]()
不妨设 ![]() ,则
,则![]() ,则
,则![]()
又![]() 则
则![]()
在![]() 中有
中有 ![]() 从而
从而![]() (舍负)
(舍负)
故![]() 为
为![]() 的中点时,
的中点时,![]()
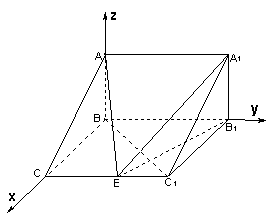 法二:以
法二:以![]() 为原点
为原点![]() 为
为![]() 轴,设
轴,设![]() ,则
,则![]() 由
由![]() 得
得 ![]() 即
即
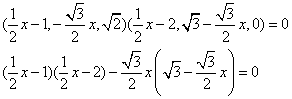
化简整理得 ![]()
![]() 或
或 ![]()
当![]() 时
时![]() 与
与![]() 重合不满足题意
重合不满足题意
当![]() 时
时![]() 为
为![]() 的中点
的中点
故![]() 为
为![]() 的中点使
的中点使![]()
(Ⅲ)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]()
连![]() 则
则![]() ,连
,连![]() 则
则![]() ,连
,连![]() 则
则![]()
连![]() 则
则![]() ,且
,且![]() 为矩形,
为矩形,![]()
又![]() 故
故![]() 为所求二面角的平面角
为所求二面角的平面角
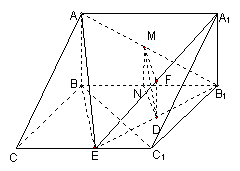 在
在![]() 中,
中,![]()
![]()
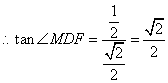
法二:由已知![]() , 所以二面角
, 所以二面角![]() 的平面角
的平面角![]() 的大小为向量
的大小为向量![]() 与
与![]() 的夹角
的夹角
因为![]()
![]()
故 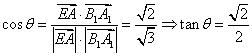
.
19. (本题满分14分)
 解:(Ⅰ)依题意知,直线
解:(Ⅰ)依题意知,直线![]() 的方程为:
的方程为:![]() .点
.点![]() 是线段
是线段![]() 的中点,且
的中点,且![]() ⊥
⊥![]() ,∴
,∴![]() 是线段
是线段![]() 的垂直平分线.…………………….2分
的垂直平分线.…………………….2分
∴![]() 是点
是点![]() 到直线
到直线![]() 的距离.
的距离.
∵点![]() 在线段
在线段![]() 的垂直平分线,∴
的垂直平分线,∴![]() .…………4分
.…………4分
故动点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点,
为焦点,![]() 为准线的抛物线,其方程为:
为准线的抛物线,其方程为:![]() .…………………………………………………….7分
.…………………………………………………….7分
(Ⅱ) 设![]() ,
,![]() ,直线AB的方程为
,直线AB的方程为![]()
…………………………………………………….8分
则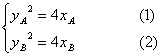
(1)—(2)得![]() ,即
,即![]() ,……………………………………9分
,……………………………………9分
代入方程![]() ,解得
,解得![]() .
.
所以点M的坐标为![]() .……………………………………10分
.……………………………………10分
同理可得:![]() 的坐标为
的坐标为![]() .
.
直线![]() 的斜率为
的斜率为![]() ,方程为
,方程为
![]() ,整理得
,整理得![]() ,………………12分
,………………12分
显然,不论![]() 为何值,
为何值,![]() 均满足方程,
均满足方程,
所以直线![]() 恒过定点
恒过定点![]()
![]() .………………14
.………………14
20. (本题满分14分)
.解:![]()
故![]() ,.……………………………………1分
,.……………………………………1分
又因为![]()
则![]()
![]() ,即
,即![]() .………………………3分
.………………………3分
所以![]() , ……………………………………4
, ……………………………………4
(2)
![]()
![]() =
=![]() ……………………………………6
……………………………………6
因为![]() =
=![]()
所以,当![]() 时,
时,![]() ……………………………7
……………………………7
当![]() 时,
时,![]() ……….(1)
……….(1)
![]() 得
得![]() ……(2)
……(2)
![]()
=![]()
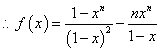 ……………………………9
……………………………9
综上所述: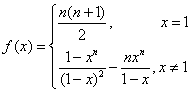 ……………………………10
……………………………10
(3)因为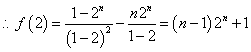
又![]() ,易验证当
,易验证当![]() ,3时不等式不成立; ……………………………11
,3时不等式不成立; ……………………………11
假设![]() ,不等式成立,即
,不等式成立,即![]()
两边乘以3得:![]()
又因为![]()
所以![]()
即![]() 时不等式成立.故不等式恒成立.
……………………………14
时不等式成立.故不等式恒成立.
……………………………14
21. (本题满分14分)
解:(Ⅰ) ![]()
![]() …………………………
…………………………
所以函数![]() 在
在![]() 上是单调减函数.
上是单调减函数.![]() …………………………4分
…………………………4分
(Ⅱ)
证明:据题意![]() 且x1<x2<x3,
且x1<x2<x3,
由(Ⅰ)知f
(x1)>f (x2)>f (x3), x2=![]() …………………………6分
…………………………6分
![]()
![]() …………………8分
…………………8分
![]()
![]()
即⊿![]() 是钝角三角形……………………………………..9分
是钝角三角形……………………………………..9分
(Ⅲ)![]() 假设⊿
假设⊿![]() 为等腰三角形,则只能是
为等腰三角形,则只能是![]()
![]() 即
即![]()
![]()
![]()
![]()
![]()
![]() ①
…………………………………………..12分
①
…………………………………………..12分
而事实上, ![]() ②
②
由于![]() ,故(2)式等号不成立.这与
,故(2)式等号不成立.这与![]() 式矛盾. 所以⊿
式矛盾. 所以⊿![]() 不可能为等腰三角形..14分
不可能为等腰三角形..14分