高考数学第二轮专题复习----解析几何专题

《曲线的方程和性质》专题

一、《考试大纲》要求

⒈直线和圆的方程
　　（1）理解直线的倾斜角和斜率的概念，掌握过两点的直线的斜率公式．掌握直线方　　　　　程的点斜式、两点式、一般式，并能根据条件熟练地求出直线方程．
　　（2）掌握两条直线平行与垂直的条件，两条直线所成的角和点到直线的距离公式．能够根据直线的方程判断两条直线的位置关系．
　　（3）了解二元一次不等式表示平面区域．
　　（4）了解线性规划的意义，并会简单的应用．
　　（5）了解解析几何的基本思想，了解坐标法．
　　（6）掌握圆的标准方程和一般方程，了解参数方程的概念，理解圆的参数方程．
⒉圆锥曲线方程
　　（1）掌握椭圆的定义、标准方程和椭圆的简单几何性质，理解椭圆的参数方程．
　　（2）掌握双曲线的定义、标准方程和双曲线的简单几何性质．
　　（3）掌握抛物线的定义、标准方程和抛物线的简单几何性质．
　　（4）了解圆锥曲线的初步应用．
二、高考试题回放

1．（福建）已知F₁、F₂是椭圆的两个焦点，过F₁且与椭圆长轴垂直的直线交椭圆于A、B两点，若△ABF₂是正三角形，则这个椭圆的离心率是　　　　　　　　　  （　　）

A．　　　　　B．　 　　　 C．　　　　　D．

2．(福建)直线x+2y=0被曲线x²+y²－6x－2y－15=0所截得的弦长等于　　　　　  .

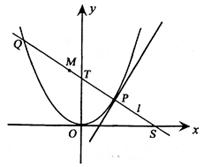3．（福建）如图，P是抛物线C：y=x²上一点，直线l过点P且与抛物线C交于另一点Q.（Ⅰ）若直线l与过点P的切线垂直，求线段PQ中点M的轨迹方程；

（Ⅱ）若直线l不过原点且与x轴交于点S，与y轴交于点T，试求的取值范围.

4．（湖北）已知点M（6，2）和M₂（1，7）.直线y=mx—7与线段M₁M₂的交点M分有向线段M₁M₂的比为3：2，则m的值为　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　　　 C．　　　　　　　　　　　D．4

5.（湖北）两个圆的公切线有且仅有　　　　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．1条　　　　　　　　　　B．2条　　　　　　　　　　　C．3条　　　　　　　　　　D．4条

6．（湖北）直线的右支交于不同的两点A、B.

（Ⅰ）求实数k的取值范围；

（Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？若存在，求出k的值；若不存在，说明理由.

7．（湖南）如果双曲线上一点P到右焦点的距离为, 那么点P到右准线的距离是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

　　　 A．　　　　　　　　　　 B．13　　　　　　　　　　　 C．5　　　　　　　　　　　　D．

8．（湖南）F₁，F₂是椭圆C：的焦点，在C上满足PF₁⊥PF₂的点P的个数为__________.

9．（湖南）如图，过抛物线x²=4y的对称轴上任一点P（0,m）(m>0)作直线与抛物线交于A,B两点，点Q是点P关于原点的对称点。

（I）设点P分有向线段所成的比为，证明:

（II）设直线AB的方程是x-2y+12=0，过A,B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程.

10.（广东）若双曲线的焦点到它相对应的准线的距离是2，则k= 　　　

　　A． 6　　　　  　　　B． 8　　　　　　　 C． 1　　　　 　　　　D． 4

11．（广东）如右下图,定圆半径为 ( b ,c ), 则直线ax+by+c=0

与直线 x–y+1=0的交点在(　　)

　A．第四象限　　　　　　　　　　　　　　　　　　 B． 第三象限　　

　 C．第二象限　　　　　　　　　　　　 D、第一象限

12．（广东）设直线与椭圆相交于A、B两点，又与双曲线x²–y²=1相交于C、D两点， C、D三等分线段AB． 求直线的方程.

13．(江苏)若双曲线的一条准线与抛物线的准线重合，则双曲线的离心率为　　　　　　　　　　　　　　　　　　　　　　　　  （　　）

　　　A．　　　　 　　　B．　　　　 　C． 4　　　　　 　　 D．

14、(江苏)以点(1，2)为圆心，与直线4x+3y-35=0相切的圆的方程是________________.

15．(江苏)制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目. 根据预测，甲、乙项目可能的最大盈利率分别为100﹪和50﹪，可能的最大亏损率分别为30﹪和10﹪. 投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？

16.(江苏)已知椭圆的中心在原点，离心率为，一个焦点是F（-m,0）(m是大于0的常数).　　

 (Ⅰ)求椭圆的方程；　

 (Ⅱ)设Q是椭圆上的一点，且过点F、Q的直线与y轴交于点M. 若，求直线的斜率.

17、（辽宁）已知点、，动点P满足. 当点P的纵坐标是时，点P到坐标原点的距离是　　　　　　　　　　　　　　　　　  （　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　　　　C．　　　　　　　　　　D．2

18、（辽宁）若经过点P（－1，0）的直线与圆相切，则此直线在y轴上的截距是　　　　　　　 .

19、（辽宁）设椭圆方程为，过点M（0，1）的直线l交椭圆于点A、B，O是坐标原点，点P满足，点N的坐标为，当l绕点M旋转时，求：　 （1）动点P的轨迹方程；　 （2）的最小值与最大值.

20．（上海）设抛物线的顶点坐标为(2,0),准线方程为x=－1,则它的焦点坐标为　　　 .

21．（上海）圆心在直线x=2上的圆C与y轴交于两点A(0, －4),B(0, －2),则圆C的方程为　　　　　 　　　　　　.

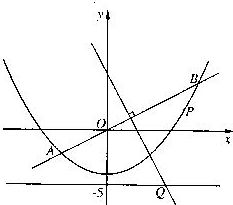
22、（上海）如图, 直线y=x与抛物线y=x²－4交于A、B两点, 线段AB的垂直平分线与直线y=－5交于Q点.

(1) 求点Q的坐标；(2) 当P为抛物线上位于线段AB下方(含A、B) 的动点时, 求ΔOPQ面积的最大值.

23．（重庆）圆的圆心到直线的距离为（　　 ）

　　A．2  B.  C．1　D．

24．（重庆）已知双曲线的左，右焦点分别为,点P在双曲线的右支上，且,则此双曲线的离心率e的最大值为（　　）

　　　　　　　　　　　　　　　　　　　 A．　　　 　　　 B．　　　　　　　 C．　　　　 　D．

25、（重庆）设直线与抛物线交于相异两点A、B，以线段AB为直经作圆H（H为圆心）. 试证抛物线顶点在圆H的圆周上；并求a的值，使圆H的面积最小.

26．（河南）椭圆的两个焦点为F₁、F₂，过F₁作垂直于轴的直线与椭圆相交，一个交点为P，则= 　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　　　C．　　　　　　　　　　　D．4

27、（河南）设抛物线的准线与轴交于点Q，若过点Q的直线与抛物线有公共点，则直线的斜率的取值范围是　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　B．[－2，2]　　　　　　 C．[－1，1]　　　　　　 D．[－4，4]

28、（河南）由动点P向圆x²+y²=1引两条切线PA、PB，切点分别为A、B，∠APB=60°，则动点P的轨迹方程为　　　　　　　　　  .

29、（河南）设双曲线C：相交于两个不同的点A、B.（I）求双曲线C的离心率e的取值范围：

（II）设直线l与y轴的交点为P，且求a的值.

30．（四川）已知圆C与圆关于直线对称，则圆C的方程为（　　）

　　　 A．　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　 D．

31、（四川）在坐标平面内，与点A（1，2）距离为1，且与点B（3，1）距离为2的直线（　　）

　　　 A．1条　　　　　　　　　　B．2条　　　　　　　　　　C．3条　　　　　　　　　　D．4条

32、（四川）．设中心在原点的椭圆与双曲线=1有公共的焦点，且它们的离心率互为倒数，则该椭圆的方程是　　　　　　　　　  .

33、（四川）给定抛物线C：y²=4x，F是C的焦点，过点F的直线l与C相交于A、B两点。 （Ⅰ）设l的斜率为1，求与的夹角的大小；

（Ⅱ）设，若λ∈[4,9]，求l在y轴上截距的变化范围.

34．（宁夏）过点（－1，3）且垂直于直线的直线方程为　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　D．

35．（宁夏）已知椭圆的中心在原点，离心率，且它的一个焦点与抛物线的焦点重合， 则此椭圆方程为　　　　　　　　　　　　　　　　　　　　　 （　　）

A．　　　B．　　C．　　　　　　D．

 

36．（宁夏）设满足约束条件：

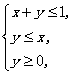
则的最大值是　　　　　　　  .

37．（宁夏）双曲线的焦点距为2c，直线过点（a，0）和（0，b），且点（1，0）到直线的距离与点（－1，0）到直线的距离之和求双曲线的离心率e的取值范围.

三、高考试题分析

1、知识点列表综述

试卷名称	福建	湖北	湖南	广东	江苏
知识点提要	直线与椭圆，椭圆的离心率，直线与圆，直线与抛物线，轨迹方程，变量范围，导数与抛物线结合。	直线方程，线段定比分点坐标，两圆的位置关系，直线与双曲线，双曲线与圆。	双曲线几何性质，椭圆性质，直线与抛物线，线段定比分点，抛物线与圆和向量、导数结合。	双曲线的几何性质，直线与圆，直线与椭圆、双曲线及线段定比分点结合。	双曲线与抛物线的准线，双曲线的离心率，直线与圆相切，线性规划，椭圆方程，直线直线与椭圆，直线的斜率。
试卷名称   知识点提要	辽宁 双曲线定义，直线与圆相切，直线截距，直线与椭圆，与向量结合，轨迹方程，最大值与最小值。	上海 抛物线方程，准线方程，直线和圆，圆的方程，直线与抛物线，对称，最大值。	重庆 直线与圆，双曲线准线，离心率，最大值，直线与圆、抛物线结合、面积最大值。	河南 直线与椭圆、焦点、距离，直线与抛物线的准线、直线斜率的范围，直线与圆、轨迹方程，直线与双曲线、离心率范围、与向量结合。	四川 点到直线距离，直线方程，椭圆与双曲线方程、离心率，直线与抛物线、向量、直线截距范围结合。

2、高考试题的特点：

2.1　题型稳定：近几年来高考解析几何试题一直稳定在1~2个选择题，1个填空题，1个解答题上，分值约为30分， 占总分值的20%左右。

2.2　整体平衡，重点突出：《考试大纲》中解析几何部分有27个知识点，一般考查16 至18 个，其中对直线、线性归划、圆、圆锥曲线等知识的考查几乎没有遗漏，通过对知识的重新组合，考查时既注意全面，更注意突出重点， 对支撑数学科知识体系的主干知识， 考查时保证较高的比例并保持必要深度。

2.3、能力立意，渗透数学思想：如河南第（21）题，将双曲线的方程、性质与坐标法、定比分点的坐标公式、向量、离心率等知识融为一体，有很强的综合性。

2.4、与新教材融合，注意知识的链接：与导数的几何意义、平面向量相结合，与导数结合仅仅停留在对称轴平行于y轴的抛物线上，能与向量结合的试题几乎都联系上。解析几何与函数、方程、不等式等主干知识的结合，几乎各省的解答题都有联系。

2.5、难度下降， 位置不定：近几年解析几何试题的难度有所下降， 选择题、填空题均属易中等题，且解答题不再处于压轴题的位置，计算量减少，思考量增大。

　　3、综合试题的热点问题：

热点之一：圆锥曲线的定义、圆锥曲线方程　圆锥曲线定义是其一切几何性质的“根”与“源”，是建立曲线方程的基础，揭示了圆锥曲线上的点与焦点及准线间的关系，是解几综合题的重要背景。圆锥曲线的方程是研究几何性质的重要载体。

　热点之二：函数与方程的思想 函数与方程的思想是贯穿于解析几何的一条主线，很多解几综合题往往都是以最值问题或圆锥曲线的基本量的求解为依托，通过转化，运用函数与方程的思想加以解决。

　热点之三：与圆锥曲线有关的轨迹问题 解析几何的核心就是用方程的思想研究曲线，用曲线的性质研究方程。轨迹问题正是体现这一思想的重要形式。运用定义法、代入法、参数法、结合问题的几何特征，可以较好的求解。

　热点之四：曲线组合 除了直线和圆锥曲线是传统的结合外，04年的高考题大量出现了圆与双曲线、圆与抛物线、双曲线与抛物线等的结合。

　热点之五：与平面向量、导数等新增内容相结合 利用一切可以利用的机会有机结合。

　热点之六：最值及离心率范围问题 通过求最值及离心率的范围问题达到与函数、方程、不等式等主干知识链接。

四、高考试题展望

高考解析几何的命题一般紧扣课本, 突出重点, 全面考查. 选择题和填空题考查直线, 圆, 圆锥曲线中的基础知识. 解答题重点考查圆锥曲线中的重要知识点, 通过知识的重组与链接, 使知识形成网络, 着重考查直线与圆锥曲线的位置关系, 求解有时还要用到平几的基本知识。

解析几何解答题在历年的高考中常考常新, 体现在重视能力立意, 强调思维空间, 是用活题考死知识的典范. 考题求解时考查了等价转化, 数形结合, 分类讨论, 函数与方程等数学思想, 以及定义法, 配方法, 待定系数法, 参数法, 判别式法等数学通法.

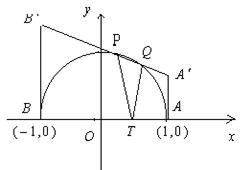
 例1　已知点T是半圆O的直径AB上一点，AB=2、OT=t　(0<t<1)，以AB为直腰作直角梯形，使垂直且等于AT，使垂直且等于BT，交半圆于P、Q两点，建立如图所示的直角坐标系.

(1)写出直线的方程；

　 （2）计算出点P、Q的坐标；

　 （3）证明：由点P发出的光线，经AB反射后，反射光线通过点Q.　　　　　　　　 

 解:  通过读图,　看出点的坐标.

(1 ) 显然,  于是 直线

的方程为；

　 （2）由方程组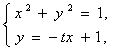

解出　、；　　　　　　　

　 （3）,

　　　  .

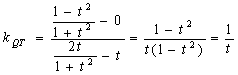　 由直线PT的斜率和直线QT的斜率互为相反数知，由点P发出的光线经点T反射，反射光线通过点Q.

　　　 需要注意的是, Q点的坐标本质上是三角中的万能公式, 有趣吗?

例2　已知直线l与椭圆有且仅有一个交点Q，且与x轴、y轴分别交于R、S，求以线段SR为对角线的矩形ORPS的一个顶点P的轨迹方程．

　 解：从直线所处的位置, 设出直线的方程,

　 由已知，直线l不过椭圆的四个顶点，所以设直线l的方程为

代入椭圆方程 得

　　　　 

化简后，得关于的一元二次方程

　　　　　　

于是其判别式

由已知，得△=0．即　①

在直线方程中，分别令y=0，x=0，求得

 令顶点P的坐标为（x，y），　由已知，得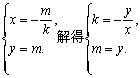

 代入①式并整理，得 ,　即为所求顶点P的轨迹方程．

　　　 方程形似椭圆的标准方程, 你能画出它的图形吗?

　 例3已知双曲线的离心率，过的直线到原点的距离是（1）求双曲线的方程；（2）已知直线交双曲线于不同的点C，D且C，D都在以B为圆心的圆上，求k的值.

解：∵（1）原点到直线AB：的距离.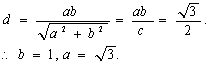

　　 故所求双曲线方程为

（2）把中消去y，整理得 .

　　 设的中点是，则

　　

　 

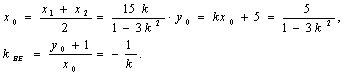
即

故所求k=±.

为了求出的值, 需要通过消元, 想法设法建构的方程.

　 例4 已知椭圆C的中心在原点，焦点F₁、F₂在x轴上，点P为椭圆上的一个动点，且∠F₁PF₂的最大值为90°，直线l过左焦点F₁与椭圆交于A、B两点，△ABF₂的面积最大值为12．

　（1）求椭圆C的离心率；

　（2）求椭圆C的方程．

　 解：（1）设, 对 由余弦定理, 得

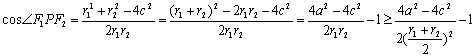
　，解出　

 （2）考虑直线的斜率的存在性，可分两种情况：

　 i) 当k存在时，设l的方程为………………①

　椭圆方程为

 由　 得　 .

于是椭圆方程可转化为　………………②

将①代入②，消去得　　 ,

整理为的一元二次方程，得　　　 .

则x₁、x₂是上述方程的两根．且

，

，

也可这样求解：

AB边上的高

　

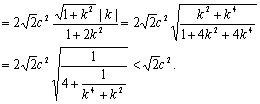
ii) 当k不存在时，把直线代入椭圆方程得

　

由①②知S的最大值为　由题意得=12　所以　　

　故当△ABF₂面积最大时椭圆的方程为：

下面给出本题的另一解法,请读者比较二者的优劣：

设过左焦点的直线方程为：…………①

（这样设直线方程的好处是什么？还请读者进一步反思反思.）

椭圆的方程为：

由得：于是椭圆方程可化为：……②

把①代入②并整理得：

于是是上述方程的两根.

 ,

AB边上的高,

从而

　　　

当且仅当m=0取等号，即

　　由题意知,　于是　.

　　故当△ABF₂面积最大时椭圆的方程为：

　　　例5  已知直线与椭圆相交于A、B两点，且线段AB的中点在直线上.

（１）求此椭圆的离心率；

（2 ）若椭圆的右焦点关于直线的对称点的在圆上，求此椭圆的方程.

　　　解:（1）设A、B两点的坐标分别为 得

,　　

根据韦达定理，得　　　　　 

 ∴线段AB的中点坐标为（）.　

 由已知得

　故椭圆的离心率为 .

 （2）由（1）知从而椭圆的右焦点坐标为 设关于直线的对称点为

解得　 　

由已知得

故所求的椭圆方程为 .

　　　例6 　已知⊙M：轴上的动点，QA，QB分别切⊙M于A，B两点，

　　　（1）如果，求直线MQ的方程；

　　　（2）求动弦AB的中点P的轨迹方程.

　　　解:（1）由，可得由射影定理，得　 在Rt△MOQ中，

　，

　　故，

　　所以直线AB方程是

　　（2）连接MB，MQ，设由

点M，P，Q在一直线上，得

由射影定理得

即 把（*）及（**）消去a，并注意到，可得

　　　适时应用平面几何知识，这是快速解答本题的要害所在，还请读者反思其中的奥妙.

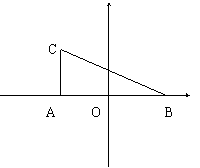
　　例7   如图，在Rt△ABC中，∠CBA=90°，AB=2，AC=。DO⊥AB于O点，OA=OB，DO=2，曲线E过C点，动点P在E上运动，且保持 PA + PB 的值不变.

（1）建立适当的坐标系，求曲线E的方程；

（2）过D点的直线L与曲线E相交于不同的两点M、N且M在D、N之间，设，

　试确定实数的取值范围．

解: （1）建立平面直角坐标系, 如图所示 .　　　　　 

 ∵ PA + PB = CA + CB 　　　　　　　　　　　　　　　  　　　　

　　　=

∴动点P的轨迹是椭圆　　　　　　　　　　　　　　　　　　　　　  　　 

∵　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

∴曲线E的方程是  .

　 （2）设直线L的方程为 , 代入曲线E的方程，得

　　　　

设M₁（,　则

① ② ③

　 　　　　　　　　　　　　　　 

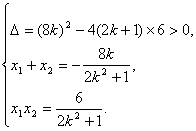
i)  L与y轴重合时，　　　　　　　  　　　　　

ii)  L与y轴不重合时，

  由①得　

  又∵,

∵　或　

∴0＜＜1 ,　　　　　　　　　　　　　　　　  　　　　　　

∴ .　　　　　  　　　

∵

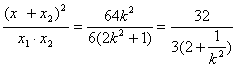
而　∴

∴ 　　　　　　　　　　　　　 

∴ ,　,

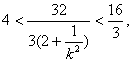
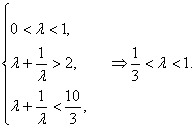　　∴的取值范围是 .　　

　　值得读者注意的是，直线L与y轴重合的情况易于遗漏，应当引起警惕.

　　例8  直线过抛物线的焦点，且与抛物线相交于A两点.

　 （1）求证：;

　 （2）求证：对于抛物线的任意给定的一条弦CD，直线l不是CD的垂直平分线.

　　  　　　　　 

　解: （1）易求得抛物线的焦点.

 若l⊥x轴，则l的方程为.

若l不垂直于x轴，可设,代入抛物线方程整理得 .

综上可知　.

（2）设，则CD的垂直平分线的方程为

假设过F，则整理得

　   

，.

这时的方程为y=0，从而与抛物线只相交于原点. 而l与抛物线有两个不同的交点，因此与l不重合，l不是CD的垂直平分线.

　　　 此题是课本题的深化，你能够找到它的原形吗？知识在记忆中积累，能力在联想中提升. 课本是高考试题的生长点，复习忌忘掉课本！

五、高考复习建议

1、重视教材的基础作用和示范作用

高考试题年年变,但命题的依据是《考试大纲》,要以此为根本,弄清高考的知识点及对基础知识与能力的要求,这中间实质性的工作就是精通课本,客观题一般直接来源于课本，往往是课本的原题或变式题,解析几何的主观试题的生长点也是课本,所以在复习中要精通课本,贯彻“源于课本,高于课本”的原则.在二轮复习选题时，客观题可以根据课本题改变，加强知识点的覆盖，同时还要注意知识的综合。

2、突出“曲线与方程”这一重点内容.

解析几何有两个主要问题,一是由曲线求方程;二是由方程研究曲线,复习时选题要突出这两个问题.

2.1要掌握求曲线方程的思路和方法.

求曲线方程的方法有多种,但其思路的实质都是根据曲线上点适合的共同条件找出动点的流动坐标和之间的关系式。常见的求曲线方程的类型有两种,一种是曲线形状明确且便于用标准形式表示,这时可用特定系数法求其方程;一种是曲线形状不明确或不便于用标准形式表示,这时一般地可用直接法,间接代点法,参数法等求方程。

2.2要强化解析几何的基本思想和方法

解析几何的基本思想是在平面直角坐标系中,把点与实数对,曲线与方程,区域与不等式统一起来,用代数方法研究平面上的几何问题.其中最重点的内容是用方程研究曲线,其次是用不等式研究区域问题.研究这一基本思想的实质是等价转化的思想。

2.3复习中要掌握常用的解题策略

平面解析几何是综合性较强的学科，因而解题时就需要运用多种知识、采用多种数学手段。熟记各种定义、基本公式、法则，做到迅速、准确解题。

3、注意解析几何与相关学科的交叉问题
　　由于解析几何内容在直线与圆锥曲线的几何性质和综合应用方面，涉及的内容丰富，易于纵横联系，对培养学生的数学素质，提高能力和继续学习有重要作用。这就启示我们在备考复习中，应高度重视解析几何与相关学科交叉知识问题的综合应用。04年高考题也给我们揭示了重视这一问题的重要性。应该说，解析几何中的圆锥曲线都是与方程理论相联系的，但在复习过程中，我们不应只停留在这一联系，而应尽可能加强解析几何和函数，解析几何与导数、平面向量的联系。在此，我们特别强调的是应有机加大解几和函数有关性质的联系。

　4、专题复习要立足课堂、讲究实效

　在实施专题复习的过程中，要对《考试大纲》所涉及的解析几何近30个知识点逐一排查，以题型为线索有针对性精心选题。小题选题要以课本为生长点，一方面要注意知识的覆盖面，同时也要注意知识的内部联系。解答题在选题时要以某圆锥曲线为背景，加强知识的纵横联系，如与函数、不等式、平面向量、导数的联系。用2~3个专题复习解析几何。小题1~2个课时，解答题1~2个课时。