08年高三数学第一学期期末考试试卷
说明:1、本卷满分150分,答卷时间100分钟.
2、答卷一律在答题纸上进行,只交答题纸.
一、选择题(单项选择题,12小题,每题5分)
1.下列函数中,最小正周期为![]() 的是 ( )
的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.命题:“若![]() ,则
,则![]() ”的逆否命题是( )
”的逆否命题是( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
3.已知等差数列![]() 的公差为2, 若
的公差为2, 若![]() 成等比数列, 则
成等比数列, 则![]() =( )
=( )
A . –4 B. –6 C. –8 D. –10
4.已知函数![]() 是
是![]() 的反函数,若
的反函数,若![]() 的图象过点(3,4),则
的图象过点(3,4),则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
5.设集合A={![]()
![]() 2<
2<![]() } ,B={
} ,B={![]()
![]() <2},若A∩B=A, 则实数
<2},若A∩B=A, 则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() <4
B.
<4
B. ![]() £4 C. 0<
£4 C. 0<![]() £4 D. 0<
£4 D. 0<![]() <4
<4
6.已知![]() =(2,3),
=(2,3),![]() =(-4,7),则
=(-4,7),则![]() 在
在![]() 方向上的投影为( )
方向上的投影为( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]()
D
D![]()
![]()
7.对于椭圆![]() ,
,![]() 是两焦点,若P为椭圆上一点,则
是两焦点,若P为椭圆上一点,则![]() .现已知P为椭圆
.现已知P为椭圆![]() 上的点,若
上的点,若![]() ,则
,则![]() 的面积是( )
的面积是( )
A.![]() B.
B.![]() C.
C.![]() D. 16
D. 16
8.在![]() 中,
中,![]() 是
是![]() 边上一点,若
边上一点,若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知![]() 为非零实数,且
为非零实数,且![]() ,则下列命题成立的是( )
,则下列命题成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设抛物线![]() 与过焦点的直线交于
与过焦点的直线交于![]() 两点,则
两点,则![]() 的值( )
的值( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
11.在棱长为2的正方体ABCD—A,B,C,D,中,O是底面ABCD的中心,E、F分别是CC,、AD的中点,那么异面直线OE和FD,所成的角的余弦值等于( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
12.定义行列式运算![]() =
=![]() .将函数
.将函数![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位,所得图象对应的函数为偶函数,则
)个单位,所得图象对应的函数为偶函数,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共4小题,每小题5分,共20分)
13.函数![]() 的定义域为 .
的定义域为 .
14.过长方体的同一个顶点的三条棱长为3、4、5,且它的八个顶点都在一个球面上,这个球的表面积是 .
15.若椭圆![]() 的离心率为
的离心率为![]() ,则双曲线
,则双曲线![]() 的离心率为_____.
的离心率为_____.
16.定义“符号函数”f(x)=sgnx=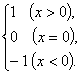 则不等式x+2>(x-2)sgnx的解集是_______.
则不等式x+2>(x-2)sgnx的解集是_______.
高三第一学期期末考试数学试卷答题纸
一 、选择题:(每小题5分)
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:(每小题5分)
13__________ 14_________ _
15_________ _ 16_________ _
三、解答题:
17. (本小题满分10分)在![]() 中,
中,![]() ,求
,求![]() 的值和
的值和![]() 的面积.
的面积.
18.(本题满分12分)已知函数![]()
![]() 的图象与
的图象与![]() 轴分别相交于点A、B两点,且
轴分别相交于点A、B两点,且![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() ,当
,当![]() 满足
满足![]() 时,求函数
时,求函数![]() 的最小值.
的最小值.
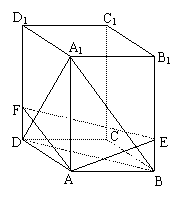
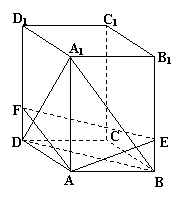 19. (本题满分12分)正四棱柱ABCD-A1B1C1D1的底面边长是
19. (本题满分12分)正四棱柱ABCD-A1B1C1D1的底面边长是![]() ,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
(Ⅰ)求证:A1C⊥面AEF;
(Ⅱ)求截面AEF与底面ABCD所成的二面角的大小;
20. (本题满分12分) 设数列{![]() }为等差数列,Sn为数列{
}为等差数列,Sn为数列{![]() }的前n项和,已知S7=7,S15=75,Tn为数列{
}的前n项和,已知S7=7,S15=75,Tn为数列{![]() }的前n项和,求Tn.
}的前n项和,求Tn.
21. (本题满分12分)已知函数![]() 是定义在
是定义在![]() 上的周期函数,周期
上的周期函数,周期![]() ,函数
,函数![]() 是奇函数
是奇函数![]() 又知
又知![]() 在
在![]() 上是一次函数,在
上是一次函数,在![]() 上是二次函数,且在
上是二次函数,且在![]() 时函数取得最小值
时函数取得最小值![]()
![]()
(Ⅰ)证明:![]() ;
;
(Ⅱ)求![]() 的解析式;
的解析式;
(Ⅲ)求![]() 在
在![]() 上的解析式
上的解析式![]()
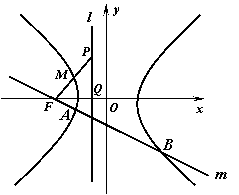
22. (本题满分12分)如图,点![]() 为双曲线
为双曲线![]() 的左焦点,左准线
的左焦点,左准线![]() 交
交![]() 轴于点
轴于点![]() ,点P是
,点P是![]() 上的一点,已知
上的一点,已知![]() ,且线段PF的中点
,且线段PF的中点![]() 在双曲线
在双曲线![]() 的左支上.
的左支上.
(Ⅰ)求双曲线![]() 的标准方程;
的标准方程;
 (Ⅱ)若过点
(Ⅱ)若过点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的左右两支分别交于
的左右两支分别交于![]() 、
、![]() 两点,设
两点,设![]() ,当
,当![]() 时,求直线
时,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
高三第一学期期末考试数学参考答案
一 、选择题:(每小题5分)
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | B | D | B | C | B | A | C | B | B | B |
二、 填空题:(每小题5分)
13.__________ ![]() 14.________ 50π
_
14.________ 50π
_
15._________ ![]() _ 16._________ (-
_ 16._________ (-![]() ,+∞) _
,+∞) _
三、解答题:
17. (本小题满分10分)解:![]()
![]() ,
,
所以![]() ,
,
![]()
18(本题满分12分)解: (1)由已知得A(![]() ,0), B(0,b), 则
,0), B(0,b), 则![]() =(
=(![]() ,b),于是
,b),于是![]() =2,b=2. ∴
=2,b=2. ∴![]() .
.
(2)由f(x)> g(x),得x+2>x2-x-6,即(x+2)(x-4)<0, 得-2<x<4,
![]() =
=![]() =x+2+
=x+2+![]() -5
-5
 由于x+2>0,则
由于x+2>0,则![]() ≥-3,当且仅当x+2=1,即x= -1时等号成立. ∴
≥-3,当且仅当x+2=1,即x= -1时等号成立. ∴![]() 的最小值是-3.
的最小值是-3.
19.(本题满分12分)解:(Ⅰ)证明:∵CB⊥面A1B,∴A1C在平面A1B
上的射影为A1B,又∵A1B⊥AE,∴A1C⊥AE,
同理A1C⊥AF, 又AE∩AF=A,∴A1C⊥面AEF;
方法2:以A为坐标原点,AB为x轴,AD为y轴,AA1为z轴建立直角坐标系,则B(![]() ,0,0),A(0,0,3),设E(
,0,0),A(0,0,3),设E(![]() ,0,yE)
,0,yE)
∵![]() ⊥
⊥![]() ,而
,而![]() =(-
=(-![]() ,0,3),
,0,3),![]() =(
=(![]() ,0,yE),∴
,0,yE),∴![]()
![]() =0,即
=0,即![]() ×
×![]() +0×0+3×yE =0,得yE
=1,
+0×0+3×yE =0,得yE
=1,
∴E(![]() ,0,1),而C(
,0,1),而C(![]() ,
,![]() ,0),
,0),
∴![]() =(
=(![]() ,
,![]() ,-3),∴
,-3),∴![]()
![]() =
=![]() ×
×![]() +
+![]() ×0+(-3)×1=0,
×0+(-3)×1=0,
∴![]() ⊥
⊥![]() ,
,
同理![]() ⊥
⊥![]() ,又AE∩AF=A,∴A1C⊥面AEF.
,又AE∩AF=A,∴A1C⊥面AEF.
(Ⅱ)A1B⊥AE,AA1⊥AB,∴∠BA1A=∠EAB.∴Rt△A1AB∽Rt△ABE,
∴![]() 又∵AB=
又∵AB=![]() ,A1A=3,∴EB=1,AE=
,A1A=3,∴EB=1,AE=![]() =2,
=2,
同理DF=1,AF=2,∵EF∥BD,∴EF∥面ABCD,
∴过A作直线l∥EF,则l为 面AEF与面ABCD的交线,
过B作BM⊥l于M,连EM,∵EB∥面ABCD,∴BM是EM在面ABCD内的射影,
∴EM⊥l, ∴∠EMB是所求的二面角的平面角,
BM=![]() ,tan∠EMB=
,tan∠EMB=![]() =
=![]() ,∴∠EMB=arctan
,∴∠EMB=arctan![]()
方法2:设截面AEF与底面ABCD所成的二面角为![]() ,
,
因为△ABD为AEF在底面ABCD上的射影三角形,则cos![]() =
=![]() ,
,
而S△ABD=![]() ,S△AEF=
,S△AEF=![]() ,所以cos
,所以cos![]() =
=![]() ,
,![]() =arccos
=arccos![]() ;
;
截面AEF与底面ABCD所成的二面角为![]() ,则cos
,则cos![]() =cos
=cos![]() =
=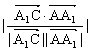
=![]() =
=![]() ,
,![]() =arccos
=arccos![]() .
.
方法3:![]() 面AEF的法向量,
面AEF的法向量,![]() 是面ABCD的法向量,
是面ABCD的法向量,![]() 与
与![]() 的夹角为
的夹角为![]()
20. (本题满分12分)法一:设{an}首项为a1,公差为d,则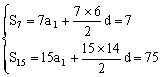
∴ ![]() ∴
∴ ![]() ∴
∴
![]()
此式为n的一次函数
∴ {![]() }为等差数列 ∴
}为等差数列 ∴ ![]()
法二:{an}为等差数列,设Sn=An2+Bn
∴ 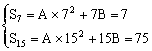
解之得: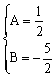
∴ ![]() ,下略
,下略
21.(本题满分12分)解:(Ⅰ)∵![]() 是以
是以![]() 为周期的周期函数,∴
为周期的周期函数,∴![]() ,
,
又∵![]() 是奇函数,∴
是奇函数,∴![]() ,
,
∴![]()
![]()
(Ⅱ)当![]() 时,由题意可设
时,由题意可设![]() ,
,
由![]() 得
得![]() ,∴
,∴![]() ,
,
∴![]()
![]()
(Ⅲ)∵![]() 是奇函数,∴
是奇函数,∴![]() ,
,
又知![]() 在
在![]() 上是一次函数,
上是一次函数,
∴可设![]() ,而
,而![]() ,
,
∴![]() ,∴当
,∴当![]() 时,
时,![]() ,
,
从而当![]() 时,
时,![]() ,故
,故![]() 时,
时,![]()
![]()
∴当![]() 时,有
时,有![]() ,∴
,∴![]()
![]()
当![]() 时,
时,![]() ,∴
,∴![]()
∴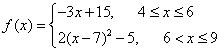
![]()
22.(本题满分12分)(Ⅰ)设双曲线方程为![]() (
(![]() ,
,![]() ),
),
则![]() …①,
…①,
![]() ,∴
,∴![]() …②.
…②.
又![]() 在双曲线上,∴
在双曲线上,∴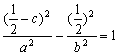 …③.(4分)
…③.(4分)
联立①②③,解得![]() ,
,![]() .∴双曲线方程为
.∴双曲线方程为![]() .(2分)
.(2分)
注:对点M用第二定义,得![]() ,可简化计算.
,可简化计算.
(Ⅱ)![]() ,设
,设![]() ,
,![]() ,m:
,m:![]() ,则
,则
由![]() ,得
,得![]() ,
,![]() .(2分)
.(2分)
由![]() ,得
,得![]() .
.
∴![]() ,
,![]() .
.![]() .(2分)
.(2分)
由![]() ,
,![]() ,
,![]() ,消去
,消去![]() ,
,![]() ,
,
得![]() .
.
∵![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,∴
,∴![]() .(2分)
.(2分)
又直线m与双曲线的两支相交,即方程![]() 两根同号,
两根同号,
∴![]() . ∴
. ∴![]() ,故
,故![]() .
.