高考数学总复习第九讲：怎样解填空题

高考数学总复习第九讲：怎样解填空题

考点梳理

一、题型特点

填空题和选择题同属客观性试题，它们有许多共同特点：其形态短小精悍，考查目标集中，答案简短、明确、具体，不必填写解答过程，评分客观、公正、准确等等。

不过填空题和选择题也有质的区别。首先，表现为填空题没有备选项。因此，解答时既有不受诱误的干扰之好处，又有缺乏提示的帮助之不足，对考生独立思考和求解，在能力要求上会高一些，长期以来，填空题的答对率一直低于选择题的答对率，也许这就是一个重要的原因。其次，填空题的结构，往往是在一个正确的命题或断言中，抽去其中的一些内容（既可以是条件，也可以是结论），留下空位，让考生独立填上，考查方法比较灵活。在对题目的阅读理解上，较之选择题，有时会显得较为费劲。当然并非常常如此，这将取决于命题者对试题的设计意图。

填空题与解答题比较，同属提供型的试题，但也有本质的区别。首先，解答题应答时，考生不仅要提供出最后的结论，还得写出或说出解答过程的主要步骤，提供合理、合法的说明。填空题则无此要求，只要填写结果，省略过程，而且所填结果应力求简练、概括和准确。其次，试题内涵，解答题比起填空题要丰富得多。填空题的考点少，目标集中，否则，试题的区分度差，其考试信度和效度都难以得到保证。这是因为：填空题要是考点多，解答过程长，影响结论的因素多，那么对于答错的考生便难以知道其出错的真正原因。有的可能是一窍不通，入手就错了，有的可能只是到了最后一步才出错，但他们在答卷上表现出来的情况一样，得相同的成绩，尽管它们的水平存在很大的差异。对于解答题，则不会出现这个情况，这是因为解答题成绩的评定不仅看最后的结论，还要看其推演和论证过程，分别情况评定分数，用以反映其差别，因而解答题命题的自由度，较之填空题大得多。由此可见，填空题这种题型介于选择题与解答题这两种题型之间，而且确定是一种独立的题型，有其固有的特点。

二、考查功能

1．填空题的考查功能大体上与选择题的考查功能相当

同选择题一样，要真正发挥好填空题的考查功能，同样要群体效应。但是，由于填空题的应答速度难以追上选择题的应答速度，因此在题量的使用上，难免又要受到制约。从这一点看，一组好的填空题虽然也能在较大的范围内考查基础知识、基本技能和基本思想方法，但在范围的大小和测试的准确性方面填空题的功能要弱于选择题。不过，在考查的深入程度方面，填空题要优于选择题。作为数学填空题，绝大多数是计算型（尤其是推理计算型）和概念（性质）判断型的试题，应答时必须按规则进行切实的计算或者合乎逻辑的推演和判断，几乎没有间接方法可言，更是无从猜答，懂就是懂，不懂就是不懂，难有虚假，因而考查的深刻性往往优于选择题。但与解答题相比其考查的深度还是差得多。就计算和推理来说，填空题始终都是控制在低层次上的。

2．填空题的另一个考查功能，就是有效地考查阅读能力、观察和分析能力。

在高考数学考试中，由于受到考试时间和试卷篇幅的限制，在权衡各种题型的利弊和考查功能的互补时，填空题由于其特点和功能的限制，往往被放在较轻的位置上，题量不多。

三、思想方法

同选择题一样，填空题也属小题，其解题的基本原则是“小题不能大做”。解题的基本策略是：巧做。解题的基本方法一般有：直接求解法，图像法和特殊化法（特殊值法，特殊函数法，特殊角法，特殊数列法，图形特殊位置法，特殊点法，特殊方程法，特殊模型法）等。

例题解析

一、直接求解法——直接从题设条件出发，利用定义、性质、定理、公式等，经过变形、推理、计算、判断得到结论的，称之为直接求解法。它是解填空题的常用的基本方法。使用直接法解填空题，要善于透过现象抓本质，自觉地、有意识地采取灵活、简捷的解法。

【例1】　已知数列{a_n}、{b_n}都是等差数列，a₁=0、b₁= -4，用S_k、S′_k、分别表示数列{a_n}、{b_n}的前k项和（k是正整数），若S_k+S′_k =0，则a_k+b_k的值为　　　　　　　　　　　　　　　　　　　　 。

【解】　法一　 直接应用等差数列求和公式S_k=，得+=0，又a₁+b₁= -4, ∴a_k+b_k=4。

法二　由题意可取k=2（注意：k≠1，为什么？），于是有a₁+a₂+b₁+b₂=0，因而a₂+b₂=4,即a_k+b_k=4。

【例2】　乒乓球队的10名队员中有3名主力队员，派5名参加比赛。3名主力队员要安排在第一、三、五位置，其余7名队员选2名安排在第二、四位置，那么不同的出场安排共有　　　　　　　　 种（用数字作答）。

【解】　三名主力队员的排法有P₃³种，其余7名队员选2名安排在第二、四位置上有P₇²种排法，故共有排法数A₃³A₇²=252种。

【例3】　如图14-1，E、F分别为正方体的面ADD₁A₁、面BCC₁B₁的中心，则四边形BFD₁E在该正方体的面上的射影可能是　　　　　　　　　　　　 （要求：把可能的图的序号都填上）。

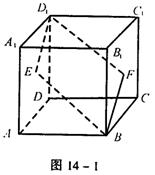
【解】　正方体共有3 组对面，分别考察如下：（1）四边形BFD₁E在左右一组面上的射影是图③。因为B点、F点在面AD₁上的射影分别是A点、E点。（2）四边形BFD₁E在上下及前后两组面上的射影是图②。因为D₁点、E点、F点在面AC上的射影分别是D点、AD中点、BC中点；B点、E点、F点在面DC₁上的射影分别是C点、DD₁的中点、CC₁的中点。故本题答案为②③。

【例4】　已知抛物线的焦点坐标为F(2,1)，准线方程为2x+y=0，则其顶点坐标为　　　　　　　　　　　　　　　　　　　　　　 　　　　　　。

【解】　过焦点F(2,1)作准线的垂线段，由解几何知识可得抛物线顶点为垂线段的中点。又由于准线的斜率k= -2,k_OF=，∴O为垂足，从而易得OF的中点，即顶点为(1, )。

【例5】　老师给出一个函数y=f(x)，四个学生甲、乙、丙、丁各指出这个函数的一个性质：

甲：对于x∈R，都有f(1+x)=f(1-x)　　　　　　　　　　　　　　　　　乙：在 (-∞,0上函数递减

丙：在(0,+∞)上函数递增　　　　　　　　　　　　　　　　　　　　　　　　丁：f(0)不是函数的最小值

如果其中恰有三人说得正确，请写出一个这样的函数　　　　　　　　　 。

【解】　由题意知，以甲、乙、丙、丁四个条件中任意三个为一组条件，写出符合条件的一个函数最可。例如同时具备条件甲、乙、丁的一个函数为y=(x-1)²。

【例6】　若-=1，则sin2θ的值等于　　　　　　　　　　　　　　　　　　 。

【解】　由-=1得sinθ-cosθ=sinθcosθ　 ①

令sin2θ=t，则①式两边平方整理得t²+4t-4=0，解之得t=2-2。

【例7】　已知z₁=3+4i,z₂= -2-5i,则arg()=　　　　　　　　　　　　　　　　　　。

【解】　将z₁=3+4i,z₂= -2-5i代入整理得=3i，故arg()=。

【例8】　若(+)ⁿ展开式中的第5项为常数，则n=　　　　　　　　　　　　　。

【解】　由T_r+1=C_n^r()^n-r()^r=C_n^r2^rx及题意可知，当r=4时，n-3r=0，∴n=12。

二、图像法——借助图形的直观形，通过数形结合的方法，迅速作出判断的方法称为图像法。文氏图、三角函数线、函数的图像及方程的曲线等，都是常用的图形。

【例9】　若关于x的方程=k(x-2)有两个不等实根，则实数k的取值范围是　　　　　　　　　　　　　　　　　　　　　 。

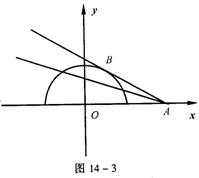
【解】　令y₁=,y₂=k(x-2),由图14-3可知k_AB<k≤0，其中AB为半圆的切线，计算k_AB= -,∴-<k≤0。

【例10】　已知两点M(0,1),N(10,1) ，给出下列直线方程

①5x-3y-22=0;②5x-3y-52=0;③x-y-4=0;④4x-y-14=0。在直线上存在点P满足MP=NP+6的所有直线方程的序号是　　　　　　　　　　　　　 。

【解】　由MP=NP+6可知，点P的轨迹是以M（0，1），N（10，1）为焦点，实轴长为6的双曲线的右支，其方程为-=1，(x≥5)。本题实质上可转化为考察所给直线与双曲线的右支有无交点问题，结合图形判断，易得（2）（3）直线与双曲线的右支有交点。

【例11】　点P(x,y)是曲线C：(θ为参数，0≤θ<π)上任意一点，则的取值范围是　　　　　　 　　　　　　　　　　　　。

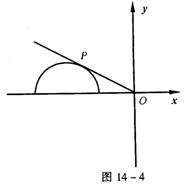
【解】　曲线C的普通方程为(x+2) ² +y²=1(y≥0)，则可视为P点与原点O连线的斜率，结合图形（14-4）判断易得的取值范围是[-，0]。

三、特殊化法——当填空题的结论唯一或其值为定值时，我们只须把题中的参变量用特殊值（或特殊函数、特殊角、特殊数列、图形特殊位置、特殊点、特殊方程、特殊模型等）代替之，即可得到结论。

1.特殊值法

【例12】　设a>b>1，则log_ab,log_ba,log_abb的大小关系是　　　　　　　　　　　　　　　　　　　 。

【解】　考虑到三个数的大小关系是确定的，不妨令a=4,b=2，则log_ab=,log_ba=2,log_abb=,

∴log_abb<log_ab<log_ba

2．特殊函数法

【例13】　如果函数f(x)=x²+bx+c对任意实数t都有f(2+t)=f(2-t)，那么f(1),f(2),f(4)的大小关系是　　　　　　　　　　 　　　　　　　　　　　　。

【解】　由于f(2+t)=f(2-t)，故知f(x)的对称轴是x=2。可取特殊函数f(x)=(x-2)²,即可求得f(1)=1,f(2)=0,f(4)=4。∴f(2)<f(1)<f(4)。

3．特殊角法

【例14】　cos²α+cos²(α+120°)+cos²(α+240°)的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 。

【解】　本题的隐含条件是式子的值为定值，即与α无关，故可令α=0°，计算得上式值为。

【例15】　已知等差数列{a_n}的公差d≠0，且a₁,a₃,a₉成等比数列，则的值是　　　　　　　　　　　　　　　 。

【解】　考虑到a₁,a₃,a₉的下标成等比数列，故可令a_n=n满足题设条件，于是=。

5．图形特殊位置法

【例16】　已知SA，SB，SC两两所成角均为60°，则平面SAB与平面SAC所成的二面角　　　　　　　　　　　　　　　 　　　　　　。

【解】　取SA₁=SB₁=SC₁，将问题置于正四面体中研究，不难得平面SAB与平面SAC所成的二面角为arccos。

6．特殊点法

【例7】　椭圆+=1的焦点为F₁、F₂，点P为其上的动点，当∠F₁PF₂为钝角时，点P横坐标的取值范围是　　　　　　　　　　　　　　　　　　　　　　　 。

【解】　设P(x,y)，则当∠F₁PF₂=90°时，点P的轨迹方程为x²+y²=5，由此可得点P的横坐标x=±，又当点P在x轴上时，∠F₁PF₂=0；点P在y轴上时，∠F₁PF₂为钝角，由此可得点P横坐标的取值范围是-<x<。

7．特殊方程法

【例18】　直线l过抛物线y²=a(x+1)(a>0)的焦点，并且与x轴垂直，若l被抛物线截得的线段长为4，则a=　　　　　　　　　　　　　　　　　　　　 。

【解】　∵抛物线y²=a(x+1)与抛物线y²=ax具有相同的垂直于对称轴的焦点弦长，故可用标准方程y²=ax替换一般方程y²=a(x+1)求解，而a值不变。由通径长公式得a=4。

8．特殊模型法

【例19】　已知m,n是直线，α、β、γ是平面，给出下列是命题：

①若α⊥γ，β⊥γ，则α∥β；

②若n⊥α，n⊥β，则α∥β；

③若α内不共线的三点到β的距离都相等，则α∥β；

④若nα，mα且n∥β,m∥β，则α∥β；

⑤若m,n为异面直线，n∈α，n∥β，m∈β,m∥α,则α∥β；

则其中正确的命题是　　　　　　　　　　　　　　　　　　　　　　。（把你认为正确的命题序号都填上）。

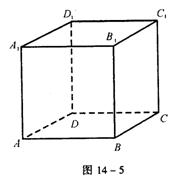
【解】　依题意可构造正方体AC₁，如图14-5，在正方体中逐一判断各命题易得正确命题的是②⑤。

　　　　　

 

四、构造法——在解题时有时需要根据题目的具体情况，来设计新的模式解题，这种设计工作，通常称之为构造模式解法，简称构造法。

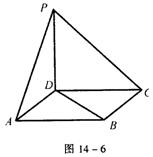
【例20】　如图14-6，点P在正方形ABCD所在的平面外，PD⊥ABCD，PD=AD，则PA与BD所成角的度数为 　　　　　　　　　　　　　　　　　 。

【解】　根据题意可将右图补形成一正方体，在正方体中易求得60°。

	本周强化练习：

跟踪练习

1．设等差数列{a_n}共有3n项，它的前2n项之和是100，后2n项之和是200，则该等差数列的中间n项之和等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 。

2．设{a_n}是首项为1的正项数列，且(n+1)a_n+1²-na_n²+a_n+1a_n=0(n=1,2,3，…)，则它的通项公式是a_n=　　　　　　　　　　　　　　　　。

3．从7盆不同的盆花中选出5盆摆放在主席台前，其中有两盆花不宜摆放在正中间，则一共有　　　　　　　　　　　　 　　　　　　种不同的摆放方法（用数字作答）

4．将正方形ABCD沿对角线AC折成直二面角后，异面直线AB与CD所成角的大小是　　　　　　　　　　　　　　　　　　　　　　　　　。

5．抛物线x²-8x-4y+c=0 焦点在x轴上，则常数c=　　　　　　　　　　　　　　　　　。

6．将1，2，3，4，5，6，7，8，9，这九个数排成三横三纵的方阵，要求每一列的三个数从前到后都是由小到大排列，则不同的排法种数是　　　　　　　　　　　　　　　　　　　　　　（用数字作答）。

7．已知三棱锥的一条棱长为1，其余各棱长皆为2，则此三棱锥的体积为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　。

8．已知三个不等式：

①ab>0,②-<-,③bc>ad

以其中两个作为条件，余下一个作为结论，则可以组成　　　　　　　　　　　　　　　　　　　个正确的命题。

9．设函数f(x)的反函数为h(x)，函数g(x)的反函数为h(x+1)，已知f(2)=5,f(5)= -2,f(-2)=8，那么g(2),g(5),g(8),g(-2)中，一定能求出具体数值的是　　　　　　　　　　　　 。

10．A点是圆C：x²+y²+ax+4y-5=0上任意一点，A点关于直线x+2y-1=0的对称点也在圆C上，则实数a=　　　　 　　　　　　　　　　　　。

11．已知向量a与向量b的夹角为60°，且a=3,b=2,c=3a+5b,d=ma-3b，若c与d垂直，则m的值为　　　　　　　 　　　　　　　　　　　　。

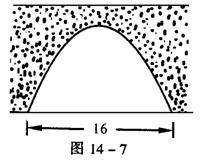
12．某桥的桥洞呈抛物线形（如图14-7）桥下水面宽16米，当水面上涨2米后达到警戒水位，水面宽变为12米，此时桥洞顶部距水面高度为　　　　　　　　　　　　　　　　米。（精确到0.1米）

13．以椭圆+=1的中心O为顶点，以椭圆的左准线l₁为准线的抛物线与椭圆的右准线l₂交于A、B两点，则AB的值为　　　　　　　　　　　　　　　　　　　　　 。

14．已知sinαcosα=,α∈(,)，则cosα-sinα的值为　　　　　　　　　　　　　　　　　　 。

15．已知椭圆+=1与双曲线-=1(m,n,p,q∈{xx是正实数集})，有共同的焦点F₁、F₂，P是椭圆和双曲线的一个交点，则PF₁·PF₂=　　　　　　　　　　　　　　　　　　　 。

16．函数y=sinxcosx+cos²x-的最小正周期是　　　　　　　　　　　　　　　　　　　　　 。

17．参数方程(θ是参数)所表示的曲线的焦点坐标是　　 　　　　　　　　　　　　　　　　　 。

18．(1+x)⁶(1-x)⁴展开式中x³的系数是　　　　　　　　　　　　　　　　　　　　 。

19．已知tanα=2,tan(α-β)= -，那么tanβ=　　　　　　　　　　　　　　　　　　　 。

20．不等式3<（）^x-2的解集为　　　　　　　　　　　　　　　　 　　　　　　。

21．一个球自12米高的地方自由下落，触地面后的回弹高度是下落高度的，到停止在地面上为止，则球运动的路程总和是　　　　　　　　　　　　　　　　 米。

22．已知a、b、c、d是四条互不重合的直线，且c、d分别为a、b在平面α上的射影，给出下面两组四个论断：

第一组：①a⊥b,②a∥b;

第二组：③c⊥d,④c∥d。

分别从两组中各选一个论断，使一个作条件，另一个作结论，写出一个正确的命题：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　。

23．函数y=f(x)的图像与y=2^x的图像关于直线y=x对称，则函数y=f(4x-x²)的递增区间是　　　　　　　　　　　　　　　　　　　　　　　。

24．已知α=arcsin(-)，则sin的值是　　　　　　　　　　　　　　　　　　 。

25．过抛物线y²=4x的焦点，且倾斜角为的直线交抛物线于P、Q两点，O是坐标原点，则△OPQ的面积等于　　　　　　　　　　　　　　　　　　　　　　　 。

26．一个三棱锥的三个侧面中有两个是等腰直角三角形，另一个是边长为1的正三角形，这样的三棱锥体积为　　　　　　　　　　　　　　　　　　 （写出一个可能值）。

27．从5名礼仪小姐、4名翻译中任选5名参加一次经贸洽谈活动，其中礼仪小姐、翻译均不少于2人的概率是　　　　　　　　　　　　　　　　　　　　　　　 。

28．定义在（-∞，+∞）上的偶函数f(x)满足：f(x+1)= -f(x)，且在[-1，0]上是增函数，下面是关于f(x)的判断：

①f(x)是周期函数；

②f(x)的图像关于直线x=1对称；

③f(x)在[0，1]上是增函数；

④f(x)在[1，2]上是减函数；

⑤f(2)=f(0)。

其中正确的判断是　　　　　　　　　　（把你认为正确的判断都填上）。

29．求值：=　　　　　　　　　　　　　　　　　　　　　　　　 。

30．复数z₁=2+i, z₂=1-i,复数z=，则z=　　　　　　　　　　　　　　　　　　　　　 。

31．已知正四棱柱的体积为定值V，则它的表面积的最小值为　　　　　　　　　　　　　　　　　　　　。

32．已知下列曲线：

以及编号为①②③④的四个方程 ：

①-=0　　　　　　　　　 ②x-y=0　　　　 ③x-y=0　　　　　 ④x-y=0

请按曲线ABCD的顺序，依次写出与之相对应的方程的编号：　　　　　　　　　　　　。

33．已知A、B、C、D为同一球面上的四点，且连接每两点间的线段长都等于2，则球心O到平面BCD的距离等于　　　　　　　　　　。

34．过点M（0，4）、被圆(x-1) ² +y²=4截得的线段为2的直线方程为　　　　　　　　　　　　　　　　 。

35．数列{a_n}满足a₁=,a₁+a₂+…+a_n=n²·a_n，则数列{a_n}的通项公式a_n=　　　　　　　　　　　　。

36．设函数f(x)=sin(ωx+)(ω>0, -<<)

给出以下四个论断：

①它的图像关于直线x=对称；

②它的图像关于点(,0)对称；

③它的周期是π；

④在区间[-，0]上是增函数。

以其中两个论断作为条件，余下论断作为结论，写出你认为正确的两个命题：

（1）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　；

（2）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　；

37．抛物线x=2(y-1)²-5的准线方程是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 。

38．设F₁，F₁是椭圆+=1的两个焦点，P是椭圆上一点，且PF₁-PF₂=1，则tan∠F₁PF₂=　　　　　　　　　　　　　　　　　　　　　　　.

39．已知tan(α+β)=,tan(β-)=，则tan(α+)的值是　　　　　　　　　　　　　　 。

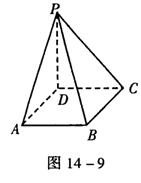
40．如图14-9，四棱锥P—ABCD的底面ABCD是一个正方形，PD垂直于底面ABC则这个四棱锥的五个面中，互相垂直的平面共有　　　　　　  对。

　　　　

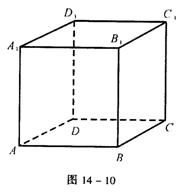
41．如图14-10，已知正方体ABCD—A₁B₁C₁D₁，过点A作截面，使正方体的12条棱所在直线与截面所成的角皆相等，试写出满足这样条件的一个截面　　　　　　　　  。

（注：只需任意写出一个）

42．直线l经过抛物线y²=4x的焦点，且与准线成60°角，则直线l的方程是　　　　　　　　　　　　　　 。

（注：填上你认为正确的一个方程即可，不必考虑所有可能的情况）

43．若tanα=，则cos2α+3sin²α=　　　　　　　　　　　　　　　。

44．在平面α内有一个正三角形ABC，以BC边为轴把△ABC旋转θ角θ∈（0，），得到△A′BC，当θ=　　　　　　　　　　　　　时，△A′BC在平面α的射影是直角三角形。

45．求值：tan[arcsin(-)]=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　。

46．圆心在抛物线y²=8x上，与抛物线的准线相切且过坐标原点的圆的方程为　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　。

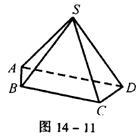
47．如图14-11，四棱锥S—ABCD的四条侧棱相等，且底面是梯形，AD∥BC，AD>BC，当梯形ABCD满足条件　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　时，点S在底面ABCD上射影O位于梯 ABCD外边。（注：只需填上你认为正确的一个条件即可，不必考虑所有可能情况）

48．给出下面4个命题：

①y=tanx在第Ⅰ象限是增函数；

②奇函数的图像一定过原点；

③f^-1(x)是f(x)的反函数，如果它们的图像有交点，则交点必在直线y=x上；

④“a>b>1”是“log_ab<2”的充分但不必要条件。

其中正确的命题的序号是　　　　　　　（把你认为正确的命题的序号都填上）。

49．函数y=(x≤-1)的反函数是　　　　　　　　　　　。

参考答案

1.75　2. 　3.1800　4. 　5.12　6.1680　7. 　8.3　9.g(2),g(5),g(-2　)10.-10　11.2　12.2.6　13. 　14. 　15.m-p　16. π　17.(3,- )　18.-8　19.12　20.{x-2<x<1}　21.20　22.a∥bc∥d　23.(0,2　24. -　25.2　26. 、、　27. 　28.①②⑤　29.- 　30. 　31.6　32. ④②①③　33. 　34.x=0或15x+8y-32=0　35.　36.(1) ①③②④　(2) ②③①④　37.X= -　38. 　39. 　40.5对　 41.截面AB₁D₁，或截面ACD₁，或截面AB₁C　42. x-3y-=0（或）x+3y-=0　43. 　44.arccos　45.- 　46.(x-1)²+(y±2)²=9  47. ∠ABD>90°（或∠ACD>90°）或∠BAD+∠ADB<90°，或∠ADC+∠CAD<90°)　48. ③④　49.y=-(x≥0)