高考复习试题之十一排列

高三单元试题之十一排列、组合和二项式定理

(时量：120分钟 满分：150分)

一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1．设则(a₀+a₂+a₄)²－(a₁+a₃)²的值为(　　)　　　　　　　　　　　　　　 

　　　 A．1　　　　　　　　　　　　B．－1　　　　　　　　　　 C．0　　　　　　　　　　　　D．2

2．从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作，其中甲、乙两名志愿者不能从事翻译工作，则不同的选排方法共有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．96种　　　　　　　　　B．180种　　　　　　　　 C．240种　　　　　　　　D．280种

3．五种不同的商品在货架上排成一排，其中a 、b两种必须排在一起，而c、d两种不能排在一起，则不同的排法共有　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．12种　　　　　　　　　B．20种　　　　　　　　　C．24种　　　　　　　　　D．48种

4．某团支部进行换届选举，从甲、乙、丙、丁四人中选出三人分别担任书记、副书记、组织委员。规定上届任职的甲、乙、丙三人不能连任原职，则不同的任职方案有　　 （ 　 ）

　　　 A．10　　　　　　　　　　　B．11　　　　　　　　　　　 C．12　　　　　　　　　　　D．13

5．直线方程Ax+By=0，若从0，1，2，3，5，7这六个数字中每次取两个不同的数作为系数A、B的值，则方程表示不同直线的条数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　 　A．2　　　　　　　　　　 　B．12　　　　　　　　　　　 C．22　　　　　　　　　 　D．25

6．六个人排成一排，甲乙两人中间至少有一个人的排法种数有　　　　　　　　　　　　　　　（　　）

　　　 A．480　　　　　　　　　　 B．720　　　　　　　　　　 C．240　　　　　　　　　　 D．360

7．a∈{1，2，3}，b∈{3，4，5，6，7，8}，r∈{1，2，3}，则方程(x－a)²+(y－b)²＝r²所表示的圆共有 　　　　　　　　　　　　　　　　　（　　）

A．12个　　　　　　　　　B．18个 　　　　　　　　 C．36个　　　　　　　　　D． 54个

8．若(1－2x)⁵的展开式中第二项小于第一项，且不小于第三项，则x的取值范围是（　　）

　　　A．x>－　　　　　　　B．x≥－　　　　　　 C．－≤x≤0　　　　D．－≤x≤0

9．从4名男生和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法共有　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　  (　　 )

A．34种　　　　　　　　B．35种　　　　　　C．120种　　  　　D．140种

10．将4名教师分配到3所中学任教，每所中学至少1名，则不同的分配方案共有（　 ）

A．12种　　 　　　　　　 　B．24种　　 　　　　　C．36种　　  　　D．48种

11．设的展开式中的各项系数之和为P，而它的二项式系数之和为S。若P+S=272，那么展开式中项的系数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．81　　　　　　　　　　　B．54　　　　　　　　　　　 C．—12　　　　　　　　　 D．1

12．从长度分别为1，2，3，4，5的五条线段中，任取三条的不同取法共有n种。在这些取法中，以取出的三条线段为边可组成的钝角三角形的个数为m，则等于　　（　　）

　　A．　　 　　　　　B．　　 　　　　　　　C．　　 　　　　　D．

二、填空题：本大题共4小题，每小题4分，共16分．答案填在题中横线上．

13．多项式(1－2x)⁶(1+x)⁴展开式中，x最高次项为　　　，x³系数为____。

14．的值为_______　　　　　  ．

15．七个人排成两排，前排3个，后排4个，若甲必须在前排，乙必须在后排，有____种不同排法.　

16．关于二项式(x－1)²⁰⁰⁵有下列命题：

　　　①该二项展开式中非常数项的系数和是1；

　　　②该二项展开式中第六项为x¹⁹⁹⁹；

　　　③该二项展开式中系数最大的项是第1002项；

　　　④当x=2006时，(x－1)²⁰⁰⁵除以2006的余数是2005。

　　　 其中正确命题的序号是　　　　  。（注：把你认为正确的命题序号都填上）

三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．

17．（本小题满分12分）某学习小组有8个同学，从男生中选2人，女生中选1人参加数学、物理、化学三种竞赛，要求每科均有1人参加，共有180种不同的选法，那么该小组中男、女同学各有多少人？

18．（本小题满分12分）某人手中有5张扑克牌，其中2张为不同花色的2，3张为不同花色的A，他有5次出牌机会，每次只能出一种点数的牌，但张数不限，此人有多少种不同的出牌方法？

 

19．（本小题满分12分）二项式的展开式中：

⑴求常数项；

⑵有几个有理项；

⑶有几个整式项。

　　　　　　　　　　　　　　 

20．（本小题满分12分）规定,其中x∈R，m为正整数，且＝1，这是排列数(n，m是正整数，且m≤n)的一种推广．

⑴求的值；

⑵排列数的两个性质：①＝n，　 ②+m＝．(其中m,n是正整数)是否都能推广到(x∈R，m是正整数）的情形？若能推广，写出推广的形式并给予证明；若不能，则说明理由；

⑶确定函数的单调区间．

21．(本小题满分12分)当n∈N且n>1时，求证2<(1+)ⁿ<3。

22．（本小题满分14分）一个同心圆形花坛，分为两部分，中间小圆部分种植草坪和绿色灌木，周围的圆环分为n(n≥3，n∈N)等份，种植红、黄、蓝三色不同的花，要求相邻两部分种植不同颜色的花.

⑴如图1，圆环分成的3等份为a₁，a₂，a₃，有多少不同的种植方法？如图2，圆环分成的4等份为a₁，a₂，a₃，a₄，有多少不同的种植方法？

⑵如图3，圆环分成的n等份为a₁，a₂，a₃，……，a_n，有多少不同的种植方法？

高三单元试题之十一排列、组合和二项式定理参考答案

一、1．A  2．C 3．C　4．B　5．C　6．A　7．D　8．D　9．A　10．C　11．D　12．B

二、13．64x¹⁰，12　 14．3¹⁰　 15．1440　　16．①④

三、17．解：设男生有x人，则女生有8－x人，依题意，＝180，

∴(8－x)·6=180，x³－9x²+8x+60=0，x³－5x²－(4x²－20x)－(12x－60)＝0，

(x－5)(x²－4x－12)＝0，∴x₁＝5，x₂＝6，x₃＝－2(舍)。

∴男生5人，女生3人；或男生6人，女生2人。

18．解：由于张数不限，2张2,3张A可以一起出，亦可分几次出，故考虑按此分类。

出牌的方法可分为以下几类：

⑴5张牌全部分开出，有种方法；

⑵2张2一起出，3张A一起出，有种方法；

⑶2张2一起出，3张A分开出，有种方法；

⑷2张2一起出，3张A分两次出，有种方法；

⑸2张2分开出，3张A一起出，有种方法；

⑹2张2分开出，3张A分两次出，有种方法；

因此共有不同的出牌方法＋＋＋＋＋＝860种.

19．展开式的通项为：T_r+1＝(－1)^r＝(－1)^r2^r，

⑴设T_r+1项为常数项，则＝0，得r=6，即常数项为T₇＝2⁶；

⑵设T_r+1项为有理项，则＝5－r为整数，∴r为6的倍数，

又∵0≤r≤15，∴r可取0，6，12三个数。

⑶5－r为非负整数，得r＝0或6，∴有两个整式项。

20．解：⑴；

⑵性质①、②均可推广，推广的形式分别是：

①，　　　　 ②

事实上，在①中，当时,左边，右边，等式成立；

当时，左边

，

  因此,①成立；

在②中，当时,左边右边，等式成立；

当时，左边

右边，

因此　②成立。

⑶先求导数，得.令>0,解得x<或 x>.

因此，当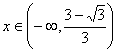时,函数为增函数,当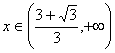时,函数也为增函数。

令<0,解得<x<.

因此,当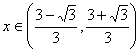时,函数为减函数.

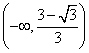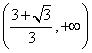∴函数的增区间为， ；减区间为。

21．证明：(1+)ⁿ＝1+++…+>1＋＝2。

(1+)ⁿ＝2+++…+

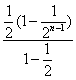<2+++…+<2+++…+＝2＋＝3－<3。

因此2<(1+)ⁿ<3(n>1且n∈N)。

22．解：⑴如图1，先对a₁部分种植，有3种不同的种法，再对a₂、a₃种植，

因为a₂、a₃与a₁不同颜色，a₂、a₃也不同。 所以S（3）=3×2=6（种）。

如图2，S（4）=3×2×2×2－S（3）=18（种）。

⑵如图3，圆环分为n等份，对a₁有3种不同的种法，对a₂、a₃、…、a_n都有两种不同的种法，但这样的种法只能保证a₁与a_i（i=2、3、……、n－1）不同颜色，但不能保证a₁与a_n不同颜色.

于是一类是a_n与a₁不同色的种法，这是符合要求的种法，记为种. 另一类是a_n与a₁同色的种法，这时可以把a_n与a₁看成一部分，这样的种法相当于对n－1部分符合要求的种法，记为.

共有3×2^n－1种种法.

这样就有.即，

则数列是首项为公比为－1的等比数列.

则

由⑴知：，∴.

∴.

答：符合要求的不同种法有