高三单元试题之五平面向量
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有
一项是符合题目要求的。）
1．已知△ABC的三个顶点A、B、C及所在平面内一点P满足
，则点P与△ABC的关系为是 （ ）
A．P在△ABC内部 B． P在△ABC外部
C．P在AB边所在直线上 D． P在△ABC的AC边的一个三等分点上
2．已知向量
，且P2点分有向线段
所成的比为－2，则
的坐标是 （ ）
A．(
B．(
) C．（7，－9） D．（9，－7）
3．设
分别是
轴，
轴正方向上的单位向量，
，
。若用a来表示
与
的夹角，则a等于 （ ）
A．
B．
C．
D．
4．若向量a=(cosa,sina)，b=(cosb,sinb)，则a与b一定满足 （ ）
A．a与b的夹角等于a－b B．(a＋b)⊥(a－b)
C．a∥b D．a⊥b
5．设平面上有四个互异的点A、B、C、D，已知（
则△ABC的形状是 （ ）
A．直角三角形 B．等腰三角形 C．等腰直角三角形D．等边三角形
6．设非零向量a与b的方向相反，那么下面给出的命题中，正确的个数是 （ ）
（１）a＋b＝0 （２）a－b的方向与a的方向一致
（３）a＋b的方向与a的方向一致 （４）若a＋b的方向与b一致，则a<b
A．１个 B．２个 C．３个 D．４个
7．已知p=
，q=3，p、q的夹角为45°，则以a=5p+2q，b=p－3q为邻边的平行四边形过a、b起点的对角线长为 （ ）
A．14 B．
C．15 D．16
8．下列命题中：
①
∥
存在唯一的实数
，使得
；
②
为单位向量，且∥，则=±·；③
；
④与共线，与
共线，则与共线；⑤若
其中正确命题的序号是 （ ）
A．①⑤ B．②③④ C．②③ D．①④⑤
9．在△ABC中，已知
的值为 （ ）
A．－2 B．2 C．±4 D．±2
10．已知，A（2，3），B（－4，5），则与
共线的单位向量是 （ ）
A．
B．
C．
D．
11．设点P分有向线段
所成的比为
，则点P1分
所成的比为 （ ）
A．
B．
C．
D．
12．已知
垂直时k值为 （ ）
A．17 B．18 C．19 D．20
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上．）
13．已知向量
的夹角为
，
．
14．把一个函数图像按向量
平移后，得到的图象的表达式为
，
则原函数的解析式为 ．
15．在△ABC中，A，B，C成等差数列，则
．
16．已知点A(2，0)，B(4，0)，动点P在抛物线y2＝－4x运动，则使
取得最小值的点P的坐标是
．
三、解答题（本大题共6小题，共74分．解答应有证明过程或演算步骤）
17．（本题12分）已知△ABC中,∠C＝120°，c=7,a+b=8,求
的值。
18．（本题12分）设向量
，向量
垂直于向量
，向量
平行于
，试求
的坐标．
19．（本题12分）已知M＝(1+cos2x，1)，N＝(1，
sin2x+a)(x，a∈R，a是常数)，且y=
·
(O是坐标原点)⑴求y关于x的函数关系式y=f(x)；
⑵若x∈[0，
]，f(x)的最大值为4，求a的值，并说明此时f(x)的图象可由y=2sin(x+
)的图象经过怎样的变换而得到．
20．（本题12分）已知A（－1，0），B（1，0）两点，C点在直线
上，且
，
成等差数列，记θ为
的夹角，求tanθ．
21．（本题12分）已知： 、、是同一平面内的三个向量，其中 ＝（1，2）
⑴若
，且
，求的坐标；
⑵若=
且
与
垂直，求与的夹角θ.
22．（本题14分）已知向量
⑴
;
⑵（理科做）若
（文科做）求函数
的最小值。
高三单元试题之五：平面向量参考答案
一、1．D 2．C 3．D 4．B 5．B 6．A 7．C 8．C 9．D 10．B 11．C 12．C
二、13．
14．
15． 16．(0，0)
三、17．解：解法1：由正弦定理：
，
代入
∴
解法2：由
∵
，∴
∴
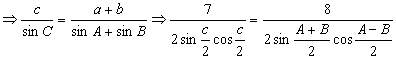
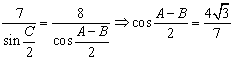
（也可由余弦定理求解）
18．解：设
，∴
，∴
①
又
即：
②
联立①、②得
∴ 
．
19．解：⑴y=·＝1+cos2x+sin2x+a，得f(x)
=1+cos2x+sin2x+a；
⑵f(x) =1+cos2x+sin2x+a化简得f(x)
=2sin(2x+)+a+1，x∈[0，]。
当x＝时，f(x)取最大值a＋3＝4，解得a＝1，f(x)
=2sin(2x+)+2。
将y=2sin(x+)的图象的每一点的横坐标缩短到原来的一半，纵坐标保持不变，再向上平移2个单位长度可得f(x)
=2sin(2x+)+2的图象。
20．解：设
又∵三者
，成等差数列．
当
，
同理
21．解：⑴设
由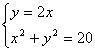
∴
或 
∴
⑵
……（※）
代入（※）中,
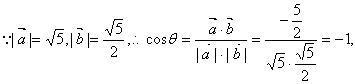
22．解：⑴
⑵（理科）
①当
时，当县仅当
时，
取得最小值－1，这与已知矛盾；
②当
时，取得最小值
，由已知得
；
③当
时，取得最小值
，由已知得
解得
，这与
相矛盾，综上所述，
为所求.
（2）（文科）
∴当且仅当
取得最小值
。