06届高三数学第一轮模拟试卷一
（立几、解几、概率等）
命题人：江阴市成化高级中学 张龙伍
一、选择题：本大题共10小题，每小题5分，共50分。
1、编号为1、2、3、4、5的五个人分别去坐编号为1、2、3、4、5的五个座位，其中有且只有两个人的编号与座位号一致的坐法有( )
A．10种 B．20种 C．30种 D．60种
2、正三棱锥的侧面都是直角三角形，侧棱与底面所成的角为
，则等于( )
A．
B．
C．
D．
3、设有如下三个命题：甲：相交直线
、m都在平面α内，并且都不在平面β内；乙：直线、m中至少有一条与平面β相交；丙：平面α与平面β相交．当甲成立时，( )
A．乙是丙的充分而不必要条件 B．乙是丙的必要而不充分条件
C．乙是丙的充分且必要条件 D．乙既不是丙的充分条件又不是丙的必要条件
4、将一个各个面上均涂有颜色的正方体，锯成64个同样大小的小正方体，从这些小正方体中任取一个，其中恰好有2面涂有颜色的概率是 （ ）
A、
B、
C、
D、
5、等体积的球和正方体，它们的表面积的大小关系是（ ）
A．
B．
C．
D．
6、地球半径为R，则南纬60°纬线圈的长为 （ ）
A．
B．
C．
D．R
7、一个容量为20的样本数据，分组后，组距与频数如下：
| 组距 | (10 , 20) | (20 , 30] | (30 , 40] | (40 , 50] | (50 , 60] | (60 , 70] |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
则样本在(10 , 50)上的频率为 ( ) (A)
.
(B)
. (C)
. (D)
.
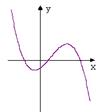8、若函数f(x)=
的图象如图所示，则一定有（ ）
A a<0 b>0 c>0 d<0
B a<0 b<0 c>0 d<0
C a<0 b>0 c<0 d<0
D a<0 b<0 c<0 d<0
9、有80个数，其中一半是奇数，一半是偶数，从中任取两数，则所取的两数和为偶数的概率为 (
) (A) 
. (B)
. (C) . (D)
.
10、设{an}是等差数列，从{a1，a2，a3，··· ，a20}中任取3个不同的数，使这三个数仍成等差数列，则这样不同的等差数列最多有（ ）
(A)90个 . (B)120个. (C)180个. (D)200个.
二、填空题：本大题共4小题，每小题4分，共16分。
11、设
的展开式的各项系数之和为M，且二项式系数之和为N，M—N=992，则展开式中x2项的系数为 ．
12、已知直线m、n及平面
，其中m∥n，那么在平面内到两条直线m、n距离相等的点的集合可能是：（1）一条直线；（2）一个平面；（3）一个点；（4）空集．
其中正确的是 ．
13、2女3男共5个小孩站成一排，其中2个女孩必须站在两端，则不同的排法共有 种.
14、一班级有学生50人，其中男生30人，女生20人。为了了解50名学生与身体状况有关的某项指标，今决定采用分层抽样的方法，抽取一个容量为20的样本，则女生张某被抽中的概率是 。
三、解答题：本大题共6小题，共84分，解答应写出文字说明、证明过程或演算步骤。
15、排球比赛的规则是5局3胜制，A、B两队每局比赛获胜的概率分别为
和
．
（Ⅰ）前2局中B队以2:0领先，求最后A、B队各自获胜的概率；
（Ⅱ）B队以3:2获胜的概率．
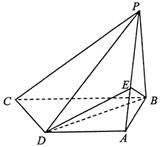16、如图，四棱锥P—ABCD中，PB⊥底面ABCD，CD⊥PD．底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3．点E在棱PA上，且PE=2EA．
（Ⅰ）求异面直线PA与CD所成的角；
（Ⅱ）求证：PC∥平面EBD；
（Ⅲ）求二面角A—BE—D的大小．
|
.
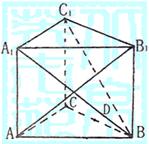
（1）求异面直线AB1与C1B所成的角；
（2）求点D到平面ACC1的距离；
（3）判断A1B与平面ADC1的位置关系，并证明你的结论.
18、某厂生产某种产品的固定成本（固定投入）为2500元，已知每生产x件这样的产
品需要再增加可变成本
（元），若生产出的产品都能以每件500元
售出，要使利润最大，该厂应生产多少件这种产品？最大利润是多少？
19、A袋中有1张10元1张5元的钱币，B袋中有2张10元1张5元的钱币，从A袋中任取一张钱币与B袋任取一张钱币互换，这样的互换进行了一次.
求（1）A袋中10元钱币恰是一张的概率；（2）A袋中10元钱币至少是一张的概率.
20、
，在区间
上的最大值与最小值，其中
。
06届高三数学第一轮模拟试卷一
参考答案：1、B 2、C 3、C 4、C 5、B 6、C7、D8、A9、A10、C
11、—250 12、（1）（2）（4）13、12 14、
15、解：排球比赛过程可以看成一个n次独立重复试验，
（Ⅰ）设最后A获胜的概率为
设最后B获胜的概率为
………………………………………………………… 4分
…………………… 6分
（Ⅱ）设B队以3:2获胜的概率为
．……………… 12分
16、⑴60°⑵略 ⑶
17、解：（1）取CB的中点D，则
.
故AB1在面CBB1C1上的射影为B1D.
在矩形CBB1C1中，
∽△DBB1.
故
由三垂线定理知，
所成角为
（4分）
（2）取AC的中点E，则
. 取CE的中点F，则DF//BE.
于是DF⊥面ACC1，故DF为D到面ACC1的距离.
（8分）
（3）设A1C与AC1交于点G，则G是A1C的中点.
又D是BC的中点，
（12分）
18、解：设该厂生产x件这种产品的利润为L（x）元，则
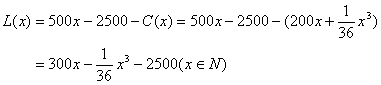（5分）
令
（8分）
又当
得极大值点.
当x=60时，L(x)=9500元.
因此，要使利润最大，该厂应生产60件这种产品，最大利润为9500元.（12分）
19、解： （1）A中2张钱币取1张，有2种情况，
B中3张钱币取1张，有3种情况，
∴互换一次有2´3 = 6种情况，
其中10元币恰是一张的情况有3种，
∴A袋中10元钱币恰是一张的概率为P1
=
.答略
（2）A袋中恰有一张10元币的概率为P1 = ；
A袋中恰有两张10元币的概率为P2 = 
；
∴ A袋中10元钱币至少是一张的概率P =
P1 + P2 = + = 
.
另解：. A袋中恰有0张10元币的概率为P0 = 
，
∴A袋中10元钱币至少是一张的概率P = 1 – P0 = .答略.
20、解：
（2'）
又
) （6'）
=
（8'）
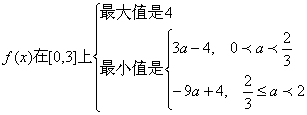
所以，最大值只可能是
再比较
最大值是
最小值只能是
故当
在[0，3]的最小值是
当
时，
（12'）