江苏省天一中学2006届高三数学模拟卷（7）
一、选择题：本大题共11小题，每小题5分，共55分. 在每小题给出的4个选项中，只有一项是符合题目要求的.
1、集合A＝
，B＝
，若“
”是“
”的充分条件，则
的取值范围可以是 （ ）
A、
B、
C、
D、
2、已知m、n是两条不重合的直线，α、β、γ是三个两两不重合的平面，给出下列四个命题：①若
； ②若
；③若
；④若m、n是异面直线，
. 其中真命题是 （ ）
A．①和② B．①和③ C．③和④ D．①和④
3、函数
的反函数是 （ ）
A．
B．
C．
D．
4、若
，则
的取值范围是 （
）
A．
B．
C．
D．
5、在R上定义运算
若不等式
对任意实数
成立， 则 （ ）
A．
B．
C．
D．
6、若钝角三角形三内角的度数成等差数列，且最大边长与最小边长的比值为m，则m的范围是 （ ）
A．（1，2） B．（2，+∞） C．[3，+∞
D．（3，+∞）
7、若直线
按向量
平移后与圆
相切，则c的值（ ）
A．8或－2 B．6或－4 C．4或－6 D．2或－8
8、已知
是定义在R上的单调函数，实数
，
，若
，则 （ ）
A．
B．
C．
D．
9、已知双曲线的中心在原点，离心率为
.若它的一条准线与抛物线
的准线重合，则该双曲线与抛物线的交点到原点的距离是 （ ）
A．2+
B．
C．
D．21
10、一给定函数的图象在下列图中，并且对任意
，由关系式
得到的数列
满足
，则该函数的图象是 （ ）
 |
A B C D
11、设定义域为R的函数
，则关于x的方程
有7个不同实数解的充要条件是
( )
(A)b<0且c>0 (B) b>0且c<0 (C)b<0且c=0 (D)b≥0且c=0
二、填空题：本大题共7小题，每小题4分，共28分.把答案填在题中横线上.
12、
的展开式中常数项是
.
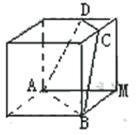
13、如图，正方体的棱长为1，C、D分别是两条棱的中点， A、B、M是顶点，那么点M到截面ABCD的距离是 .
14、设函数f(x)的图象关于点（1,2）对称，且存在反函数
，f (4)＝0，则
＝ .
15、某班有50名学生，其中 15人选修A课程，另外35人选修B课程．从班级中任选两名学生,他们是选修不同课程的学生的慨率是 ．(结果用分数表示)
16、直角坐标平面xoy中，若定点A(1,2)与动点P(x，y)满足
=4。则点P的轨
迹方程是 ．
17、函数f(x)=sinx+2
，x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点，则k的取值范围是
．
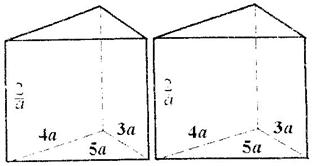
18、有两个相同的直三棱柱，高为
，底面三角形的三边长分别为3a、4a、5a(a>0)。用它们拼成一个三棱柱或四棱柱，在所有可能的情况中，全面积最小的是一个四棱柱，则a的取值范围是
．
三、解答题：本大题共5小题，共67分. 解答应写出文字说明，证明过程或演算步骤.
19、（本小题满分12分）已知在△ABC中，sinA（sinB＋cosB）－sinC＝0，sinB＋cos2C＝0，求角A、B、C的大小.
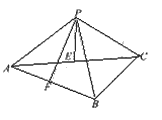20、（本小题满分13分）已知三棱锥P—ABC中，E、F分别是AC、AB的中点，△ABC，△PEF都是正三角形，PF⊥AB.
（Ⅰ）证明PC⊥平面PAB；
（Ⅱ）求二面角P—AB—C的平面角的余弦值；
（Ⅲ）若点P、A、B、C在一个表面积为12π的
球面上，求△ABC的边长.
21、（本小题满分14分）对定义域分别是
、
的函数
、
，规定：函数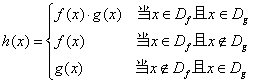
（1）若函数
，
，写出函数
的解析式；
（2）求问题(1)中函数的值域。
22、（本小题满分14分）已知椭圆C：
＋
＝1（a＞b＞0）的左．右焦点为F1、F2，离心率为e. 直线l：y＝ex＋a与x轴．y轴分别交于点A、B，M是直线l与椭圆C的一个公共点，P是点F1关于直线l的对称点，设
＝λ
.
（Ⅰ）证明：λ＝1－e2； （Ⅱ）确定λ的值，使得△PF1F2是等腰三角形.
23、（本小题满分14分）已知正项数列
满足
，且
，求证：（1）
； （2）
。
答案：
一、选择题：
DDCCC BAABA C
二、填空题：
12、－160 13、
14、－2 15、
16、x+2y-4=0 17、1<k<3 18、0<a<
三、解答题：
19、
20、（1）提示：证
（2）
（3）
21、（1）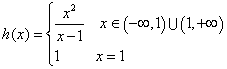
（2）(-∞,0]∪{1}∪[4,+∞)
22、（1）提示：利用＝λ，寻找
的关系式 （2）
23、（1）提示：利用，寻找
之间的不等关系式
（2）略证：
，
