第六讲 复习不等式
一、 本讲进度
《不等式》复习
二、本讲主要内容
1、不等式的概念及性质; 2、不等式的证明; 3、不等式的解法; 4、不等式的应用。
三、学习指导
1、不等式的性质是证明不等式和解不等式的基础。不等式的基本性质有:
(1)对称性或反身性:a>b![]() b<a;
b<a;
(2)传递性:若a>b,b>c,则a>c;
(3)可加性:a>b![]() a+c>b+c,此法则又称为移项法则;
a+c>b+c,此法则又称为移项法则;
(4)可乘性:a>b,当c>0时,ac>bc;当c<0时,ac<bc。
不等式运算性质:
(1)同向相加:若a>b,c>d,则a+c>b+d;
(2)正数同向相乘:若a>b>0,c>d>0,则ac>bd。
特例:(3)乘方法则:若a>b>0,n∈N+,则![]() ;
;
(4)开方法则:若a>b>0,n∈N+,则![]() ;
;
(5)倒数法则:若ab>0,a>b,则![]() 。
。
掌握不等式的性质,应注意:
(1)条件与结论间的对应关系,如是“![]() ”符号还是“
”符号还是“![]() ”符号;
”符号;
(2)不等式性质的重点是不等号方向,条件与不等号方向是紧密相连的。
2、均值不等式;利用完全平方式的性质,可得a2+b2≥2ab(a,b∈R),该不等式可推广为a2+b2≥2ab;或变形为ab≤![]() ;
;
当a,b≥0时,a+b≥![]() 或ab≤
或ab≤![]() .
.
在具体条件下选择适当的形式。
3、不等式的证明:
(1)不等式证明的常用方法:比较法,公式法,分析法,反证法,换元法,放缩法;
(2)在不等式证明过程中,应注重与不等式的运算性质联合使用;
(3)证明不等式的过程中,放大或缩小应适度。
4、 不等式的解法:
解不等式是寻找使不等式成立的充要条件,因此在解不等式过程中应使每一步的变形都要恒等。
一元二次不等式(组)是解不等式的基础,一元二次不等式是解不等式的基本题型。利用序轴标根法可以解分式及高次不等式。
含参数的不等式应适当分类讨论。
5、不等式的应用相当广泛,如求函数的定义域,值域,研究函数单调性等。在解决问题过程中,应当善于发现具体问题背景下的不等式模型。
用基本不等式求分式函数及多元函数最值是求函数最值的初等数学方法之一。
研究不等式结合函数思想,数形结合思想,等价变换思想等。
四、典型例题
例1、 已知f(x)=ax2-c,-4≤f(1)≤-1,-1≤f(2)≤5,试求f(3)的取值范围。
解题思路分析:
从条件和结论相互化归的角度看,用f(1),f(2)的线性组合来表示f(3),再利用不等式的性质求解。
设f(3)=mf(1)+nf(2)
∴ 9a-c=m(a-c)+n(4a-c)
∴ 9a-c=(m+4n)a-(m+n)c
∴
![]()
∴
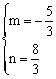
∴
f(3)=![]()
∵ -4≤f(1)≤-1,-1≤f(2)≤5
∴
![]() ≤
≤![]() ≤
≤![]() ,
,![]() ≤
≤![]() ≤
≤![]()
∴ -1≤f(3)≤20
说明:
1、本题也可以先用f(1),f(2)表示a,c,即a=![]() [f(2)-f(1)],c=
[f(2)-f(1)],c=![]() [f(2)-4f(1)],然后代入f(3),达到用f(1),f(2)表示f(3)的目的。
[f(2)-4f(1)],然后代入f(3),达到用f(1),f(2)表示f(3)的目的。
2、本题典型错误是从-4≤a-c≤-1,-1≤4a-c≤5中解出a,c的范围,然后再用不等式的运算性质求f(3)=9a-c的范围。错误的原因是多次运用不等式的运算性质时,不等式之间出现了不等价变形。
2、本题还可用线性规划知识求解。
例2、 设a>0,b>0,求证:![]() ≥
≥![]() 。
。
解题思路分析:
法一:比差法,当不等式是代数不等式时,常用比差法,比差法的三步骤即为函数单调性证明的步骤。
左-右=![]()
![]() ≥0
≥0
∴ 左≥右
法二:基本不等式
根据不等号的方向应自左向右进行缩小,为了出现右边的整式形式,用配方的技巧。
∵
![]() ≥
≥![]()
![]() ≥
≥![]()
∴
两式相加得:![]() ≥
≥![]()
例3、 设实数x,y满足y+x2=0,0<a<1,求证:![]() ≤
≤![]() 。
。
解题思路分析:
∵
![]() ≥
≥![]() ,
,![]() ≤
≤![]() ,0<a<1
,0<a<1
∴
![]() ≥
≥![]()
∴
![]() ≥
≥![]()
∴
![]() ≤
≤![]()
说明:本题在放缩过程中,利用了函数的单调性,函数知识与不等式是紧密相连的。
例4、已知a,b为正常数,x,y为正实数,且![]() ,求x+y的最小值。
,求x+y的最小值。
解题思路分析:
法一:直接利用基本不等式:![]() ≥
≥![]() 当且仅当
当且仅当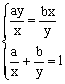 ,即
,即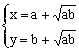 时等号成立
时等号成立
说明:为了使得等号成立,本题利用了“1”的逆代换。
法二:消元为一元函数
途径一:由![]() 得
得![]()
∴
![]()
∵ x>0,y>0,a>0
∴
由![]() >0得y-b>0
>0得y-b>0
∴
x+y≥![]()
当且仅当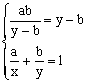 ,即
,即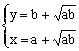 时,等号成立
时,等号成立
途径二:令![]() ,
,![]() ,
,![]() ∈(0,
∈(0,![]() )
)
∴
![]() ,
,![]()
∴
x+y=![]() ≥
≥![]()
当且仅当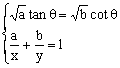 时,等号成立
时,等号成立
说明:本题从代数消元或三角换元两种途径起到了消元作用。
例5、已知f(x)=-3x2+a(6-a)x+b
(1)解关于a的不等式f(1)>0;
(2)当不等式f(x)>0的解集为(-1,3)时,求实数a,b的值。
解题思路分析:
(1)f(1)=-3+a(6-a)+b=-a2+6a+b-3
∵ f(1)>0
∴ a2-6a+3-b<0
△=24+4b
当b≤-6时,△≤0
∴ f(1)>0的解集为φ;
当b>-6时,![]()
∴
f(1)>0的解集为![]()
(2)∵ 不等式-3x2+a(6-a)x+b>0的解集为(-1,3)
∴ f(x)>0与不等式(x+1)(x-3)<0同解
∵ 3x2-a(6-a)x-b<0解集为(-1,3)
∴
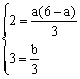
解之得![]()
例6、设a,b∈R,关于x方程x2+ax+b=0的实根为α,β,若a+b<1,求证:
α<1,β<1。
解题思路分析:
在不等式、方程、函数的综合题中,通常以函数为中心。
法一:令f(x)=x2+ax+b
则 f(1)=1+a+b>1-(a+b)>1-1=0
f(-1)=1-a+b>1-(a+b)>0
又∵ 0<a≤a+b<1
∴ -1<a<1
∴
![]()
∴ f(x)=0的两根在(-1,1)内,即α<1,β<1
法二:∵α+β=-a,αβ=b
∴ α+β+αβ=α+β<1
∴ α-β+αβ<α+β+αβ<1
∴(α-1)(β+1)<0
∵ β+1>0
∴ α<1
同理:β<1
说明:对绝对值不等式的处理技巧是适度放缩,如a-b≤a+b及b-a≤a±b的选择等。
例7、某人乘坐出租车从A地到乙地,有两种方案:第一种方案,乘起步价为10元,每km价1.2元的出租车;第二种方案,乘起步价为8元,每km价1.4元的出租车,按出租车管理条例,在起步价内,不同型号的出租车行驶的里路是相等的,则此人从A地到B地选择哪一种方案比较适合?
解题思路分析:
设A地到B地距离为mkm,起步价内行驶的路为akm
显然,当m≤a时,选起步价为8元的出租车比较合适
当m>a时,设m=a+x(x>0),乘坐起步价为10元的出租车费用为P(x)元,乘坐起步价为8元的出租车费用为Q(x)元,则P(x)=10+1.2x,Q(x)=8+1.4x
∵ P(x)-Q(x)=2-0.2x=0.2(10-x)
∴ 当x>0时,P(x)<Q(x),此时起步价为10元的出租车比较合适
当x<10时,P(x)>Q(x),此时选起步价为8元的出租车比较合适
当x=10时,此时两种出租车任选
五、同步练习
(一)选择题
1、“a>0且b>0”是“![]() ≥
≥![]() ”的
”的
A、充分而非必要条件 B、必要而非充要条件 C、充要条件 D、既非充分又非必要条件
2、设a<0,则关于x的不等式42x2+ax-a2<0的解集为
A、(![]() ) B、(
) B、(![]() ) C、(
) C、(![]() ) D、φ
) D、φ
3、若0<a<b且a+b=1,则四个数![]() ,b,2ab,a2+b2中最大的是
,b,2ab,a2+b2中最大的是
A、 ![]() B、b
C、2ab
D、a2+b2
B、b
C、2ab
D、a2+b2
4、已知x>0,f(x)=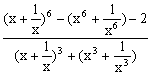 ,则
,则
A、f(x)≤2 B、f(x)≥10 C、f(x)≥6 D、f(x)≤3
5、已知![]() ,
,![]() (a>2),则
(a>2),则
A、 p>q B、p<q C、p≥q D、p≤q
6、若a-c<h, b-c<h,则下列不等式一定成立的是
A、 a-b<2h B、a-b>2h C、a-b<h D、a-b>h
7、关于x的方程9x+(a+4)·3x+4=0有解,则实数a的取值范围是
A、 (-∞,-8]∪[0,+∞) B、(-∞,-4)
B、 [-8,4) D、(-∞,-8]
8、若a>0,b>0,且2a+b=1,则S=2![]() -4a2-b2的最大值是
-4a2-b2的最大值是
A、 ![]() B、
B、![]() C、
C、![]() D、
D、![]()
(二)填空题
9、设a>0,b>0,a,b是常数,则当x>0时,函数f(x)=![]() 的最小值是______。
的最小值是______。
10、周长为![]() 的直角三角形面积的最大值为__________。
的直角三角形面积的最大值为__________。
11、记S=![]() ,则S与1的大小关系是__________。
,则S与1的大小关系是__________。
12、不等式x2-2x+3<3x-1的解集为__________。
(三)解答题
13、要使不等式![]() ≤
≤![]() 对所有正数x,y都成立,试问k的最小值是多少?
对所有正数x,y都成立,试问k的最小值是多少?
14、解关于x的不等式![]()
15、已知a≠0,求证:![]() ≥
≥![]()
16、已知不等式![]() 对n∈N+都成立,试求实数a的取值范围。
对n∈N+都成立,试求实数a的取值范围。
17、若a是正实数,2a2+3b2=10,求![]() 的最值。
的最值。
18、商店经销某商品,年销售量为D件,每件商品库存费用为I元,每批进货量为Q件,每次进货所需费用为S元,现假定商店在卖完该货物时立即进货,使库存量平均为![]() 件,问每批进货量Q为多大时,整个费用最省?
件,问每批进货量Q为多大时,整个费用最省?
参考答案
(一) 选择题
1、A 2、A 3、B 4、C 5、A 6、A 7、D 8、A
(二) 填空题
9、![]() 10、
10、![]() 11、S<1 12、(1,4)
11、S<1 12、(1,4)
(三) 解答题
13、![]()
14、当a≤-1时,x∈(-∞,a)∪(-1,2)
当-1<a<2时,x∈(-∞,-1)∪(a,2)
当a=2时,x∈(-∞,-1)
当a>2时,x∈(-∞,-1)∪(2,a)
15、当a≤b时,不等式显然成立
当a>b时,
左=![]() ≥
≥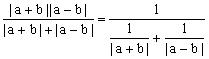 ≥
≥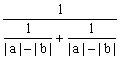
=![]()
16、![]() 或
或![]()
17、![]() ,此时
,此时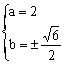
18、![]()