![]()
高一数学平面向量期末复习试题(必修4)
 (共160分,考试时间120分钟 ) 得分:
(共160分,考试时间120分钟 ) 得分:
一、填空题(本大题共14小题,每小题5分,共70分,请将答案写在横线处)1.若有以下命题:
① 两个相等向量的模相等;
② 若![]() 和
和![]() 都是单位向量,则
都是单位向量,则![]() ;
;
③ 相等的两个向量一定是共线向量; ④ ![]() ,
,![]() ,则
,则![]() ;
;
⑤ 零向量是唯一没有方向的向量; ⑥ 两个非零向量的和可以是零。
其中正确的命题序号是 。
2. 在水流速度为4![]() 的河流中,有一艘船沿与水流垂直的方向以8
的河流中,有一艘船沿与水流垂直的方向以8![]() 的速度航行,则船自身航行速度大小为____________
的速度航行,则船自身航行速度大小为____________![]() 。
。
3. 任给两个向量![]() 和
和![]() ,则下列式子恒成立的有________________。
,则下列式子恒成立的有________________。
① ![]() ②
② ![]()
③![]() ④
④ ![]()
4. 若![]() ,
,![]() 且
且![]() ,则四边形
,则四边形![]() 的形状为________。
的形状为________。
5.梯形![]() 的顶点坐标为
的顶点坐标为![]() ,
,![]() ,
,![]() 且
且![]() ,
,![]() ,则点
,则点![]() 的坐标为___________。
的坐标为___________。
6. ![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() ,若
,若![]() 是
是![]() 的重心,则
的重心,则![]() 点的坐标为__________,
点的坐标为__________,![]() __________________。
__________________。
7. 若向量![]() ,
,![]() ,
,![]() ,则
,则![]() ___________(用
___________(用![]() 和
和![]() 表示)。
表示)。
8. 与向量![]() 平行的单位向量的坐标为 ________________。
平行的单位向量的坐标为 ________________。
9. 在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,则
,则![]() ________________。
________________。
10.设![]() ,
,![]() ,若
,若![]() 与
与![]() 的夹角为钝角,则
的夹角为钝角,则![]() 的取值范围是 __ ____。
的取值范围是 __ ____。
11. 直线![]() 平行于向量
平行于向量![]() ,则直线
,则直线![]() 的斜率为____________。
的斜率为____________。
12. 已知![]() ,
,![]()
![]() ,则
,则![]() 的取值范围是 _________。
的取值范围是 _________。
13.已知向量![]() 、
、![]() 不共线,且
不共线,且![]() ,则
,则![]() 与
与![]() 的夹角为 __________。
的夹角为 __________。
14.在![]() 中
中![]() ,
,![]() ,
,![]() ,则下列推导正确的是__ _ 。
,则下列推导正确的是__ _ 。
① 若![]() 则
则![]() 是钝角三角形
② 若
是钝角三角形
② 若![]() ,则
,则![]() 是直角三角形
是直角三角形
③ 若![]() ,
则
,
则![]() 是等腰三角形
④ 若
是等腰三角形
④ 若![]() ,则
,则![]() 是直角三角形
⑤ 若
是直角三角形
⑤ 若![]() ,则△ABC是正三角形
,则△ABC是正三角形
二、解答题(本大题共6小题,共90分,请在答题卷指定区域内作答,解答应写出文字说明、证明过程或演算步骤)
15.已知![]() 且
且![]() ,
,![]() ,
,![]()
计算 ![]()
16设![]() 、
、![]() 、
、![]() 分别是
分别是![]() 的边
的边![]() 、
、![]() 、
、![]() 上的点,且
上的点,且![]()
![]() ,
,![]() ,若记
,若记![]() ,
,![]() ,试用
,试用![]() ,
,![]() 表示
表示![]() 、
、![]() 、
、![]() 。
。
17. 已知![]() ,
,![]() ,且
,且![]() 与
与![]() 夹角为120°求
夹角为120°求
⑴![]() ; ⑵
; ⑵![]() ; ⑶
; ⑶![]() 与
与![]() 的夹角。
的夹角。
18. 已知向量![]() =
=![]() ,
,![]() =
=![]() 。
。
⑴求![]() 与
与![]() ;⑵ 当
;⑵ 当![]() 为何值时,向量
为何值时,向量![]() 与
与![]() 垂直?
垂直?
⑶ 当![]() 为何值时,向量
为何值时,向量![]() 与
与![]() 平行?并确定此时它们是同向还是反向?
平行?并确定此时它们是同向还是反向?
![]() 19. 已知
19. 已知![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,设
,设![]() 是直线
是直线![]() 上一点,
上一点,![]() 是坐标原点
是坐标原点
⑴求使![]() 取最小值时的
取最小值时的![]() ;
⑵对(1)中的点
;
⑵对(1)中的点![]() ,求
,求![]() 的余弦值。
的余弦值。
20. 在![]() 中,
中,![]() 为中线
为中线![]() 上的一个动点,若
上的一个动点,若![]()
求:![]() 的最小值。
的最小值。
![]() 江苏省沛县湖西中学2007-2008第二学期期末复习试题
江苏省沛县湖西中学2007-2008第二学期期末复习试题
第二章平面向量参考答案
一.填空题:
1.①④;2.![]() ;3.②③;4.等腰梯形;5.(4,2);6.
;3.②③;4.等腰梯形;5.(4,2);6.![]() ,
,![]() ;7.
;7.![]() ;8.
;8.![]() 或
或![]() ;89.
;89.![]() ;10.
;10.![]() ;11.
;11.![]() ;12.
;12.![]() ;13.
;13.![]() ;14②③④⑤.
;14②③④⑤.
二.解答题:
15.因为![]() ,
,
由![]() ,所以
,所以![]() ,
,![]() .
.
16.由题意可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ;
;
![]() ;
;![]() .
.
17.由题意可得![]() ,
,![]() ,
,![]()
(1)![]() ;
;
(2)![]()
![]()
(3)设![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则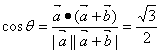 ,又
,又![]() ,所以
,所以![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() 。
。
18.因为![]() 所以
所以![]() ,
,![]() ,
,![]() ,
,
(1)![]() ,
, ![]() ;
;
(2)当向量![]() 与
与![]() 垂直时,则有
垂直时,则有![]()
![]() ,
,![]() ,即
,即![]() 解得
解得![]() 所以当
所以当![]() 时,向量
时,向量![]() 与
与![]() 垂直;
垂直;
(3)当向量![]() 与
与![]() 平行时,则存在
平行时,则存在![]() 使
使![]() 成立,于是
成立,于是![]() 解得
解得![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 时向量
时向量![]() 与
与![]() 平行且它们同向.
平行且它们同向.
19.(1)设![]() ,则
,则![]() ,由题意可知
,由题意可知![]() 又
又![]() 。所以
。所以![]() 即
即![]() ,所以
,所以![]() ,
,
则![]() ,当
,当![]() 时,
时,![]() 取得最小值,此时
取得最小值,此时![]() ,即
,即![]() 。
。
(2)因为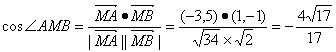 。
。
20.因为![]() ,
,![]() ,又
,又![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() 即
即![]() 为
为![]() 的中点时,
的中点时,![]() 取得最小值且为
取得最小值且为![]() 。
。