必修4第二章《平面向量》
一、选择题
1．在矩形ABCD中，O是对角线的交点，若
= （ ）
A．
B．
C．
D．
2．化简
的结果是 （ ）
A．
B．
C．
D．
3．对于菱形ABCD，给出下列各式：
①
②
③
④
2
其中正确的个数为 （ ）
A．1个 B．2个 C．3个 D．4个
4．在 ABCD中，设
，则下列等式中不正确的是（ ）
A．
B．
C．
D．
5．已知向量
反向，下列等式中成立的是 （ ）
A．
B．
C．
D．
6．已知平行四边形三个顶点的坐标分别为（－1，0），（3，0），（1，－5），则第四个点的坐标为 （ ）
A．（1，5）或（5，－5） B．（1，5）或（－3，－5）
C．（5，－5）或（－3，－5） D．（1，5）或（－3，－5）或（5，－5）
7．下列各组向量中：①
②
③
其中能作为表示它们所在平面内所有向量的基底的是 （ ）
A．① B．①③ C．②③ D．①②③
8．与向量
平行的单位向量为 （ ）
A．
B．
C．
或 D．
9．若
，
，则的数量积为 （ ）
A．10
B．－10 C．10
D．10
10．若将向量
围绕原点按逆时针旋转
得到向量
,则的坐标为( ）
A．
B．
C．
D．
11．设k∈R，下列向量中，与向量
一定不平行的向量是 （ ）
A．
B．
C．
D．
12．已知
，且
，则的夹角为 （ ）
A．60° B．120° C．135° D．150°
二、填空题
13．非零向量
，则
的夹角为
.
14．在四边形ABCD中，若
,则四边形ABCD的形状是
15．已知
，
，若
平行，则λ=
.
16．已知
为单位向量，
=4，
的夹角为
，则
方向上的投影为
.
三、解答题
17．已知非零向量满足,求证: 
18．已知在△ABC中，
，
且△ABC中∠C为直角，求k的值.
19、设
是两个不共线的向量，
，若A、B、D三点共线，求k的值.
20．已知
,的夹角为60o,
,
,当当实数
为何值时，⑴
∥
⑵
21．如图，ABCD为正方形，P是对角线DB上一点，PECF为矩形，
求证：①PA=EF；
|
22．如图，矩形ABCD内接于半径为r的圆O，点P是圆周上任意一点，
|
参考答案
一．选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | C | B | C | D | A | C | A | B | C | B |
二、填空题：
13． 120°； 14． 矩形 15、 
16． 
三、解答题：
17．证：
18．解：
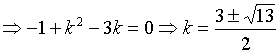
19．
若A，B，D三点共线，则
共线，
即
由于
可得：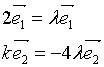 
故
20.⑴若∥ 得
⑵若得
21.解以D为原点
为x轴正方向建立直角坐标系
则A(0,1), C:(1,0) B:(1,1)
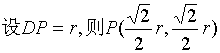
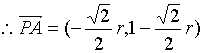
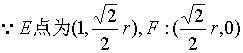
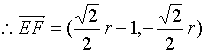
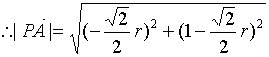
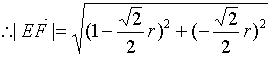
故
22.证:
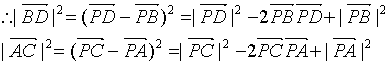
即