姓名_______ 湖南省省级示范性高中……洞口三中数学测试 (内容：必修一、二、三、四)
班次_____ 学号_______ 命题 方锦昌 易传庚
一:选择题(50分)
1. 函数
（
是以
为底的对数）的零点落在区间( )
A．（2，2.25） B．（2.25，2.5） C．（2.5，2.75） D．（2.75，3）
2. 函数
，
的递增区间是( )
A. 
B.
C.
D. 
3．下列命题中，错误的个数有( )个
①．平行于同一条直线的两个平面平行. ②．平行于同一个平面的两个平面平行.
③．一个平面与两个平行平面相交，交线平行. ④．一条直线与两个平行平面中的一个相交，则必与另一个平面相交.
A 0个 B 1个 C 2个 D 3个
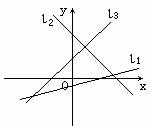
4．若图中直线
的斜率分别为k1,k2,k3,则有（
）
A. k2<k1<k3 B.k3<k2<k1 C. k2<k3<k1 D. k1<k3<k2
5．已知两直线
与
互相 平行，则
等于（ ）
A． 
B．
C．
D．
6．设偶函数f（x）的定义域为R，当
时f（x）是增函数，则
的大小关系是（ ） （A）
＞
＞
（B）＞＞
（C）＜＜
（D）＜＜
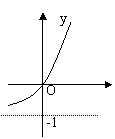
7．函数
的反函数的图象是（ ）
A．
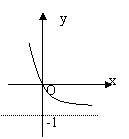
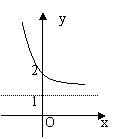
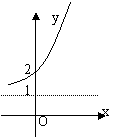
B．
C．
D．
|
8．假设一部机器在一天内随机发生一次故障，那么在晚上8点到11点内出故障的概率是（ ） A、
B、
C、
D、
9、
的最大值为（ ）
A、 B、
C、1
D、2
10、已知
且
若
，
则
的值为（ ）A、6 B、
C、3 D、
二:填空题
11、阅读右面的流程图，输出max的含义是_______
12. 给出函数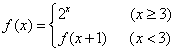
,则
；
13．函数
的定义域为
.
14．某小组有三名女生，两名男生，现从这个小组中任意选出一名组长，则其中一名女生小丽当选为组长的概率是___________。
15．已知
为不垂直的异面直线，
是一个平面，则在上的射影有可能是：
① 两条平行直线； ②两条互相垂直的直线；③ 同一条直线； ④一条直线及其外一点；在上面的结论中，正确结论的编号是 （写出所有正确结论的编号）
三：解答题
16、（08北京卷1题13分）．已知函数
（
）的最小正周期为
．（Ⅰ）求
的值；（Ⅱ）求函数
在区间
上的取值范围．
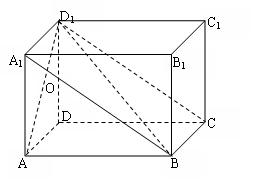17．(本小题满分14分)
在长方体ABCD-A1B1C1D1中，AB=
，B1B=BC=1，
（1）求D D1与平面ABD1所成角的大小；
（2）求面B D1C与面A D1D所成二面角的大小；
（18） 商场销售某一品牌的羊毛衫，购买人数是羊毛衫标价的一次函数，标价越高，购买人数越少。把购买人数为零时的最低标价称为无效价格，已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/ 件，商场以高于成本价的相同价格（标价）出售. 问：
（Ⅰ）商场要获取最大利润，羊毛衫的标价应定为每件多少元？ （Ⅱ）通常情况下，获取最大利润只是一种“理想结果”，如果商场要获得最大利润的75%，那么羊毛衫的标价为每件多少元？
19、已知曲线C：x2+y2-2x-4y+m=0 （1）当m为何值时，曲线C表示圆；（2）若曲线C与直线x+2y-4=0交于M、N两点，且· = 0 (O为坐标原点)，求m的值。
20、甲盒中有一个红色球，两个白色球，这3个球除颜色外完全相同，有放回地连续抽取2个，每次从中任意地取出1个球，用列表的方法列出所有可能结果，计算下列事件的概率。
（1）取出的2个球都是白球； （2）取出的2个球中至少有1个白球
21．（14分）已知定义域为
的函数同时满足以下三个条件：
[1] 对任意的
，总有
；[2] 
；[3] 若
，
，且
，则有
成立，并且称为“友谊函数”，请解答下列各题： (1)、若已知为“友谊函数”，求
的值； (2)、函数
在区间上是否为“友谊函数”？并给出理由. (3)已知为“友谊函数”，假定存在
，使得
且
， 求证：
.
参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| C | C | B | A | C | A | A | B | C | B |
11: a、b、c中的最大值 12: 8 13:（0，1） 14: 15:① ② ④
16 ¦(x)
．
因为函数的最小正周期为，且，所以
，解得
．（Ⅱ）由（Ⅰ）得
．因为
，所以
，所以
，因此
，即的取值范围为
．
17解：（1）连接A1D交AD1于O，∵ABCD-A1B1C1D1为长方体，而B1B=BC，则四边形A1ADD1为正方形，∴A1D^AD1，又∵AB^面A1ADD1，A1D
面A1ADD1，∴AB^A1D，∴A1D^面ABD1，
∴ÐDD1O是D D1与平面ABD1所成角， ∵四边形A1ADD1为正方形，∴ÐDD1O=450，则D D1与平面ABD1所成角为450．（2）连接A1B，∵A1A^面D1DCC1，D1D、DC面D1DCC1，∴A1A^ D1D、A1A^DC， ∴ÐDD1C是面B D1C与面A D1D所成二面角的平面角，在直角三角形D1DC中，∵DC=AB=，D1D=B1B =1，∴ÐDD1C=600，即面B D1C与面A D1D所成的二面角为600．
18解：（Ⅰ）设购买人数为n人，羊毛衫的标价为每件x元，利润为y元，则
∵k＜0，∴x=200时，ymax= - 10000k，即商场要获取最大利润，羊毛衫的标价应定为每件200元.
（Ⅱ）由题意得，k（x-
100）（x- 300）= - 10000k·75% 
所以,商场要获取最大利润的75%,每件标价为250元或150元.
19解：（1）由D2+E2-4F=4+16-4m=20-4m>0，得m<5。
（2）设M(x1,y1),N(x2,y2)，由OM⊥ON得x1x2+ y1y2=0。
将直线方程x+2y-4=0与曲线C：x2+y2-2x-4y+m=0联立并消去y得
5x2-8x+4m-16=0，由韦达定理得x1+x2=
①,x1x2=
②，又由x+2y-4=0得y=
(4-x), ∴x1x2+y1y2=x1x2+(4-x1)· (4-x2)=
x1x2-( x1+x2)+4=0。将①、②代入得m=.
20 .解 (1) (2)
21解（1）取
得
， 又由
，得
（2）显然在上满足[1] 
；[2] 
.若，，且，则有
故满足条件[1]、[2]、[3]，所以为友谊函数.分
(3)由 [3]知任给
其中
，且有
，不妨设
则必有：
所以：
所以：
.依题意必有,
下面用反证法证明：假设
，则有
或
(1)
若，则
，这与矛盾； (2)若，则
，这与矛盾；
故由上述（1）、（2）证明知假设不成立，则必有，证毕.