必修2综合练习
一，选择题
1，直线2x-y=7与直线3x+2y-7=0的交点是（ ）
A ，(3,-1) B ，(-1,3) C ，(-3,-1) D ，(3,1)
2，直线
x－y+1=0的倾斜角为 ( )
A，150º B，120º C，60º D，30º
3，若Ａ（－２，３），Ｂ（３，－２），Ｃ（0，ｍ）三点共线，则ｍ的值为（ ）
Ａ，1 Ｂ，－1 Ｃ，－5 Ｄ，5
4，直线2x-3y+6=0与x轴的交点是A,与y轴的交点是B,O是坐标原点
则△AOB的面积是（ ）
A，６; B，３; C，１２; D，２.
5，右图所示的直观图，其原来平面图形的面积是（ ）
A，4 B.，4
C.，2 D.，8
6，两条平行线4x+3y-1=0与8x+6y+3=0之间的距离是（ ）
A， B， C， D，0.5
7，两直线
与
的位置关系（ ）
A，垂直 B，平行 C，重合 D，以上都不对
8，已知正方体外接球的体积是
，那么正方体的棱长等于 （ ）
（A）
（B）
（C）
（D）
9，直线3x+4y-13=0与圆
的位置关系是：（ ）
A. 相离; B. 相交; C. 相切; D. 无法判定.
10，经过点M（1，1）且在两轴上截距相等的直线是（ ）
A．x+y=2 B．x+y=1 C．x=1或y=1 D．x+y=2或x=y
11，过圆
上的一点（1，
）的圆的切线方程是（ ）
A，
B，
C，
D，
12, 两圆（x―2）2+(y+1)2 = 4与(x+2)2+(y―2)2 =16的公切线有（ ）
A．1条 B．2条 C．4条 D．3条
13，圆x2+y2+4x–4y+4=0关于直线l: x–y+2=0对称的圆的方程是（ ）
A．x2+y2=4 B．x2+y2–4x+4y=0
C．x2+y2=2 D．x2+y2–4x+4y–4=0
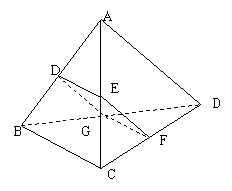
14，如下图，在三棱锥A-BCD中,E,F,G,H分别是边AB,AC,CD,BD的中点，且AD=BC，那么四边形EFGH是（ ）
A.平行四边形 B.矩形 C.菱形 D. 正方形
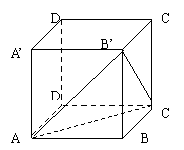
15，上图的正方体ABCD- A’B’C’D’中，它的棱长是a，则点Ｂ到平面ＡＢ’C的距离是（ ）
A. 
B.
C.
D. 
a
二、填空题
16，点A(1,3)关于点Ｐ(2,5)对称点Ａ＇的坐标是
17，已知A（-3，-5），B（5，1），则以线段AB为直径的圆的方程一般式为_______
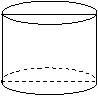
18，如下左图是一个底面直径和高都是4的圆柱的侧面积为 _____（最后的结果保留π）
19，光线从点（―1，3）射向x轴，经过x轴反射后过点（4，6），则反射光线所在的直线方程一般式是
20，已知
是直线，
是平面，下列命题中：
①若
垂直于
内两条直线，则
；②若平行于，则内可有无数条直线与平行；
③若
，则
；④若m⊥n，n⊥l则m∥l；
⑤若
，则
；正确的命题个数为____________。
三、解答题（请按照要求写清必要的步骤）
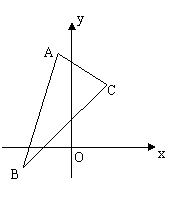
21，已知点
和直线l:
求：（1）过点P与直线l平行的直线方程一般式；
（2）过点P与直线l垂直的直线方程一般式；
 |
22，已知
三个顶点是
，
，
．
（Ⅰ）求BC边中线AD所在直线方程；
（Ⅱ）求点Ａ到ＢＣ边的距离．
23，求经过点A（0，4），B（4，6）且圆心在直线x―2y―2=0上的圆的方程;
24，已知直线:y=x+b和圆x2+y2+2x―2y+1=0（1）若直线和圆相切，求直线的方程;（2）若b=1，求直线和圆相交的弦长；
25，在四棱锥P―ABCD中，ＰD⊥平面ＡＢＣＤ，底面是边长是１的正方形，
侧棱ＰＡ与底面成４５０的角，Ｍ，Ｎ，分别是ＡＢ，ＰＣ，的中点；
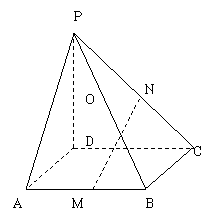（1）求证：ＭＮ∥平面ＰＡＤ；（2）求四棱锥P-ABCD的体积.
26，已知方程
表示一个圆，
（1）求实数m的取值范围；（2）求该圆半径r的取值范围；（3）求圆心的轨迹方程；
参考答案：
一、选择题 ACABA DADCD ABACA
二、填空题 16、（3，7）；17、x2+y2-2x+4y-20=0；18、16π；19、9x-5y-6=0；20、1
三、解答题 21、（1）3x+y+14=0(2)x+3y-2=0；22、(1)3x+y-1=0 (2)
；23、x2+y2-8x-2y-8=0；
24、（1）y=x+2±（2）；25、（1）略（2）1/3；26、（1）-1/7<m<1;(2)
;(3)y=4(x-3)2-1 (20/7<x<4)