高一数学新课程必修模块五结业测试卷
说明：本试卷满分100分，考试时间90分钟。学生答题时可使用学生专用计算器。
一、选择题（本大题共10小题，每小题4分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的）．
1．若
且
，则下列不等式中一定成立的是（
▲ ）
A．
B．
C．
D．
2．已知数列
，
,
…
，…，则
是这个数列的（ ▲ ）
A．第10项 B．第11项 C．第12项 D．第21项
3．若
的三角
，则A、B、C分别所对边
=（ ▲ ）
A．
B．
C．
D．
4．在等差数列
中，已知
，
，则
（ ▲ ）
A．9 B．12 C．15 D．18
5．直角坐标系内的一动点，运动时该点坐标满足不等式
，则这个动点的运动区域(用阴影表示)是（
▲ ）
 |
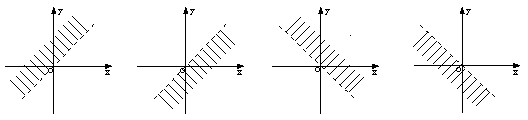A． B． C． D．
6．已知
，
是两个正数，则下列不等式中错误的是（ ▲ ）
A．
B．
C．
D．
7．在等比数列中，已知
，
，
，则
（ ▲ ）
A．4 B．5 C．6 D．7
8．在中，若
，则的形状一定是（ ▲ ）
A．锐角三角形 B．钝角三角形 C．直角三角形 D．等腰三角形
9．设关于
的不等式：
解集为
，若
，则实数的取值范围是（ ▲ ）
A．
B．
C．
D．
10．小明在玩投石子游戏，第一次走1米放2颗石子，第二次走2米放4颗石子…第
次走米放
颗石子，当小明一共走了36米时，他投放石子的总数是（ ▲ ）
A．36 B．254 C．510 D．512
二、填空题（本大题共7小题，每小题3分，满分21分）．
11．若
，
，则
的范围是__ ▲__ __。
12．三角A，B，C所对的边分别是3，4，6，则
____▲______。
13．等比数列
的公比为
，前5项和为31，则数列的首项为____▲______。
14．在中，
，
，
，则三角形ABC的面积为_____▲_____。
15．已知数列满足
，当
____▲______时，
。
16．已知实数，当，满足____▲______条件时，不等式
成立。
17．观察下面图形相应的点数，按照这样的规律，第七个图形的点数是____▲______。
答 卷 纸
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | ||||
| 得分 | |||||||||
一、选择题（本大题共10小题，每小题4分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的）．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题（本大题共7小题，每小题3分，满分21分）．
11． 12． 13． 14．
15． 16． 17．
三、解答题（本大题共5小题，满分39分．解答应写出文字说明．证明过程或演算步骤）．
18．（本题7分）已知数列的通项公式
。
（1）求
，
；
（2）若
，分别是等比数列
的第1项和第2项，求数列的通项公式
。
19．（本题8分）某餐馆一天中要购买A，B两种蔬菜，A、B蔬菜每斤的单价分别为2元和3 元。根据需要，A蔬菜至少要买6斤，B蔬菜至少要买4斤，而且一天中购买这两种蔬菜的总费用不能超过60元。
（1）写出一天中A蔬菜购买的斤数x和B蔬菜购买的斤数y之间的不等式组；
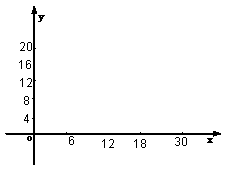（2）在下面给定的坐标系中画出（1）中不等式组表示的平面区域（用阴影表示），并求出它的面积。
20．（本题8分）如图，已知
，P、Q分别是
两边上的动点。
（1）当
，
时，求PQ的长；
（2）
，
长度之和为定值4，求线段PQ最小值。
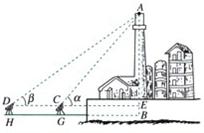
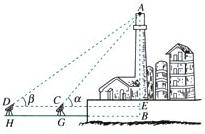21．（本题8分）如图，这是测量一座底部不可到达的高楼AB（A为最高点，B为底部）的测量方案示意图。DH、CG为量角仪，高度为1.35米，测得仰角
，
，又测得基线
米，请你计算该高楼的高度（精确到0.01米）。
22．（本题8分）某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元。同时，公司每年需要付出设备的维修和工人工资等费用，第一年各种费用2万元，第二年各种费用4万元，以后每年各种费用都增加2万元。
（1）引进这种设备后，第几年后该公司开始获利；
（2）这种设备使用多少年，该公司的年平均获利最大？
温州市部分学校2007年数学新课程必修模块五结业测试
参考答案
一、选择题（本大题共10小题，每小题4分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的）．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | C | A | A | C | B | D | C | C |
二、填空题（本大题共7小题，每小题3分，满分21分）．
11．
12．
13． 16 14．
15． 1 16．ab>0 或b>0或a<0 17． 28
三、解答题（本大题共5小题，满分39分．解答应写出文字说明．证明过程或演算步骤）．
18．（本题7分）已知数列的通项公式。
（1）求，；
（2）若，分别是等比数列的第1项和第2项，求数列的通项公式。
解：（1）
，
………………………………………3分
（2）由题意知：等比数列中，
，
公比
……………………………………5分
的通项公式
……………7分
19．（本题8分）某餐馆一天中要购买A，B两种蔬菜，A、B蔬菜每斤的单价分别为2元和3 元。根据需要，A蔬菜至少要买6斤，B蔬菜至少要买4斤，而且一天中购买这两种蔬菜的总费用不能超过60元。
（1）写出一天中A蔬菜购买的斤数x和B蔬菜购买的斤数y之间的不等式组；
（2）在下面给定的坐标系中画出（1）中不等式组表示的平面区域（用阴影表示），并求出它的面积。
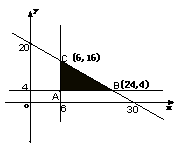解：（1）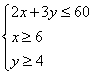
…………………3分
（2）画出的平面区域如右图，………………5分
A（6，4），由
求得C（6，16）
由
求得B（24，4）…………7分
………8分
20．（本题8分）如图，已知，P、Q分别是两边上的动点。
（1）当
，时，求PQ的长；
（2）AP、AQ长度之和为定值4，求线段PQ最小值。
解：（1）由余弦定理得
：
…………………3分
（2）设AP=x，AQ=y，则
………………4分
………………5分
……………………7分
当且仅当x=y时，即AP=BP=2时，PQ取到最小值，最小值是2。…………………8分
21．（本题8分）如图，这是测量一座底部不可到达的高楼AB（A为最高点，B为底部）的测量方案示意图。DH、CG为量角仪，高度为1.35米，测得仰角，，又测得基线米，请你计算该高楼的高度（精确到0.01）。
解：在三角形ACD中，
得：…2分
所以
（米）…4分
所以，
（米）…………………………6分
高楼的高度为：AB=38.46+1.35=39.81（米）……………………8分
22．（本题8分）某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元。同时，公司每年需要付出设备的维修和工人工资等费用，第一年各种费用2万元，第二年各种费用4万元，以后每年各种费用都增加2万元。
（1）引进这种设备后，第几年后该公司开始获利；
（2）这种设备使用多少年，该公司的年平均获利最大？
解：（1）由题意知，每年的费用是以2为首项，2为公差的等差数列，设纯收入与年数n的关系为f(n),则f(n)=21n-[2n+
]-25=20n-n2-25……………………2分
由f(n)>0得n2-20n+25<0
解得
又因为n
,所以n=2,3,4,……18.即从第2年该公司开始获利……………………4分
（2）年平均收入为
=20-
………………………………6分
当且仅当n=5时，年平均收益最大.所以这种设备使用5年，该公司的年平均获利最大。…8分
试卷结构情况
| 章节 | 内容 | 课时数 | 题型 | 分值 | 合计 | 综合 | ||
| 选择 | 填空 | 解答 | ||||||
| 正余弦定理 8课时 | 1．1正弦定理、余弦定理 | 3 | T3 | T12 |
| 10 | 25 | T20是余弦定理与均值不等式综合 T22是等差数列，一元二次不等式，均值不等式综合 |
| 1．2应用举例 | 4 | T8 | T14 | T21 | 15 | |||
| 1．3实习作业 | 1 |
|
| |||||
| 数列 共 12 课 时 | 2．1数列概念与简单表示 | 2 | T2 | T15 T17 |
| 7 | 30 | |
| 2．2等差数列 | 2 | T4 |
| T18（1） |
12 | |||
| 2．3等差数列的前n项和 | 2 |
| T22（1） | |||||
| 2．4等比数列 | 2 | T7 |
| T18（2） | 15 | |||
| 2．5等比数列的前n项和 | 2 | T10 | T13 |
| ||||
| 回顾与小结 | 2 |
|
|
| ||||
| 不等式 共 16 课 时 | 3．1不等关系（含不等式性质） | 2 | T1 | T11 T16 |
| 10 | 45 | |
| 3．2一元二次不等式及解法 | 3 | T9 |
| T22（1） | 11 | |||
| 3．3二元一次水等式（组）与简单线性规划问题 | 5 | T5 |
| T19 | 12 | |||
| 3．4基本不等式 | 3 | T6 |
| T20（2） T22（2） | 12 | |||
| 小结与复习 | 3 |
|
|
|
| |||