高一数学春期模块4结业考试试卷
时量:120分钟 满分:100分
| 得分 | 评卷人 |
一、选择题（本大题共10小题，每小题4分，共40分。每小题给
出的四个选项中，只有一项是符合题目要求的。）
1、
的值是 （ ）
A. 
B. 
C. 
D. 
2、函数
的周期是（ ）
A．
B．
C．2 D. 4
3、化简式子
的值是（ ）
A．
B．
C．
D．
4、如果点
位于第三象限，那么角
所在象限是（ ）
A． 第一象限 B． 第二象限
C． 第三象限 D． 第四象限
5、已知平面向量
，
，则向量
的坐标是（ ）
Ａ．
B．
Ｃ．
Ｄ．
6、将函数
图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），
再将所得的函数图象向左平移
个单位，最后所得到的图象对应的解析式是 （ ）
Ａ
B 
C 
D 
7、已知向量
，
，且
，则实数
的值为（ ）
A. 
B. 
C. 
D. 
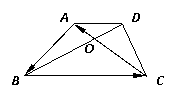8、如图，四边形ABCD是梯形，AD∥BC，则
等于( )
A．
B．
C．
D．
9、已知
，
，且
，则
的坐标为．（ ）
A．(1,2) 或(－1,－2) B．(－1,－2) C．(2,1) D．(1,2)
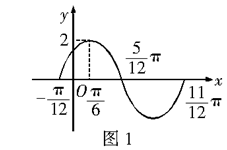
10、已知图1是函数
的图象上的一段，则（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
| 得分 | 评卷人 |
二、填空题（本大题共5小题，每小题3分，共15分，把答案填在题中横线上。）
11、若
，且
，则
的值是
；
12、设扇形的半径长为
，面积为
，则扇形的圆心角的弧度数是
；
13、已知
平行，则k的值为_________；
14、设
是以4为周期的函数,且当
时, 
,则
；
15、给出下列命题：
①、第二象限角是钝角；
②、
；
③、
；
④、若
是两个单位向量，则
；
⑤、若
则
或
；
其中正确的命题的序号是： ；
| 得分 | 评卷人 |
| 得分 | 评卷人 |
16、（本小题满分7分）
（1）、若
，且
是第三象限角，求
值；
（2）、若
，求
的值。
| 得分 | 评卷人 |
17、（本小题满分7分）
已知△
三个顶点的坐标分别为
，
，
．
（1）、若
，求
的值；
（2）、当c满足（1）问题的结论时，求△的重心坐标
.
18、（本小题满分7分）
（文科）、已知：
，求
与
的值；
（理科）、已知
，
，
，
，且
∥
，则求
的值.
| 得分 | 评卷人 |
19、（本小题满分8分）
已知向量满足
，且
。
（1）、求向量的坐标； （2）、求向量与
的夹角。
| 得分 | 评卷人 |
| 得分 | 评卷人 |
20、（本小题满分８分）
设
,
是两个不共线的非零向量，如果
，
，
.
（1）、试确定实数
的值，使的取值满足向量
与向量
共线；
（2）、证明：A、B、D三点共线．
21、（本小题满分８分）
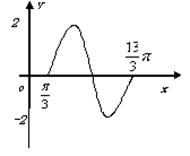函数
一段图象如图所示。
⑴、分别求出
并确定函数的解析式；
⑵、求出的单调递增区间；
⑶、指出当取得最大值和最小值时的集合．
湘钢二中2008年春期高一数学试卷(模块4结业考试)
数学必修4参考答案
一、选择题：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | D | A | B | D | C | D | B | A | D |
二、填空题：
11．
12． 
13．
14．
15． ③④
三、 解答题：
16．解：（1）∵
∴ 
-----------1分
∴ 
解得
----------2分
又∵是第三象限角
∴ 
-------3分
∴ 
-------4分
（2）∵
∴ 
-------6分
则
-------7分
17．解：（1）∵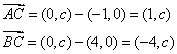 
--------2分
若
∴ 
即 
--------3分
解得 
-------4分
（2）、 若
则
-------6分
即 
-------7分
18．解：（（文科）∵
∴ 
---------2分
解得 
---------3分
∴ =
---------5分
把代入上式得
=
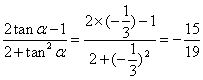---------7分
（理科）∵ ∥
∴ 
---------2分
∴ 
--------3分
∵
--------5分
把代入上式得
--------7分
19．解：（1）
因为 
则 
-------①
---------1分
又∵ 已知
，且
- -------2分
∴ 
-------② - -------3分
由①②解得 
∴
- -------4分
（2）设向量与的夹角
∵
- -------5分
∴ 
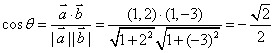- -------6分
或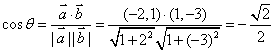
- -------7分
∵
∴向量与的夹角
- -------8分
20．（1）解： 若向量与向量共线
则存在实数
使得 
成立- -------2分
即
则 
解得 
- -------4分
（2） 证明：∵ 
- -------5分
又∵
∴ 
- -------6分
∴
又
有公共点
- -------7分
∴A、B、D三点共线 - -------8分
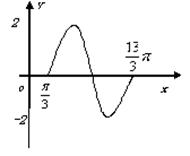20．解：（1）由图可知：
- -------1分
∵
∴ 
-
-------2分
∵图象过点
则
∴ 
又
则 
- -------3分
∴
-------4分
（2）又（1）知
故 
则 
- -------5分
故 的单调递增区间为 
- -------6分
（3） ∵
∴ 当
时即
即当 
时 
- -------7分
当
时即
即当 
时 
- -------8分