高一数学暑假作业一 直线与方程
一.填空题
1.过点![]() ,且斜率为2的直线方程是__________________________。
,且斜率为2的直线方程是__________________________。
2.过点![]() ,且在
,且在![]() 轴和
轴和![]() 轴上截距的绝对值相等的直线共有_____________条。
轴上截距的绝对值相等的直线共有_____________条。
3.已知![]() ,
,![]() 为坐标原点,点
为坐标原点,点![]() 在第三象限,若
在第三象限,若![]() 是以
是以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形,
则![]() 所在直线方程为___________________________。
所在直线方程为___________________________。
4.设![]() ,则直线
,则直线![]() 恒过定点__________________。
恒过定点__________________。
5.若AC<0,BC<0,则直线Ax+By+c=0不通过第_________象限。
6.(08年江苏)在平面直角坐标系中,设三角形![]() 的顶点分别为
的顶点分别为![]() ,点P(0,p)在线段AO上(异于端点),设
,点P(0,p)在线段AO上(异于端点),设![]() 均为非零实数,直线
均为非零实数,直线![]() 分别交
分别交![]() 于点
于点![]() ,一同学已正确算的
,一同学已正确算的![]() 的方程:
的方程:![]() ,请你写出
,请你写出![]() 的方程:( )
的方程:( )![]()
7.已知![]() ,
,![]() ,求过
,求过![]() 、
、![]() 的直线
的直线![]() 的方程________。
的方程________。
8.若直线![]() 过点(1,1)且与两坐标轴所围成的三角形面积为2,则这样的直线有_______条。
过点(1,1)且与两坐标轴所围成的三角形面积为2,则这样的直线有_______条。
9.一束光线从点![]() 射出,经
射出,经![]() 轴反射后,通过点
轴反射后,通过点![]() ,则反射光线所在直线的方程是____________________。
,则反射光线所在直线的方程是____________________。
10.点![]() 到直线
到直线![]() 的距离的最大值是 。
的距离的最大值是 。
二.解答题
11. 一条直线![]() 被两条直线
被两条直线![]() 和
和![]() 截得线段中点恰是坐标原点,求直线
截得线段中点恰是坐标原点,求直线![]() 的方程。
的方程。
12. 设直线![]() 的方程为
的方程为![]() 。
。
(1) 若![]() 在两坐标轴上的截距相等,求
在两坐标轴上的截距相等,求![]() 的方程;
的方程;
(2) 求证: 直线![]() 经过定点;并求出该定点的坐标;
经过定点;并求出该定点的坐标;
(3) 若![]() 不经过第二象限,求实数
不经过第二象限,求实数![]() 的取值范围。
的取值范围。
13. (1)直线从点A(2,1)射到x轴上的点P,经x轴反射后过点B(4,3),求点P的坐标、入射斜率和反射斜率。
(2)直线从点A(2,1)射到y轴上的点Q,经y轴反射后过点B(4,3),求点P的坐标、入射斜率和反射斜率。
14. 过点![]() 作直线
作直线![]() 分别交
分别交![]() 正半轴于
正半轴于![]() 两点
两点
(1)若![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程;
的方程;
(2)若![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程。
的方程。
暑假作业二 圆与方程
一.填空题
1.若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 有公共点,则直线
有公共点,则直线![]() 的斜率的取值范围为_____________。
的斜率的取值范围为_____________。
2.经过圆x2+2x+y2=0的圆心G,且与直线x+y=0垂直的直线方程是_____________。
3.原点到直线![]() 的距离为_____________。
的距离为_____________。
4. 若圆![]() 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线![]() 和
和![]() 轴相切,则该圆的标准方程是__________。
轴相切,则该圆的标准方程是__________。
5.直线![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() ,再向右平移1个单位,所得到的直线为_____________。
,再向右平移1个单位,所得到的直线为_____________。
6.直线![]() 与圆
与圆![]() 相切,则实数
相切,则实数![]() 等于 _____________。
等于 _____________。
7.若直线3x+4y+m=0与圆x2+y2-2x+4y+4=0没有公共点,则实数m的取值范围是 ________________。
8.已知直线![]() 与圆
与圆![]() ,则
,则![]() 上各点到
上各点到![]() 的距离的最小值为_____________。
的距离的最小值为_____________。
9.已知圆C: ![]() (a为实数)上任意一点关于直线l:x-y+2=0的对称点都在圆C上,则a=____________。
(a为实数)上任意一点关于直线l:x-y+2=0的对称点都在圆C上,则a=____________。
10. 过点A(0,3),被圆(x-1)2+y2=4截得的弦长为2的直线方程是 _____________。
二.解答题
11.求与圆![]() 外切,且与直线
外切,且与直线![]() 相切与点
相切与点![]() 的圆的方程。
的圆的方程。
12.在圆![]() 上任意取一点
上任意取一点![]() ,以
,以![]() 为圆心作圆与圆
为圆心作圆与圆![]() 的直径
的直径![]() 相切于点
相切于点![]() ,两圆相交于
,两圆相交于![]() 两点,求证:
两点,求证:![]() 平分
平分![]()
13.已知圆![]() ,直线
,直线![]() :
:![]()
(1)若![]() 与圆交于两个不同点
与圆交于两个不同点![]() ,求实数
,求实数![]() 的取值范围
的取值范围
(2)若![]() 的中点为
的中点为![]() ,
,![]() ,且
,且![]() 与
与![]() :
:![]() 的交点为
的交点为![]() ,
,
求证:![]() 为定值
为定值
14. 已知![]() ,直线
,直线![]() :
:![]() 和圆
和圆![]() :
:![]() .
.
(Ⅰ)求直线![]() 斜率的取值范围;
斜率的取值范围;
(Ⅱ)直线![]() 能否将圆
能否将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段圆弧?为什么?
的两段圆弧?为什么?
暑假作业三 点、线、面的位置关系
一、填空题
1.两个不重合的平面将空间分成 个部分.
2.已知![]() ,则直线
,则直线![]() 与A的位置关系用集合符号表示为 .
与A的位置关系用集合符号表示为 .
3.平面外一点和平面内一点的连线与这个平面内的任意一条直线的位置关系是 .
4.在三棱锥![]() 中,
中,![]() 分别是
分别是![]() 的重心,则平面
的重心,则平面![]() 和平面
和平面
![]() 的位置关系是 .
的位置关系是 .
5.给出四个命题:①平行于同一直线的两平面平行;②垂直于同一直线的两平面平行;③平行于同一平面的两平面平行;④垂直于同一平面的两平面平行.其中正确命题的序号有 .
6.在四面体![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() ,则平面
,则平面![]() 平面
.
平面
.
7.把等腰![]() 沿斜边
沿斜边![]() 上的高折成一个二面角后,若
上的高折成一个二面角后,若![]() ,则此二面角的大小为 .
,则此二面角的大小为 .
8. 已知正四棱锥![]() 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等,![]() 是
是![]() 的中点,则
的中点,则![]() 所成的角的余弦值为
.
所成的角的余弦值为
.
 9.
设直线
9.
设直线![]() 平面
平面![]() ,过平面
,过平面![]() 外一点
外一点![]() 与
与![]() 都成
都成![]() 角的直线的条数有且只有 .
角的直线的条数有且只有 .
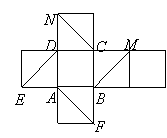
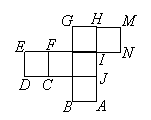
10.如图是正方体的平面展开图.在这个正方体中,
①![]() 与
与![]() 平行;②
平行;②![]() 与
与![]() 是异面直线;
是异面直线;
③![]() 与
与![]() 成
成![]() 角;④
角;④![]() 与
与![]() 垂直.
垂直.
以上四个命题中,正确命题的序号是 .
二、解答题
11.如图,三棱锥![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() 分别是
分别是![]() 上的点,且有
上的点,且有
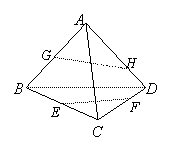
![]() 。试判断
。试判断![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
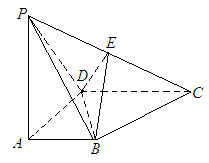 12.如图所示,
四棱锥P
12.如图所示,
四棱锥P ![]() ABCD底面是直角梯形,
ABCD底面是直角梯形, ![]() 底面ABCD, E为PC的中点, PA=AD=AB=1.
底面ABCD, E为PC的中点, PA=AD=AB=1.
(1)证明:
![]() ;(2)证明:
;(2)证明:
![]() ;
;
(3)求三棱锥B![]() PDC的体积V.
PDC的体积V.
13.如图,在直三棱柱ABC-A1B
求证:(1)C
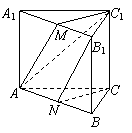
14.在正方体![]() 中,已知E、F、G分别是棱AB、AD、
中,已知E、F、G分别是棱AB、AD、![]() 的中点.
的中点.
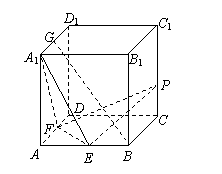 (1)求证:BG//平面
(1)求证:BG//平面![]() ;(2)若P为棱
;(2)若P为棱![]() 上一点,求当
上一点,求当![]() 等于多少时,平面
等于多少时,平面![]() 平面
平面![]() ?
?
暑假作业四 空间几何体及其表面积和体积
一、填空题
1.平行投影与中心投影之间的区别是____________ .
2.若长方体三个面的面积分别是![]() ,则长方体的体积等于 .
,则长方体的体积等于 .
3.用长、宽分别是![]() 与
与![]() 的矩形硬纸卷成圆柱的侧面,则圆柱的底面半径为___________ .
的矩形硬纸卷成圆柱的侧面,则圆柱的底面半径为___________ .
4.棱台上、下底面面积之比为![]() ,则棱台的中截面分棱台成两部分的体积之比是___________ .
,则棱台的中截面分棱台成两部分的体积之比是___________ .
5.若用半径为![]() 的半圆形铁皮卷成一个圆筒,则这个圆锥的高为___________ .
的半圆形铁皮卷成一个圆筒,则这个圆锥的高为___________ .
6.一个三角形在其直观图中对应一个边长为1正三角形,原三角形的面积为 .
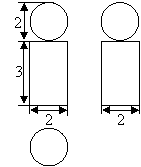 7.根据图中所给的图形制成几何体后,三点重合在一起是
.
7.根据图中所给的图形制成几何体后,三点重合在一起是
.
 |
第7题图
8.上右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是 .
9.把一个圆锥截成圆台,若圆台的上、下底面半径的比是![]() ,母线长
,母线长![]() ,则圆锥的母长为
,则圆锥的母长为
![]() .
.
10.一个直径为![]() 的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高
的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高![]() 则此球的半径
则此球的半径
为______ ![]() .
.
二、解答题
11.一个正四棱台形油槽可以装煤油![]() ,假如它的上、下底面边长分别为
,假如它的上、下底面边长分别为![]() 和
和![]() ,求它的深度。
,求它的深度。
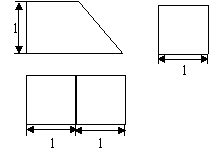 12.一几何体按比例绘制的三视图如图所示(单位:
12.一几何体按比例绘制的三视图如图所示(单位:![]() ).⑴试画出它的直观图;⑵求它的体积.
).⑴试画出它的直观图;⑵求它的体积.
13.设![]() 是球
是球![]() 表面上的四个点,
表面上的四个点,![]() 两两垂直,且
两两垂直,且![]() ,求球的体积与表面积.
,求球的体积与表面积.
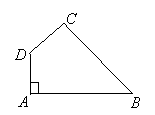 14.如图,在四边形
14.如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求四边形
,求四边形![]() 绕
绕![]() 旋转一周所成几何体的表面积及体积.
旋转一周所成几何体的表面积及体积.
暑假作业五 等差与等比数列
一.填空题
1、已知![]() 为等差数列,
为等差数列,![]() ,
,![]() ,则
,则![]() .
.
2、等差数列中前![]() 项的和为210,其中前四项的和为40,后四项的和为80,则
项的和为210,其中前四项的和为40,后四项的和为80,则![]() 的值等于 ;
的值等于 ;
3、项数为奇数的等差数列,奇数项之和为102,偶数项之和为85,则此数列的中间项为 ;
项数为
4、在数列![]() 在中,
在中,![]() ,
,![]() ,
,![]() ,其中
,其中![]() 为常数,则
为常数,则![]()
5、等差数列![]() 中,
中,![]() ,且
,且![]() ,
,![]() 是数列的前
是数列的前![]() 项和,则
项和,则![]() 取最大值时的
取最大值时的![]() =
=
6、![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,且
项和,且![]() ,则
,则![]()
7、各项都是正数的等比数列![]() 的公比
的公比![]() ,且
,且![]() 成等差数列,则
成等差数列,则![]() 的值是
。
的值是
。
8、等比数列![]() 中,已知
中,已知![]() ,则
,则![]() =
。
=
。
9、若![]() 是等差数列,
是等差数列,![]() 是互不相等的正整数,
是互不相等的正整数,
则有:![]() ,类比上述性质,相应地,对等比数列
,类比上述性质,相应地,对等比数列
![]() ,有 .
,有 .
|
(1)![]() =
;
=
;
(2)若![]() ,则m+n=
。
,则m+n=
。
二、解答题
11、已知数列![]() 的前n项和
的前n项和![]() ,求
,求![]() 的前n项和
的前n项和![]() 。
。
12、已知数列![]() 为等比数列,
为等比数列,![]()
(1)求数列![]() 的通项公式;(2)设
的通项公式;(2)设![]() 是数列
是数列![]() 的前
的前![]() 项和,证明:
项和,证明:![]()
13、设![]() 为等差数列,
为等差数列,![]() 为等比数列,
为等比数列,![]() 分别求出
分别求出![]() 及
及![]() 的前10项和
的前10项和![]() 及
及![]() 。
。
14、已知数列![]() 的首项
的首项![]() ,
,![]() ,
,![]() ….
….
(Ⅰ)证明:数列![]() 是等比数列;(Ⅱ)数列
是等比数列;(Ⅱ)数列![]() 的前
的前![]() 项和
项和![]() .
.
暑假作业六 数列的综合运用
一、填空题
1.若数列![]() 中
中![]() 则
则![]() 的值为 ;
的值为 ;
2.把数列![]() 中各项划分为:(3),(5,7),
(9,11,13) ,
(15,17,19,21)
, (23) , (25,27),(29,31,33) , (35,37,39,41),照此下去,第100个括号里各数的和为
;
中各项划分为:(3),(5,7),
(9,11,13) ,
(15,17,19,21)
, (23) , (25,27),(29,31,33) , (35,37,39,41),照此下去,第100个括号里各数的和为
;
3.已知数列![]() 满足:
满足: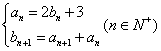 且
且![]() ,则
,则![]() ;
;
4.已知数列![]() 的通项公式为
的通项公式为![]() (n∈N+),则在数列
(n∈N+),则在数列![]() 的前50项中最大项是第
项,最小项是第 项。
的前50项中最大项是第
项,最小项是第 项。
5.计算机信息是按二进制数进行处理的,二进制即“逢二进一”.如 (1101)![]() 表示二进制的数, 将它转换成十进制的形式是
表示二进制的数, 将它转换成十进制的形式是![]() ,那么二进制数()
,那么二进制数()![]() 转换成十进制的形式是 ;
转换成十进制的形式是 ;
6.已知数列![]() 满足
满足![]() ,
,![]() ,则
,则![]() ;
;
7.若![]() 为
为![]() 的各位数字之和,如:
的各位数字之和,如:![]() ,
,![]() ,则
,则![]() ;记
;记
![]() _ ___。
_ ___。
8.在公差为![]() 的等差数列
的等差数列![]() 中,若
中,若![]() 是
是![]() 的前
的前![]() 项和,则数列
项和,则数列![]() 也成等差数列,且公差为
也成等差数列,且公差为![]() ,类比上述结论,相应地在公比为
,类比上述结论,相应地在公比为![]() 的等比数列
的等比数列![]() 中,若
中,若![]() 是数列
是数列![]() 的前
的前![]() 项积,则有
;
项积,则有
;
 9.一次展览会上展出一套由宝石串联制成的工艺品,如图所示.若按照这种规律依次增加一定数量的宝石,则第
9.一次展览会上展出一套由宝石串联制成的工艺品,如图所示.若按照这种规律依次增加一定数量的宝石,则第![]() 件工艺品所用的宝石数为 颗 (结果用
件工艺品所用的宝石数为 颗 (结果用![]() 表示);
表示);
|
|
|
|
10.将自然数按如下规则“放置”在平面直角坐标系中:①每一个自然数“放置”在一个整点(横纵坐标均为整数的点)上;②0在原点,1在![]() ;2在
;2在![]() ;3在
;3在![]() ;4在
;4在![]() ;5
;5![]() 在;6在
在;6在![]() ;······即所有自然数按顺时针“缠绕”在以“
;······即所有自然数按顺时针“缠绕”在以“![]() 的整点坐标为 。
的整点坐标为 。
二、解答题
11.设![]() ,正数数列
,正数数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;(2)若
的通项公式;(2)若![]() 对一切正整数
对一切正整数![]() 都成立,求数列
都成立,求数列![]() 的通项公式。
的通项公式。
12.设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]()
(Ⅰ)求![]() (Ⅱ)证明:
(Ⅱ)证明: ![]() 是等比数列;(Ⅲ)求
是等比数列;(Ⅲ)求![]() 的通项公式
的通项公式
13.在一次人才招聘会上,甲、乙两家公司开出的工资标冷分别是:
甲公司:第一年月工资1500元,以后每年月工资比一年月工资增加230元;
乙公司:第一年月工资2000元,以后每年月工资在一年月工资基础上递增5%.
设某人年初想从甲、乙两公司中选择一家公司去工作。
(1)
若此人分别在甲公司或乙公司连续工作![]() 年,则他在两公司第
年,则他在两公司第![]() 年的月工资分别为多少?
年的月工资分别为多少?
(2) 若此人在一家公司连续工作10年,则从哪家公司得到报酬较多?
14.设数列![]() 满足:若
满足:若![]() ;若
;若![]() .
.
(1)求:![]() ;
;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)证明:![]() .
.
暑假作业七 一元二次不等式及简单线性规划
一.填空题
1、若直线![]() 与曲线
与曲线![]() 恰有一个公共点,则实数
恰有一个公共点,则实数![]() 的取值范围是
。
的取值范围是
。
2、已知实数![]() 、
、![]() 满足
满足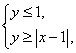 则
则![]() 的最大值是
.
的最大值是
.
3、若![]() ,不等式
,不等式![]() 表示的区域是直线
表示的区域是直线![]() 的
的
4、若不等式<0对一切![]() 恒成立,则实数m的范围为 .
恒成立,则实数m的范围为 .
5、若关于![]() 的不等式
的不等式![]() 有解,则实数a的取值范围是________..
有解,则实数a的取值范围是________..
6、已知不等式![]() 的解集是
的解集是![]() ,则
,则![]() 的解集是 .
的解集是 .
7、设实数![]() 、
、![]() 满足
满足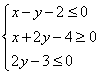 ,则
,则![]() 的最大值是
.
的最大值是
.
8、关于![]() 的方程
的方程![]() ,一个根
,一个根![]() ,另一个根
,另一个根![]() ,则
,则![]() 的范围为
的范围为
9、若实数![]() 时,不等式
时,不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是
10、已知圆![]() 上任一点
上任一点![]()
![]() ,其坐标均使得不等式
,其坐标均使得不等式![]() ≥0恒成立,则实数
≥0恒成立,则实数![]() 的取值范围是 .
的取值范围是 .
11、解关于![]() 的不等式
的不等式
(1)![]() (2)
(2)![]() (3)
(3) ![]()
12、(1)画出不等式组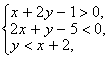 所表示的平面区域.
所表示的平面区域.
(2)试求由不等式![]() 及
及![]() 所表示的平面区域的面积.
所表示的平面区域的面积.
13、已知变量x、y满足下列不等式组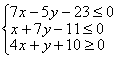 ,
,
(1)
求![]() 的最大值和最小值;(2)求
的最大值和最小值;(2)求![]() 的最大值和最小值。
的最大值和最小值。
14、某工厂生产甲、乙两种产品,已知生产1t甲产品需用A种原料2t、B种原料6t;生产1t乙产品需用A种原料5t、B种原料3t。又知每t甲产品价值4万元,每t乙产品价值3万元。但生产这两种产品所消耗原料A不能超过10t,消耗原料B不能超过18t,求甲、乙两种产品各生产多少t时,创造的产值最高。
暑假作业八 基本不等式及应用
一.填空题
1、函数![]() 的最大值是
.
的最大值是
.
2、已知![]() ,且
,且![]() ,则
,则![]() 的最小值是____________
的最小值是____________
3、已知![]() 且
且![]() ,则
,则![]() 的最小值为 ;
的最小值为 ;
4、已知函数![]() ,则此函数的最小值为
,则此函数的最小值为
5、已知函数![]() ,则此函数的最小值为 ;
,则此函数的最小值为 ;
6、若正数![]() 满足
满足![]() ,则
,则 ![]() 的取值范围是
的取值范围是
7、已知![]() 且
且![]() ,则
,则![]() 的最小值为
的最小值为
8、若函数![]() (
(![]() )在
)在![]() 上的最大值为
上的最大值为![]() ,则
,则![]() 的值为 .
的值为 .
9、下列函数值最小值为4的是
(1) ![]() (2)
(2)
![]()
(3) ![]() (4)
(4)![]()
10、函数![]() 的最大值为 。
的最大值为 。
二.解答题
11、(1)若![]() 且满足
且满足![]() ,求
,求![]() 的最小值;
的最小值;
(2)设![]() ,试比较
,试比较![]() 的大小。
的大小。
12、已知![]() ,(1)求
,(1)求![]() 的最小值;(2)求
的最小值;(2)求![]() 的最小值。
的最小值。
13、某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(1)求该企业使用该设备![]() 年的年平均污水处理费用
年的年平均污水处理费用![]() (万元);
(万元);
(2)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
14、(1)已知![]() 为非零向量根据平面向量数量积的定义证明向量性质:
为非零向量根据平面向量数量积的定义证明向量性质:![]() ,并用该性质证明不等式:
,并用该性质证明不等式:![]() 。
。
(2)探求函数![]() 的最大值与最小值。如有最大值与最小值,一并求出何时取到最大值与最小值。
的最大值与最小值。如有最大值与最小值,一并求出何时取到最大值与最小值。
暑假作业九 任意角的三角函数
一、填空题
1.已知![]() ,那么角
,那么角![]() 是第 象限角.
是第 象限角.
2.![]() 的值为 .
的值为 .
3.若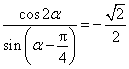 ,则
,则![]() 的值为
.
的值为
.
4.已知![]() ,则
,则![]() 的值为
.
的值为
.
5.若角α终边在直线![]() .
.
6.在(0,2![]() )内,使
)内,使![]() 成立的
成立的![]() 的取值范围是
.
的取值范围是
.
7.α在第二象限,2α在第_______象限,则![]() 在第_______象限,
在第_______象限,![]() 在第________象限.
在第________象限.
8. 已知![]() (其中
(其中![]() 、
、![]() 为常数且
为常数且![]() ),如果
),如果![]() ,则
,则![]() 的值为
。.
的值为
。.
9. 如果![]() ,那么
,那么![]() 的值等于
。
的值等于
。
10. 若![]() ,
,![]() ,则
,则![]() 角的终边在第
象限。
角的终边在第
象限。
二、解答题
11.若![]() 的值.
的值.
12.(1)扇形的中心角为120°,则此扇形的面积与其内切圆的面积之比为?
(2)已知一扇形的周长是
13.已知![]() 的取值范围.
的取值范围.
14.若θ是第二象限,那么![]() 的值所对应的符号是什么?
的值所对应的符号是什么?
暑假作业十 三角函数的图像与性质
一、填空题
1.函数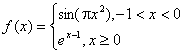 ,若
,若![]() ,则
,则![]() 的所有可能值为
的所有可能值为
2.函数![]() 的最小正周期是
的最小正周期是
3.为了得到函数![]() 的图象,可以将函数
的图象,可以将函数![]() 的图象
.
的图象
.
4.若![]() 对任意
对任意![]() 恒成立,则实数
恒成立,则实数![]() 的范围为 .
的范围为 .
5.数![]() 的值域为
.
的值域为
.
6.函数![]() 在
在![]() 上的最大值为
上的最大值为
7.若![]() ,
,![]() ,则
,则![]() 的取值范围是
。
的取值范围是
。
8. 函数![]() 的单调区间为
。
的单调区间为
。
9. 已知![]() ,恒有
,恒有![]() 成立,且
成立,且![]() ,则实数m的值为
,则实数m的值为
10. 关于函数f(x)=2sin(3x-![]() ),有下命题:
),有下命题:
(1)其最小正周期是![]() ;(2)其图象可由y=2sin3x向左平移
;(2)其图象可由y=2sin3x向左平移![]() 个单位得到;(3)其表达式可改写为y=2cos(3x-
个单位得到;(3)其表达式可改写为y=2cos(3x-![]() ); (4)在x∈[
); (4)在x∈[![]() ]上为增函数。其中正确的命题的序号为_____________
]上为增函数。其中正确的命题的序号为_____________
二、解答题
11.已知![]() 是三角形
是三角形![]() 三内角,向量
三内角,向量![]() ,且
,且![]()
(Ⅰ)求角![]() ;
;
(Ⅱ)若![]() ,求
,求![]()
12.将一块圆心角为1200,半径为
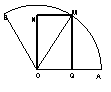

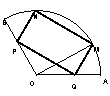

13.是否存在实数a,使得函数![]() 在闭区间
在闭区间![]() 上的最大值是1?若存在,求出对应的a值,若不存在,试说明理由。
上的最大值是1?若存在,求出对应的a值,若不存在,试说明理由。
14.设函数![]()
(I)写出函数![]() 的最小正周期T及单调递增区间;
的最小正周期T及单调递增区间;
(II)若x∈[![]() ]时,函数
]时,函数![]() 的最小值为2,求此时函数
的最小值为2,求此时函数![]() 的最大值,并指出x取何值时
的最大值,并指出x取何值时![]() 取得最大值。
取得最大值。
暑假作业十一 两角和与差的三角函数
一、填空题
1. ![]() = ;
= ;
2.![]() =
;
=
;
3.![]() ;
;
4.![]() 则
则![]() ;
;
5.若f(sinx)=3-cos2x,则f ( cosx)= ;
6.![]() 则
则![]() ;
;
7.已知![]() 且
且![]() ,则
,则![]() 的值为
;
的值为
;
8.![]()
![]() ;
;
9.已知![]() 则
则![]() ;
;
10.在△ABC中,![]() 则
则![]() 的取值范围是 ;
的取值范围是 ;
二、解答题
11. 已知![]() 、
、![]() 均为锐角,
均为锐角,![]() 求:
求:![]() 。
。
12..已知![]() 是方程
是方程![]() 的两根,求下列各式的值:
的两根,求下列各式的值:
(1)![]() (2)
(2)![]() (3)
(3)![]()
13.已知![]()
![]() ,sin(
,sin(![]() )=-
)=-![]() sin
sin![]() 求cos
求cos![]()
14.已知![]() ,求
,求![]() 的值
的值
暑假作业十二 正弦定理和余弦定理
一、填空题
1.在△ABC中,已知A=![]() ,
,![]() 则△ABC的面积等于 ;
则△ABC的面积等于 ;
2.在△ABC中,若![]() 则△ABC的形状是
三角形;
则△ABC的形状是
三角形;
3.在△ABC中.![]() ,
,![]() 则
则![]() ;
;
4.在△ABC中,![]() 则△ABC的形状是 三角形;
则△ABC的形状是 三角形;
5.(08湖南)在![]() 中,AB=3,AC=2,BC=
中,AB=3,AC=2,BC=![]() ,则
,则![]() ;
;
6.(08江苏)若![]() ,则
,则![]() 的最大值是
的最大值是
7.在三角形ABC中,![]() 的值为
;
的值为
;
8.在△ABC中,若有A>B,则下列不等式中
① sinA>sinB; ② cosA<cosB; ③ sin
你认为正确的序号为 ;
9.在![]() ,则塔高为 ;
,则塔高为 ;
10.在△ABC中,内角A、B、C所对的边分别为a、b、c,给出下列结论:
①若A>B>C,则![]() ;
;
②若![]() ;
;
③必存在A、B、C,使![]() 成立;
成立;
④若![]() ,则△ABC必有两解.
,则△ABC必有两解.
其中,真命题的编号为 .(写出所有真命题的编号)
二、解答题
11.(宁夏)
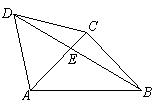 如图,
如图,![]() 是等边三角形,
是等边三角形,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() .
.
12.在△ABC中,A=![]() ,b=1,
,b=1, ![]()
![]() ,求
,求![]() 的值。
的值。
13. 在![]() 中,内角
中,内角![]() 对边的边长分别是
对边的边长分别是![]() ,已知
,已知![]() ,
,![]() .
.
(Ⅰ)若![]() 的面积等于
的面积等于![]() ,求
,求![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 的面积。
的面积。
14.在长江某流口处,江水以![]() 的速度向东流,一渡船在江南岸的A码头,预定要在
的速度向东流,一渡船在江南岸的A码头,预定要在![]() 后到达北岸B码头。见图设
后到达北岸B码头。见图设![]() 为正北方向,已知B码头在A码头的北偏东
为正北方向,已知B码头在A码头的北偏东![]() ,并与A码头相距
,并与A码头相距![]() .该渡船应按什么方向航行?速度是多少(角度精确到
.该渡船应按什么方向航行?速度是多少(角度精确到![]() ,速度精确到
,速度精确到![]()
 |
暑假作业十三 平面向量的基本概念及表示
1.在直角坐标系中,已知![]() ,那么点A构成的图形是
( )
,那么点A构成的图形是
( )
A.一个点 B.一条直线 C. 一个圆 D.不能确定
2.下列说法错误的是 ( )
A.零向量没有方向
B.零向量长度为
C.零向量与任一向量平行 D.零向量的方向任意
3. 下列说法中不正确的是 ( )
A.若![]() ,则
,则![]()
B.若![]() ,则
,则![]() 所在直线平行或重合
所在直线平行或重合
C.若![]() 同向,则
同向,则![]()
D.若![]() ,则
,则![]() 所在直线重合
所在直线重合
4. 设![]() ,则
,则![]() 等于
( )
等于
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5. 在四边形![]() 中,
中,![]() ,且
,且![]() ,则四边形是
,则四边形是
6. 若![]() ,且非零向量
,且非零向量![]() 不平行,则
不平行,则![]() 与
与![]() 所在直线所成的角是
所在直线所成的角是
7. 已知![]() ,
,![]() 与
与![]() 相等,则
相等,则![]()
8.若向量![]() 共线且方向相反,则
共线且方向相反,则![]() =
=
9. 若![]() 和
和![]() 是平面内所有向量的一组基底,且
是平面内所有向量的一组基底,且![]() 不能作为一组基底,则
不能作为一组基底,则![]() 的值
的值
为
10.已知![]() ,则线段AB中点坐标为
,则线段AB中点坐标为
11.已知向量![]() 的模
的模![]() 求
求![]() 的最大值和最小值。
的最大值和最小值。
12.如图所示,OA、DB是以向量![]() ,
,![]() 为边的平行四边形。又
为边的平行四边形。又![]() ,
,![]() ,试用
,试用![]() ,
,![]() 表示
表示![]() ,
,![]() ,
,![]() 。
。
13.设![]() ,其中
,其中![]() 、
、![]() 为两个不共线的向量,
为两个不共线的向量,
求证:![]() 三点共线。
三点共线。
14. 已知点![]() 及
及![]() ,求:
,求:
(1)若点P在第二象限,求![]() 的取值范围;
的取值范围;
(2)四边形OABP能否成为平行四边形?若能,求出相应的![]() 值;若不能,请说明理由.
值;若不能,请说明理由.
暑假作业十四 平面向量的数量积及应用
1.与向量![]() 垂直的单位向量为 ( )
垂直的单位向量为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() 或
或![]() (D)
(D)![]() 或
或![]()
2.已知![]() ,若
,若![]() 与
与![]() 的夹角为钝角,则
的夹角为钝角,则![]() 的取值范围是 ( )
的取值范围是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.在![]() 中,
中,![]() ,且
,且![]() ,则
,则![]() 是
( )
是
( )
(A)锐角三角形 (B)直角三角形 (C)钝角三角形 (D)等腰三角形
4.下面给出的几个有关向量的关系式:①![]() ②
②![]() ③
③ ![]() ④
④![]() ,
,
其中正确的关系式有 (填序号)
5.正三角形ABC的边长为2,则![]() = .
= .
6.已知![]() ,并且
,并且![]() ,则
,则![]() =
.
=
.
7.已知向量![]() 不超过5,则k的取值范围是
不超过5,则k的取值范围是
8.直角坐标平面![]() 中,若定点
中,若定点![]() 与动点
与动点![]() 满足
满足![]() ,则点P的轨迹
,则点P的轨迹
方程是
9. 已知点![]()
![]() ,
,![]()
![]() ,点
,点![]() 在
在![]()
![]() 的延长线上,且
的延长线上,且![]()
![]() =3
=3![]()
![]() ,
,
则点![]() 的坐标为_____________
的坐标为_____________
10. 已知向量![]() ,
,![]() 不共线,若
不共线,若![]() =
=![]() +
+![]() ,
,![]() =3
=3![]() -
-![]() ,
,![]() =
=![]()
![]() -5
-5![]() ,
,
且![]() ,
,![]() ,
,![]() 三点共线,则
三点共线,则![]() =_________
=_________
12.已知![]() 与
与![]() 是非零向量,且
是非零向量,且![]() ,
,![]() ,求:
,求:![]() 与
与![]() 的夹角.
的夹角.
13.已知![]() 与
与![]() 之间有关系
之间有关系![]() ,其中
,其中![]() ,(1)用
,(1)用![]() 表示
表示![]() ;(2)求
;(2)求![]() 的最小值,并求此时
的最小值,并求此时![]() 与
与![]() 的夹角的大小。
的夹角的大小。
14. 已知![]() ,
,![]() (
(![]() 为常数)
为常数)
(1)求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)若![]() ,方程
,方程![]() =0有唯一解,求实数a的取值范围.
=0有唯一解,求实数a的取值范围.
暑假作业十五 集合的概念和运算
一.填空题:
1.设集合![]() ,
,![]() ,那么M,m关系是
,那么M,m关系是
2.下面六个关系式中正确的序号是
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;⑥
;⑥![]()
3.若![]() ,则
,则![]()
4.已知![]() ,则
,则![]() 的关系应该是
的关系应该是
5.集合![]() ,则
,则![]() .
.
6.设全集![]() ,则
,则![]() .
.
7. ![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的取值范围是__
.
的取值范围是__
.
8.已知集合![]() 中只有一个元素,则实数
中只有一个元素,则实数![]() 的取值集合为
.
的取值集合为
.
9. 对于集合N={1, 2, 3,…, n}及其它的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数。例如集合{1, 2, 4, 6, 9}的交替和是9–6+4–2+1=6,集合{5}的交替和为5。当集合N中的n=2时,集合N={1, 2}的所有非空子集为{1},{2},{1, 2},则它的“交替和”的总和S2=1+2+(2–1)=4,请你尝试对n=3、n=4的情况,计算它的“交替和”的总和S3、S4,并根据其结果猜测集合N={1, 2, 3,…, n}的每一个非空子集的“交替和”的总和Sn= .
10. 对于任意的两个实数对(a,b)和(c,d),规定当且仅当a=c, b=d时(a, b)=(c,d);现定义两种运算,运算“![]() ”为:(a,b)
”为:(a,b)![]() (c,d)=(ac-bd,bc+ad);运算“
(c,d)=(ac-bd,bc+ad);运算“![]() ”为:(a,b)
”为:(a,b)![]() (c,d)=(a+c,b+d).设p、q
(c,d)=(a+c,b+d).设p、q![]() R.若(1,2)
R.若(1,2)![]() (p、q)=(5,0).则(1,2)
(p、q)=(5,0).则(1,2)![]() (p,q)等于
.
(p,q)等于
.
二.解答题
12. 若集合![]() .
.
(1)若![]() ,求实数
,求实数![]() 的取值集合;(2)若
的取值集合;(2)若![]() ,求实数
,求实数![]() 的取值集合;
的取值集合;
(3)若![]() ,求实数
,求实数![]() 的取值集合.
的取值集合.
13. 设关于![]() 的不等式
的不等式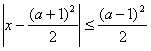 的解集为A,x2-3(
的解集为A,x2-3(![]() +1)x+2(3
+1)x+2(3![]() +1)≤0的解集为B,求使
+1)≤0的解集为B,求使![]() 的
的![]() 的取值范围.
的取值范围.
14.![]() ,其中
,其中![]() ,由
,由![]() 中的元素构成两个相应的集合:
中的元素构成两个相应的集合:
![]() ,
,![]() .其中
.其中![]() 是有序数对,集合
是有序数对,集合![]() 和
和![]() 中的元素个数分别为
中的元素个数分别为![]() 和
和![]() .若对于任意的
.若对于任意的![]() ,总有
,总有![]() ,则称集合
,则称集合![]() 具有性质
具有性质![]() .
.
(I)对任何具有性质![]() 的集合
的集合![]() ,证明:
,证明:![]() ;
;
(II)判断![]() 和
和![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
.
暑假作业十六 函数的图象和性质
一.填空题:
1.设![]() ,则
,则![]() 的值为
的值为
2.方程![]() 的根
的根![]() ,
,![]() ∈Z,则
∈Z,则![]() =
=
3.函数![]() 的图象是由
的图象是由![]() 的图象经过
变换得到的.
的图象经过
变换得到的.
4.设偶函数![]() 的定义域为R,当
的定义域为R,当![]() 时,
时,![]() 是增函数,则
是增函数,则![]() ,
,![]() ,
,![]() 的大小关系是
的大小关系是
5.若![]() 对任意的正实数x成立,则
对任意的正实数x成立,则![]()
![]()
![]() .
.
6.函数![]() 在
在![]() 上是减函数,则
上是减函数,则![]() 的取值范围是
.
的取值范围是
.
7.设函数![]() 是奇函数且周期为3,
是奇函数且周期为3,![]() = .
= .
8.![]() 是定义在R上的以3为周期的偶函数,且
是定义在R上的以3为周期的偶函数,且![]() ,则方程
,则方程![]() =0在区间(0,6)内解的个数的最小值是
。
=0在区间(0,6)内解的个数的最小值是
。
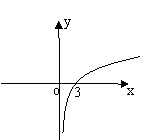 9.已知
9.已知![]() 是定义域为
是定义域为![]() 的奇函数,在区间
的奇函数,在区间![]() 上单调递增,当
上单调递增,当![]() 时,
时,![]() 的图像如右图所示:
的图像如右图所示:
若![]() ,则
,则![]() 的取值范围是
;
的取值范围是
;
10.给出下列四个结论:
①函数![]() (
(![]() 且
且![]() )与函数
)与函数![]() (
(![]() 且
且![]() )的定义域相同;
)的定义域相同;
②函数![]() (
(![]() 为常数)的图像可由函数
为常数)的图像可由函数![]() 的图像经过平移得到;
的图像经过平移得到;
③函数![]() (
(![]() )是奇函数且函数
)是奇函数且函数![]() (
(![]() )是偶函数;
)是偶函数;
④函数![]() 是周期函数.其中正确结论的序号是___________________.(填写你认为正确的所有结论序号)
是周期函数.其中正确结论的序号是___________________.(填写你认为正确的所有结论序号)
二、解答题:
11.若光线通过一块玻璃,其强度要损失![]() .把几块这样的玻璃重叠起来,设光线原来的强度为
.把几块这样的玻璃重叠起来,设光线原来的强度为![]() ,通过
,通过![]() 块玻璃后强度为
块玻璃后强度为![]() .
.
(1)写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)至少通过多少块玻璃后,光线强度减弱到原来的![]() 以下?(
以下?(![]() )
)
12.已知函数![]() .(1)用分数函数的形式表示该函数;(2)画出该函数的图象;(3)写出该函数的定义域、值域、奇偶性、单调区间.
.(1)用分数函数的形式表示该函数;(2)画出该函数的图象;(3)写出该函数的定义域、值域、奇偶性、单调区间.
13.已知函数![]()
![]() 是奇函数.
是奇函数.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 在
在![]() 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ,求实数
,求实数![]() 与
与![]() 的值.
的值.
14.已知定义域在[0,1]的函数f(x)同时满足:(1)对于任意![]() 总有
总有![]() (2)f(1)=1
(2)f(1)=1
(3)若![]() 则有
则有![]()
①试求f(0)的值 ②判断函数f(x)的单调性并求函数f(x)的最大值。
暑假作业十七 幂、指、对函数
一、填空题
1.函数![]() 且
且![]() )的图象恒过定点
.
)的图象恒过定点
.
2.已知函数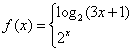
![]() ,则
,则![]() 的值是
.
的值是
.
3.函数![]() 的定义域是
.
的定义域是
.
4.已知函数![]() 的定义域是
的定义域是![]() ,则函数
,则函数![]() 的定义域是
.
的定义域是
.
5.要使函数![]() 的图象不经过第二象限,则
的图象不经过第二象限,则![]() 的取值范围是 .
的取值范围是 .
6.函数![]() 在
在![]() 中最大值比最小值大
中最大值比最小值大![]() ,则
,则![]() 的值为__________
的值为__________
7.已知函数![]() 在
在![]() 上是减函数,则
上是减函数,则![]() 的取值范围为
.
的取值范围为
.
8.关于![]() 方程
方程![]() 有负根,则实数
有负根,则实数![]() 取值范围是_________.
取值范围是_________.
二、解答题
9.若关于![]() 的方程
的方程![]() 有实根,试求实数
有实根,试求实数![]() 的取值范围.
的取值范围.
10.已知函数![]() 是幂函数,且过点
是幂函数,且过点![]() .
.
(1)求函数![]() 的解析式;(2)判断函数
的解析式;(2)判断函数![]() 的奇偶性;
的奇偶性;
(3)判断函数![]() 的单调性,并作出函数
的单调性,并作出函数![]() 的图象.
的图象.
11.设![]() ,若当
,若当![]() 时
时![]() 有意义,求实数
有意义,求实数![]() 取值范围.
取值范围.
12.已知函数![]() ,
,
(1)求函数![]() 的定义域和值域;(2)讨论函数
的定义域和值域;(2)讨论函数![]() 的奇偶性;(3)讨论函数
的奇偶性;(3)讨论函数![]() 的单调性.
的单调性.
13.对于函数![]() ,解答下述问题:
,解答下述问题:
(1)若函数的定义域为R,求实数![]() 的取值范围;
的取值范围;
(2)若函数的值域为R,求实数![]() 的取值范围;
的取值范围;
(3)若函数在![]() 内有意义,求实数
内有意义,求实数![]() 的取值范围;
的取值范围;
(4)若函数的定义域为![]() ,求实数
,求实数![]() 的值;
的值;
(5)若函数的值域为![]() ,求实数
,求实数![]() 的值;
的值;
(6)若函数在![]() 内为增函数,求实数
内为增函数,求实数![]() 的取值范围.
的取值范围.
暑假作业十八 函数模型和应用
一、填空题
1.若![]() ,
,![]() ,则函数
,则函数![]() 的图象不经过第 象限;
的图象不经过第 象限;
2.某药品零售价![]() 年比
年比![]() 年上涨
年上涨![]() ,现要求
,现要求![]() 年比
年比![]() 年只上涨
年只上涨![]() ,则
,则![]() 年比
年比![]() 年应降价 % ;
年应降价 % ;
3.一种放射性物质不断变化为其他物质,每经过一年剩留的质量约是原来的84%,估计约经过x年,该物质的剩留量是原来的一半?则列出解题的关键等式 ;
4.如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联.连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点![]() 向结点
向结点![]() 传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为 ;
传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为 ;
5.如图,是一个树形图的生长过程,依据图中所示的生长规律,第8行的实心圆点的个数是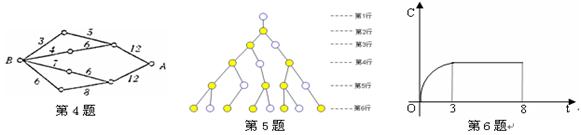 ;
;
6.某工厂八年来某种产品的总产量![]() 与时间
与时间![]() (年)的函数关系如图所示,下列四说法:
(年)的函数关系如图所示,下列四说法:
①前三年中产量增长速度越来越快;②前三年中产量增长速度越来越慢;
③第三年后,这种产品停止生产;④第三年后,年产量保持不变.其中正确的是
 7.如图所示,动物园要建造一面靠墙的2间面积相同的矩形熊猫居室,如果可供建造围墙的材料总长是
7.如图所示,动物园要建造一面靠墙的2间面积相同的矩形熊猫居室,如果可供建造围墙的材料总长是![]() = 才能使所建造的每间熊猫居室面积最大,每间熊猫居室的最大面积是 ;
= 才能使所建造的每间熊猫居室面积最大,每间熊猫居室的最大面积是 ;
8.如图所示,液体从一圆锥形漏斗注入一圆柱形桶中,开始时漏斗盛满液体,经过3分钟注完.已知圆柱中液面上升的速度是一个常数,![]() 是圆锥形漏斗中液面下落的距离,则
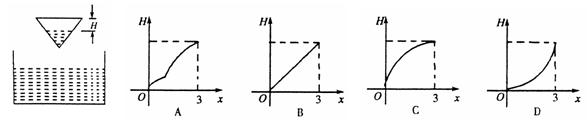
是圆锥形漏斗中液面下落的距离,则![]() 与下降时间
与下降时间![]() (分钟)的函数关系用图象表示只可能是----------------------------------------- ( )
(分钟)的函数关系用图象表示只可能是----------------------------------------- ( )
9.某种计算机病毒是通过电子邮件进行传播的,如果某台计算机感染上这种病毒,那么它就会在下一轮病毒发作时传播一次病毒,并感染其他20台末感染病毒的计算机,现有10台计算机被第1轮病毒感染,设第n轮病毒感染的计算机台数f(n),则f(2)= ;
f(n)、f(n+1)、f(n-1)之间的等量关系是: ;
10.在测量某物理量的过程中,因仪器和观察的误差,使得几次测量分别得到![]() ,共
,共![]() 个数据,我们规定所测量物理量的“最佳近似值
个数据,我们规定所测量物理量的“最佳近似值![]() ”这样一个量,与其他的近似值比较,
”这样一个量,与其他的近似值比较,![]() 与各数据的差的平方和最小,依此规定,从
与各数据的差的平方和最小,依此规定,从![]() ,推出
,推出![]() _______________.
_______________.
二、解答题
11.用动力船拖动载重量相等的小船若干只,在两个港口之间来回运货.如果一只动力船拖![]() 只小船,则每天能往返
只小船,则每天能往返![]() 次;如果一只动力船拖
次;如果一只动力船拖![]() 只小船,则每天能往返
只小船,则每天能往返![]() 次.已知小船只数的增多会按比例地减少往返的次数,试求每只动力船拖多少只小船,每天往返多少次,能使运货总量最大?
次.已知小船只数的增多会按比例地减少往返的次数,试求每只动力船拖多少只小船,每天往返多少次,能使运货总量最大?
12.某商场对顾客实行购物优惠活动,规定一次购物付款总额:(1)如果不超过200元,则不予优惠;(2)如果超过200元但不超过500元,则按标价给予9折优惠;(3)如果超过500元,其500元按(2)条给予优惠,超过500元的部分给予7折优惠.某人两次去购物,分别付款168元和423元,假设他把这些商品一次性买来,则应付款 元.
13.某公司为了实现![]() 万元利润目标,准备制定一个激励销售部门的奖励方案:在销售利润达到
万元利润目标,准备制定一个激励销售部门的奖励方案:在销售利润达到![]() 万元时,开始按销售利润进行奖励,且奖金
万元时,开始按销售利润进行奖励,且奖金![]() 万元随销售利润
万元随销售利润![]() 万元的增加而增加,但奖金总数不得超过
万元的增加而增加,但奖金总数不得超过![]() 万元,同时奖金不超过利润的
万元,同时奖金不超过利润的![]() ,现有三个奖励模型
,现有三个奖励模型![]() 、
、![]() 、
、![]() ,试问:三种模型中是否存在符合公司要求的模型?
,试问:三种模型中是否存在符合公司要求的模型?
14.某工厂统计资料显示,该厂生产的某种产品的次品率![]() 与日产量
与日产量![]() (千克)(
(千克)(![]() 且
且![]() )的关系如下表
)的关系如下表

且已知每生产![]() 元,每生产
元,每生产![]() 元(
元(![]() )
)
(1)写出该厂生产该产品的日赢利额![]() (元)关于日产量
(元)关于日产量![]() 的一个函数关系式;
的一个函数关系式;
(2)为了获得最大赢利,该厂生产该产品的日产量应定为多少千克?
高一暑假作业参考答案
暑假作业一参考答案
1.2x-y+6=0; 2.3; 3.x+y+3=0; 4.![]() ; 5.三; 6.(
; 5.三; 6.(![]() ); 7.2x-3y-4=0
); 7.2x-3y-4=0
8.3; 9.2x+y-4=0; 10.![]() ; 11.103x+43y=0;
; 11.103x+43y=0;
12.(1)3x+y=0,x+y+2=0(2)![]() ; 13.(1)-2,2(2)
; 13.(1)-2,2(2)![]()
![]()
14.1(1)x+y-3=0(2)x+2y-4=0;2(2,3)
暑假作业二参考答案
1.![]() ;2. x+y-1=0; 3.
;2. x+y-1=0; 3.![]() ;4.
;4.![]() ;5.
;5.![]() ;
;
6.![]() 或
或![]() ;7.
;7.![]() ;8.
;8.![]() ;9.-2;10. x=0或y=- x+3;
;9.-2;10. x=0或y=- x+3;
11.![]() ;12.略;13.(1)
;12.略;13.(1) ![]() ;14.(1)
;14.(1)![]() (2)不能;
(2)不能;
暑假作业三参考答案
1.![]() 或
或![]() ; 2.
; 2.![]() ; 3.异面或相交; 4.平行; 5.②③;
; 3.异面或相交; 4.平行; 5.②③;
6.![]() ; 7.
; 7.![]() ; 8.
; 8.![]() ; 9.2; 10. ③④; 11.三点共线;
; 9.2; 10. ③④; 11.三点共线;
![]()
![]() 13.证明 (1)∵ AA1⊥平面A1B
13.证明 (1)∵ AA1⊥平面A1B
∴平面AA1B1B⊥平面A1B![]() 平面A1B
平面A1B
又△ABC中,AC=BC,∴△A1B
∵M是A1B1的中点,∴C
(2)由(1)知,AM是AC1在平面AA1B1B内的射影.
∵AC1⊥A1B,根据三垂线定理的逆定理知, A1B⊥AM.
(3)由(1)(2)知,A1B⊥平面AMC1.
同理, A1B⊥平面NB
14.(1)连结![]() 与
与![]() 相交于点
相交于点![]() ,再连结
,再连结![]() ,则易证
,则易证![]() 为
为![]() 的中点,由三角形中位线定理知,
的中点,由三角形中位线定理知,
![]() ,从而证得BG//平面
,从而证得BG//平面![]()
(2)连结![]() 与
与![]() 相交于点
相交于点![]() ,再连结
,再连结![]() 及
及![]() ,则
,则![]() 即可.
即可.
设正方体棱长为![]() ,则
,则![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
即![]() 时,平面
时,平面![]() 平面
平面![]() .
.
暑假作业四参考答案
1.平行投影的投影线互相平行,而中心投影的投影线相交于一点;2.![]() ;
;
3.![]() 或
或![]() ;4.
;4. ![]() ;5.
;5.![]() ;6.
;6.![]() ;7. A、M与D. 8.
;7. A、M与D. 8.![]()
9.圆锥的母线长为![]() cm.10.
cm.10.![]() 11.
11.![]() 12.
12. ⑴
⑴
⑵![]()
13.![]()
14.解:![]()
![]()
![]()
![]()
![]()
![]()
暑假作业五部分答案
9. ![]() ;10.
;10. ![]() ,11
,11
暑假作业六参考答案
1.-1; 2.1992;3.![]() ;4.11,10;5.
;4.11,10;5.![]() ;6.
;6. ;
;
7.5;8. ![]() ;9.
;9.![]() ;10.
;10.![]() ;
;
11.解:(1)由![]() ,
,![]() ,
,![]()
得![]()
![]() ①
①
![]() ,
②
,
②
即 ![]() ,
,
即 ![]() ,
,
即 ![]()
∵![]() >
>![]() ,∴
,∴![]() ,即数列
,即数列![]() 是公差为2的等差数列,
是公差为2的等差数列,
由①得,![]() ,解得
,解得![]() ,
,
因此 ,数列![]() 的通项公式为
的通项公式为![]() .
.
(2)![]() ③
③
当![]() 时,有
时,有![]() ④
④
③-④,得 ![]() ,
,
由![]() 得,
得,![]()
12.(Ⅰ)因为![]() ,所以
,所以![]()
由![]() 知
知
![]()
![]()
得![]() ①
①
所以![]()
![]()
![]()
(Ⅱ)由题设和①式知
![]()
![]()
![]()
所以![]() 是首项为2,公比为2的等比数列。
是首项为2,公比为2的等比数列。
(Ⅲ)![]()
![]()
13. 由题意得:甲公司的各年的月工资成以1500为首项,以230为公差为的等差数列。
![]()
而10年的总工资为![]()
乙公司和各年的月年工资以2000为首项,以1.05为公比的等比数列。
![]()
同样的10年和总工资为![]() ,
,
![]()
所以在甲公司获得的报酬比较多。
14. (1)22
作业7答案:
1、![]() 2、4;3、下方;4、
2、4;3、下方;4、![]() ;5、
;5、![]() ;6、(-1,2);7、
;6、(-1,2);7、![]() ;8、
;8、![]() ;9、
;9、![]() ;10、
;10、![]() :11、(1)
:11、(1)![]() (2)
(2)![]() (3)
(3)![]() ;
;
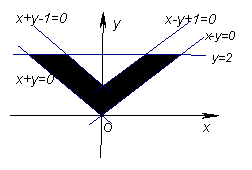
12、解:(1)如图所示,其中的阴影部分便是欲表示的平面区域.
 (2)可将原不等式组分解成如下两个不等式组:①
(2)可将原不等式组分解成如下两个不等式组:①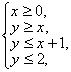 或②
或②
上述两个不等式组所表示的平面区域为如图所示,其形状如一展翅的海鸥.它所围成的面积为![]()
13、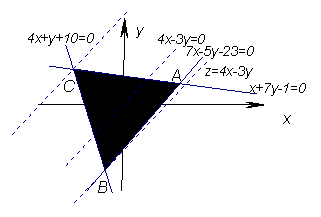 解:不等式组
解:不等式组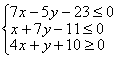 所表示的平面区域如图所示的
所表示的平面区域如图所示的![]() 的内部(包括边界),其中A,B,C三点的坐标分别为
的内部(包括边界),其中A,B,C三点的坐标分别为![]() 。
。
(1)作一组与直线![]() 平行的直线
平行的直线![]() ,从图不难看出,当直线过点B时z值最大,且
,从图不难看出,当直线过点B时z值最大,且![]() ;当直线过点C时z值最小,且
;当直线过点C时z值最小,且![]() 。
。
(2)由![]() 得
得![]() ,它表示点P(x,y)到原点(0,0)的距离,结合
,它表示点P(x,y)到原点(0,0)的距离,结合![]() 区域,易得点B到原点的距离最大。
区域,易得点B到原点的距离最大。![]() ;而到原点的距离最小,
;而到原点的距离最小,![]() 。综上所述,(1)
。综上所述,(1)![]() 的最大值为14,最小值为
的最大值为14,最小值为![]() ;(2)
;(2)![]() 的最大值为37,最小值为0。
的最大值为37,最小值为0。
14、解:将已知数据列成下表
| 产品 资源 | 甲产品 (1t) | 乙产品 (1t) | 资源限额 (t) |
| A原料t | 2 | 5 | 10 |
| B原料t | 6 | 3 | 18 |
| 产值(万元) | 4 | 3 |
 设生产甲种产品为x t,乙种产品为y t,产值为z万元,那么,有约束条件
设生产甲种产品为x t,乙种产品为y t,产值为z万元,那么,有约束条件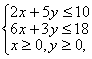 ,则
,则![]() 。
。
由不等式组作出可行域如图,这里
![]() ,
,
由方程组![]() 解得交点
解得交点![]() 。
。
当直线![]() 过A点时,有
过A点时,有
![]() (万元)。
(万元)。
所以生产甲种产品![]() t,乙种产品1
t,乙种产品1![]() 时,产值为13万元最高。
时,产值为13万元最高。
作业8答案:
1、![]() ;2、
;2、![]() ;3、16;4、6;5、
;3、16;4、6;5、![]() ;6、
;6、![]() ; 7、
; 7、![]() ;8、
;8、![]() ;9、(3)
;9、(3)
10、![]() ;
;
11、解:(1)∵![]() ,设
,设![]() ,则有
,则有![]() ,即
,即![]()
∴![]() 或
或![]() 。
。
(2)∵![]() ,∴
,∴![]() 。;
。;
12、解:(1)∵![]() ,∴
,∴![]()
(2)![]() ;
;
13、(1)![]() ;(2)10年;
;(2)10年;
14、(1)![]() 为非零平面向量的数量积的定义:
为非零平面向量的数量积的定义:![]() ,其中
,其中![]() 为两向量的夹角。
为两向量的夹角。
∴![]() 即
即![]() …… 3分
…… 3分
设![]() 则
则![]()
![]()
由![]() 性质,得
性质,得![]() …… 6分
…… 6分
(2)法一:设![]() (O为坐标原点),则
(O为坐标原点),则![]()
所以![]()
![]()
![]() …… 8分
…… 8分
因为![]() ,所以向量
,所以向量![]() 的终点
的终点![]() 在以原点为圆心 ,2为半径的圆在
在以原点为圆心 ,2为半径的圆在
第一象限的圆弧上。 …… 10分
当O,A,B三点共线时,![]() 取到最大值为1,所以
取到最大值为1,所以![]() 当
当![]() 时,
时,![]() 达到最大,
达到最大,![]() 取到最小值,所以
取到最小值,所以![]() 取到最小值。此时
取到最小值。此时![]()
综上所述,当![]() 即
即![]() 时,函数有最大值10;
时,函数有最大值10;
当![]() 时,函数有最小值6
…… 12分
时,函数有最小值6
…… 12分
暑假作业十一参考答案
1.![]() ;2.
;2.![]() ;3.
;3. ![]() ; 4.7; 5. 3+cos2x; 6.
; 4.7; 5. 3+cos2x; 6.![]() ; 7.
; 7.![]() ;
;
8.![]() ;9.
;9.![]() ; 10.
; 10.![]() ; 11.45度;12.(1)
; 11.45度;12.(1)![]() (2)
(2)![]() (3)
(3)![]() ;
;
13.![]() ;14. 解:由已知,得
;14. 解:由已知,得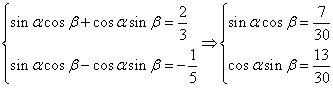
∴![]()
暑假作业十二参考答案
1.![]() 或
或![]() ; 2.锐角; 3.3或5; 4.等腰或直角; 5.
; 2.锐角; 3.3或5; 4.等腰或直角; 5. ![]() ; 6.
; 6.![]() ;
;
7.![]() ; 8. ①②④; 9.
; 8. ①②④; 9.![]()
![]() ; 10. ①④;
; 10. ①④;
11.解:(Ⅰ)因为![]() ,
,![]() ,
,
所以![]() .所以
.所以![]() .
.
(Ⅱ)在![]() 中,
中,![]() ,
,
由正弦定理![]() .故
.故![]()

![]() .·
.·

13. 解:(Ⅰ)由余弦定理得,![]() ,
,
又因为![]() 的面积等于
的面积等于![]() ,所以
,所以![]() ,得
,得![]() .
.
联立方程组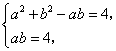 解得
解得![]() ,
,![]() .
.
(Ⅱ)由正弦定理,已知条件化为![]() ,
,
联立方程组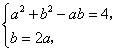 解得
解得![]() ,
,![]() .
.
所以![]() 的面积
的面积![]() .
.
14.如图:船按![]() 方向开出,
方向开出,![]() 方向为水流方向,以AC为一边,AB为对角线作平行四边形ACBD,其中
方向为水流方向,以AC为一边,AB为对角线作平行四边形ACBD,其中
![]()
在![]() ABC中,由余弦定理,得
ABC中,由余弦定理,得
![]() ,
,
所以 ![]()
因此,船的航行速度为
![]()
在![]() ABC中,由正弦定理得:
ABC中,由正弦定理得:
![]()
所以:![]()
所以
![]()
答
渡船应按北偏西![]() 的方向,并以
的方向,并以![]() 的速度航行。
的速度航行。
作业十三
1-4 CADA, 5-10: 菱形,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
11. 最大值10,最小值2
12. 答案:∵![]()
∴![]()
∴![]()
∴![]()
13.证明略
14.(1)![]() ;(2)不能构成平行四边形
;(2)不能构成平行四边形
作业十四:
1-3 : CAC
4-10 : ②③ , ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
11. x=2, y= -1, 面积16
12. ![]() 13.(1)
13.(1)![]() ; (2)
; (2)![]()
即![]() 时,
时,![]() 取最小值, 此时
取最小值, 此时![]()
14.(1)![]() ;(2)
;(2)![]()
暑假作业十五部分答案
7. ![]() ;9. n
.2n–1 ;10. (2,0)
;9. n
.2n–1 ;10. (2,0)
14. 解:(I)证明:首先,由![]() 中元素构成的有序数对
中元素构成的有序数对![]() 共有
共有![]() 个.
个.
因为![]() ,所以
,所以![]() ;
;
又因为当![]() 时,
时,![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() .
.
从而,集合![]() 中元素的个数最多为
中元素的个数最多为![]() ,
,
即![]() .
.
(II)解:![]() ,证明如下:
,证明如下:
(1)对于![]() ,根据定义,
,根据定义,![]() ,
,![]() ,且
,且![]() ,从而
,从而![]() .
.
如果![]() 与
与![]() 是
是![]() 的不同元素,那么
的不同元素,那么![]() 与
与![]() 中至少有一个不成立,从而
中至少有一个不成立,从而![]() 与
与![]() 中也至少有一个不成立.
中也至少有一个不成立.
故![]() 与
与![]() 也是
也是![]() 的不同元素.
的不同元素.
可见,![]() 中元素的个数不多于
中元素的个数不多于![]() 中元素的个数,即
中元素的个数,即![]() ,
,
(2)对于![]() ,根据定义,
,根据定义,![]() ,
,![]() ,且
,且![]() ,从而
,从而![]() .如果
.如果![]() 与
与![]() 是
是![]() 的不同元素,那么
的不同元素,那么![]() 与
与![]() 中至少有一个不成立,从而
中至少有一个不成立,从而![]() 与
与![]() 中也不至少有一个不成立,
中也不至少有一个不成立,
故![]() 与
与![]() 也是
也是![]() 的不同元素.
的不同元素.
可见,![]() 中元素的个数不多于
中元素的个数不多于![]() 中元素的个数,即
中元素的个数,即![]() ,
,
由(1)(2)可知,![]() .
.
十六部分答案
2.3
5.2009
8.7
9. ![]()
10. ①②③④
暑假作业十八参考答案
1.一
2.12
3.![]()
7. 当![]() 时,每间最大积是
时,每间最大积是![]()
8.D
9.4200 ![]()