高一数学立体几何提高复习

2008年暑假补课数学教案---------(必修二之立体几何部分)

洞口三中　方锦昌　

第二章 小结(1)(08年7月7日)　　　（1） 点、直线、平面的位置关系　

（一）知识回顾，整体认识

1、本章知识回顾

（1）空间点、线、面间的位置关系：

（2）直线、平面平行的判定及性质：

（3）直线、平面垂直的判定及性质：

（二）整合知识，发展思维

1、公理1——判定直线是否在平面内的依据；　 公理2——提供确定平面最基本的依据；

公理3——判定两个平面交线位置的依据；　 公理4——判定空间直线之间平行的依据。

2、空间问题解决的重要思想方法：化空间问题为平面问题；

3、空间平行、垂直之间的转化与联系：

（三）应用举例，深化巩固

例 1、已知，为两条不同的直线，，为两个不同的平面，则下列命题中正确的是（ D ） A ．　　B．

C．　　　　　　　　 D．

2、设为两条直线，为两个平面，下列四个命题中，正确的命题是（　D　）

Ａ．若与所成的角相等，则　　 Ｂ．若，，则　　

 Ｃ．若，则　　 Ｄ．若，，则

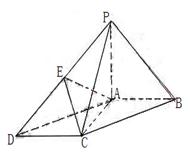
3、如图，在底面为平行四边形的四棱锥中，，平面，且，点是的中点.

求证：平面；

解:　 证OE∥PB

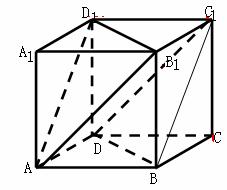4、如图，在正方体ABCD-A₁B₁C₁D₁　中，求证：面AB₁D₁∥面BDC₁

解:通过两相交直线的平行可证明.

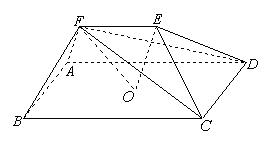5．如图，在五面体中，点是矩形的对角线的交点，面是等边三角形，棱．（1）证明//平面；

解:证 FO∥EG

巩固训练：A组题：　 一、选择题：1．有四个命题：

(1)、直线在平面内，直线在平面内，且相交，则平面与重合;(2)、直线共面，直线相交，则直线共面。（3）、直线在平面内，与平行，则与面没有公共点；（4）、有三个公共点的两个平面一定重合；以上命题中错误命题的个数是(　C )

（（A）1个　 （B）2个　　（C）3个　　 （D）4个

2、已知，则等于（　B ）

 A 　　　B 　　 C　　　 D 以上几个都不对

3、如果直线直线b，且a//平面，那么b与的位置关系是（D　）

 A  相交　　 B 　　C　　 D

4、下列语句中，正确的个数为 （　A ）

（1）一条直线和另一条直线平行，它和经过另一条直线的任何平面平行；（2）一条直线和一个平面平行，它和这个平面内的任何直线平行；（3）过平面外一点和这个平面平行的直线只有一条；（4）平行于同一个平面的两条直线互相平行　　　　A  0　　　　　　B   1　　 　　　　C　 2　　　　　  D　3

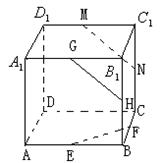5、如右图，ABCD--是正方体，分别为所在棱的中点，则下列结论正确的是（ B ）　和为平行直线，和为相交直线

和为平行直线，和为相交直线

和为相交直线，和为异面直线

和为异面直线，和也是异面直线

二、填空题：

6、已知是两条异面直线，a上有三个点，b上有两个点，这些点可确定　　5　个平面

7．不共线的三个平面两两相交，可将空间分成 7或者8　　　个部分．

8、在正方体的六个表面中，与异面组成角的对角线共有　 4　 条。

9、长方体ABCD--中，已知三条棱，，，则异面直线与所成的角的度数为　 60°　

三、解答题：

10．已知在正方体中，E、F分别是的中点，求证：平面平面

11、已知E、F、G、M分别是四面体的棱AD、CD、BD、BC的中点，

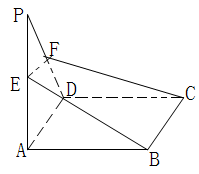求证：AM面EFG

12、如图，四边形ABCD是矩形，面ABCD，过BC作平面BCFE交AP于E，

　 交DP于F，求证：四边形BCFE是梯形

B组题：

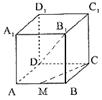四、选择题：13．A,b是异面直线，A ,B是a上的两点，C, D是b上的两点，M ,N分别是线段AC,BD的中点，则MN和a的位置关系为（ A　）

A 异面　 B平行　 C相交　　D以上三种关系都有可能

14．如图所示，在正方体中，M为AB的中点，则异面直线与CM所成角的余弦值为（　D  ）(A)　　　(B)　 　 C 　 　(D)

15、已知直线与直线垂直，平行于平面，则与平面的位置关系是（D　）

A．　　  B．　　  C．与平面相交　　D．以上都有可能

16、是空间四边形，分别是四条边的任意四点，则下列结论正确的是（ D　）A.和是相交直线　　　　B. EH和FG是平行直线

 C. 和是异面直线　　　D. 以上情况都有可能

17、正方体中，、、分别是、、的中点．那么正方体的过、、的截面图形是（　 D　）

A．三角形　　　　B．四边形　　　　C．五边形　　　　D．六边形

五、填空题：

18．三个平面将空间最少分成部分，最多分成部分，则等于　 12　　　．

19．三条直线中有两条平行，第三条和这两条都相交时确定　　1　个平面；三条直线交于一点时可确定__1或者3　　　个平面；三条直线互相平行时，最多可确定　　3　 个平面。

20．连接抛物线上任意四点组成的四边形可能是　②③⑤　　　 （填写所有正确选项的序号） 　　①菱形　②有3条边相等的四边形　　③梯形　　　　　　　④平行四边形　　　⑤有一组对角相等的四边形

21．已知m、n是不同的直线，是不重合的平面，给出下列命题：①若则②若则　　③m、n是两条异面直线，若则上面命题中，真命题的序号是_____③_______(写出所有真命题的序号)

六、解答题：

22．正方体ABCD—A₁B₁C₁D₁的棱长为　（1）、求△AB₁D₁的面积；（2）、求三棱锥的体积。

　　　　　　　　解、①　②

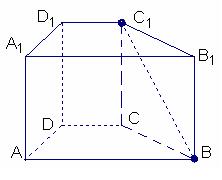23．已知直四棱柱中，，底面是直角梯形，，，，，，求异面直线与所成的角的余弦值　　　 (解:为)

24、过正方体的棱作一平面交平面于，求证：//

第二章 小结（2）(08年7月8日)

（一）知识回顾，整体认识

1. 直线和平面垂直的判定及性质；　

 2. 平面和平面垂直的判定及性质.

（二）应用举例，深化巩固

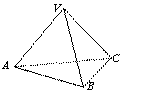
1、如图，在三棱锥V-ABC中，VA＝VC，AB＝BC，求证：VB⊥AC．

2、过△ABC所在平面a外一点P， 作PO⊥a，垂足为O，连接PA，PB，PC.

(1)若PA＝PB＝PC，∠C＝90°，则点O 是AB边的　　　中　　　 点．

(2)若PA＝PB＝PC，则点O是△ABC的　　　　　  外　　 心．

(3)若PA⊥PB，PB⊥PC，PC⊥PA，则点O是△ABC的　　　　  垂　　　心．

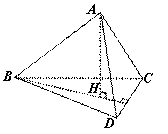3、如图，已知空间四边形ABCD的边BC＝AC，AD＝BD，引BE⊥CD，E为垂足，作AH⊥BE于H. 求证： AH⊥平面BCD．

4. 已知ABCD是正方形，PA⊥平面ABCD， BE⊥PC，E为垂足.

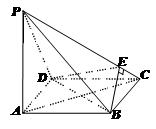求证：平面BDE⊥平面PBC．

解:PC⊥面BDE

训练提高练习:　　　　C组题：七、选择或填空题：

25、平面平面，平面平面，平面平面，若，

则与的位置关系是（ D　 ）

A．与异面　　B．与相交　　C．至少与中的一条相交　　　D．与都平行

26．平面过直线外的两点，若要这个平面与平行，则这样的平面有　　 （　D　）

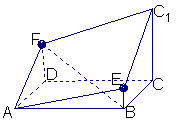A　无数个　　　　B 一个　　　　　C不存在　　　　  D上述情况都有可能

八、解答题：

27．如图所示的多面体是由底面为ABCD的长方体被截面AEC₁F所截面而得到的，其中AB=4，BC=2，CC₁=3，BE=1求BF的长；　　

解:(2注意到AE∥FC₁)

28．两个全等的正方形ABCD和ABEF所在平面相交于AB，M∈AC，N∈FB，且AM=FN，求证：MN∥平面BCE。

29．（08高考 宁夏18）（本小题满分12分）如下的三个图中，上面的是一个长方体截去一个角所得多面体的直观图．它的正视图和侧视图在下面画出（单位：cm）（Ⅰ）在正视图下面，按照画三视图的要求画出该多面体的俯视图；（Ⅱ）按照给出的尺寸，求该多面体的体积；（Ⅲ）在所给直观图中连结，证明：面．

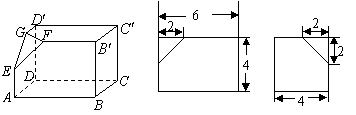
解:俯视图为:

第二章 小结（3）(08年7月9日)

（一）知识回顾，整体认识

1. 异面直线所成角；　

2. 直线与平面所成角；

3. 两平面所成角.

（二）应用举例，深化巩固

例1. 已知空间四边形ABCD中，P、Q分别是AB、CD的中点，且PQ＝3，AC＝4，BD＝2  ，　AC与BD所成角的大小．

例2. 已知四面体ABCD的各棱长均相等，E、F分别为AB、CD的中点，求EF与AC所成角的大小．

例3. 在四面体ABCD中，平面ABD⊥平面BCD，△ABD为等边三角形，CD⊥BD，∠DBC＝30^o．

(1 )求二面角A-DC-B的大小；　　 (2) 求二面角A-BC-D的平面角的正切值；　　(3) 求二面角D-AB-C的平面角的正切值.

解:　注意三垂线法的应用与讲解.

例4. 圆台上、下底面半径分别为2、4，O₁A₁、OB分别为上、下底面的半径，二面角A₁-OO₁-B是60o，圆台母线与底面成60^o角.　 (1) 求A₁B和OO₁所成角的正切值；　　(2) 求圆台的侧面积及体积.

解; 注意 概念的转化,　实为一个三棱台的问题.

例5. 在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD＝90^o，PA⊥底面ABCD，且PA＝AD＝AB＝2BC，M、N分别为PC、PB的中点，求CD与平面ADMN所成角的正弦.

解:注意到BN⊥面ADMN

第二章小结（4）—— 空间距离(08年7月10日)

一、复习目的:　　

 1．掌握两条直线所成的角和距离的概念及等角定理；（对于异面直线的距离，只要求会计算已给出公垂线时的距离）。　　 2．掌握点、直线到平面的距离，直线和平面所成的角；

3．掌握平行平面间的距离，会求二面角及其平面角；

二、教学过程

1．基本知识：　（1）空间中的距离是立体几何的重要内容，其内容主要包括：点点距，点线距，点面距，线线距，线面距，面面距。其中重点是点点距、点线距、点面距以及两异面直线间的距离．因此，掌握点、线、面之间距离的概念，理解距离的垂直性和最近性，理解距离都指相应线段的长度，懂得几种距离之间的转化关系，所有这些都是十分重要的。

（2）求距离的重点在点到平面的距离，直线到平面的距离和两个平面的距离可以转化成点到平面的距离，一个点到平面的距离也可以转化成另外一个点到这个平面的距离。

（3）点到平面的距离

平面外一点P 在该平面上的射影为P′，则线段PP′的长度就是点到平面的距离；

求法：1“一找二证三求”，三步都必须要清楚地写出来。　　　　  2等体积法。

（4）直线与平面的距离：一条直线和一个平面平行，这条直线上任意一点到平面的距离，叫做这条直线和平面的距离；

（5）平行平面间的距离：两个平行平面的公垂线段的长度，叫做两个平行平面的距离。

求距离的一般方法和步骤：应用各种距离之间的转化关系和“平行移动”的思想方法，把所求的距离转化为点点距、点线距或点面距求之，其一般步骤是：

①找出或作出表示有关距离的线段；　　②证明它符合定义；　　 ③归到解某个三角形．若表示距离的线段不容易找出或作出，可用体积等积法计算求之。

2、举例分析

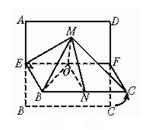
例1、正方形ABCD的边长是2，E、F分别是AB和CD的中点，将正方形沿EF折成直二面角（如图所示）.M为矩形AEFD内一点，如果∠MBE=∠MBC，MB和平面BCFE所成角的正切值为，那么点M到直线EF的距离为　　。

例2．如图，四面体ABCD中，O、E分别BD、BC的中点，CA=CB=CD=BD=2。△ABD为等腰直角三角形。　　 （Ⅰ）求证：AO⊥平面BCD；　　（Ⅱ）求异面直线AB与CD所成角的余弦值；　　　　

（Ⅲ）求点E到平面ACD的距离。

解:注意平移之后再求距离的问题的应用.

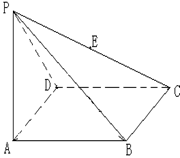★【例题3】、如图,四棱锥的底面为菱形,且,,的中点.

(1)求直线与平面所成角的大小;　(2)求二面角的平面角的正切值;　 (3)在线段上是否存在一点,使成立?如果存在,求出的长;如果不存在,请说明理由.

解;本题最好使用几何法加以处理.

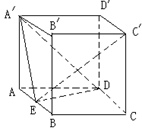★【例题4】、如图,直平行六面体ABCD-A′B′C′D′的底面ABCD是边长为2的菱形,∠BAD=60°, E为AB的中点,二面角A′-ED-A为60°；

（1）、求证：平面A′ ED⊥平面ABB′A′；（2）、求二面角A′-ED-C′ 的大小；

（3）、求点C′ 到平面A′ED的距离。

解:本题第一问最好用几何法处理,第二问要注意到A′E⊥ED且C′D⊥ED,再用向量法处理;第三问则最好用向量法去处理.

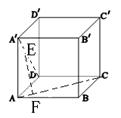
【例题5】如图，在正方体ABCD—A′B′C′D′中，EF是异面直线AC与A′D的公垂线,则由正方体的八个顶点所连接的直线中,与EF平行的直线( A　) 

 A 有且只有一条　　　　B 有二条　　　 C　有四条　　　　 D　不存在

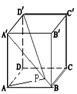★【例题6】如图所示，在单位正方体ABCD-A′B′C′D′中，若四边形A′ABB′的对角线A′B上存在一点P使得AP+D′P最小，则AP+D′P的最小值是_____

解:考虑图形的翻折去处理.

一、两个平面垂直：

1、生活实例：教室中黑板面与地面间关系，打开的手提电脑……

2、几何意义：①直二面角　 ②法向量互相垂直的两个平面

二、判定方法：

方法1：判定定理：①文字表述　　　　②数学符号语言：aα 且a⊥β则α⊥β

→思路：在一个平面之内找出一条直线，证明它垂直于另一个平面

方法2：  求出该二面角的平面角等于90度。　　方法3：　 向量法：计算出两个平面的法向量·=0

三、性质：

性质定理：①文字表述 ②数学符号语言：α⊥β aα α∩β=L a⊥L 即a⊥β

　　思路：空间做垂线时，找垂足位置的依据——要做垂线，先找垂直平面与交线。垂面可见，垂足可做。

（3）基础演练：

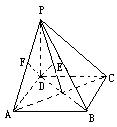题1：如图：在四棱锥P-ABCD中，底面ABCD为正方形，PD⊥底面ABCD， 且PD=AD=1，则　　　　　

（1）直线BC到平面PAD的距离为______1_____（找）

（2）点D到平面PAC的距离为________/3__（做）

（3）点C到平面PAB的距离为______/2____（先转化→再做）

题2：填空：

（1）平面α∥平面β， 平面β⊥平面γ，则平面α与平面γ

　　 的位置关系为_______a⊥γ__

 (2) 平面α⊥平面β, 平面β⊥平面γ，则平面α与平面γ的位置关系为____a∥γ或a与γ相交_____.

 (3)直线a⊥平面α， 直线a⊥平面β，则平面α与平面β的位置关系为____a∥b_____.

（4）直线a⊥平面α， 直线b⊥平面β，直线a⊥直线b,则平面α与平面β的位置关系___a⊥b.

题3：已知m、n、l为不同的直线，α、β、γ为不同的平面，则真命题序号有__①②④_______

①α⊥γ β∥γ 则α⊥β　　②l∥α l⊥β则α⊥β　　③m⊥α nβ m⊥n 则α⊥β

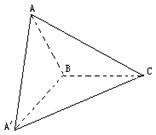④α∥β　　m⊥α　n∥β 则m⊥n　　⑤α⊥β α∩β=m 　n⊥m　则n⊥β

⑥β∩γ=l l∥α　mα m⊥γ 则l⊥m　m∥β

题４：三角形ABC中　AB=BC=1， ∠ABC=120^o, 将三角形ABC所在平面沿BC边所在的直线旋转90 ^o之后，得到平面A′BC ，

（1）求AA′与平面A′BC所成角的大小？

（2）求二面角A-BA′-C的平面角的大小？

（3）求点B到平面AA′C的距离？

（4）巩固练习：

题1、斜三棱柱ABC-A′B′C′中∠BAC=90 ^o， 且B C′⊥AC，过C′

做C′H⊥平面ABC，垂足为H，则（ B　　 ）

A、点H落于直线AC上　　　　 B、点H落于直线AB上　　　　　　　　　　

C、点H落于直线BC上　　　　 D、点H落于三角形ABC之内

题2、在四棱锥P-ABCD中，PA⊥底面ABCD，且ABCD为菱形，M在PC边上滑动，则当点

M满足___MB⊥PC______时平面MBD⊥平面PCD。

题3：四棱锥P-ABCD中，侧面PCD为正△，且与底面ABCD垂直，

已知底面ABCD为菱形，其边长为2，且∠ADC=60 ^o，M为PB中点。

①　　 求证：PA⊥CD

②　　 求PB与底面ABCD所成的角

③　　 求证：平面CDM⊥平面PAB。

解: 注意到PA⊥面CDMN

（5）回味高考：

题1：（湖南05年文科4题）正方体ABCD-A′B′C′D′中棱长为1，E为A′B′中点，则E到平面ABC′D′距离为（ B ）

A   B C   D

题2：（湖南05年文科15题）平面α、β和直线m，

给出条件①m∥α ②m⊥α ③mα ④α⊥β　⑤α∥β 则

(1)当满足条件___③⑤______时有m∥β　

(2)当满足条件____②⑤_____时有m⊥β

 题3：（06年全国文7题）平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角为45 ^o、30 ^o,过A、B分别做两平面交线的垂线，垂足为A′、B′，设AB=12，则A′B′=（　B  ）A、4　　 B、6　　 C、8　　　 D、9

归纳总结：（2）求距离的一般方法和步骤是：一作——作出表示距离的线段；二证——证明它就是所要求的距离；三算——计算其值．此外，我们还常用体积法求点到平面的距离．

（3）求距离的关键是化归。即空间距离与角向平面距离与角化归，各种具体方法如下：

①求空间中两点间的距离，一般转化为解直角三角形或斜三角形。

②求点到直线的距离和点到平面的距离，一般转化为求直角三角形斜边上的高；或利用三棱锥的底面与顶点的轮换性转化为三棱锥的高，即用体积法。

　　　　　　　　　　　　　　　 高一数学必修2立体几何测试题(自测用)

一、选择题(50分)：

1、线段在平面内，则直线与平面的位置关系是　　

A、　　　 B、　　  C、由线段的长短而定 D、以上都不对

2、下列说法正确的是　　　　　　

A、三点确定一个平面　　　　　　　  B、四边形一定是平面图形　　

C、梯形一定是平面图形　　　　　　  D、平面和平面有不同在一条直线上的三个交点

3、垂直于同一条直线的两条直线一定　

A、平行　　　　　 B、相交　　　　 C、异面　　　　　　　　  D、以上都有可能

4、在正方体中，下列几种说法正确的是　　

A、　　B、　 C、与成角　　D、与成角

5、若直线∥平面，直线，则与的位置关系是　　 

A、 ∥　　　　 B、与异面　　 C、与相交　　　　　　 D、与没有公共点

6、下列命题中：（1）、平行于同一直线的两个平面平行；（2）、平行于同一平面的两个平面平行；

（3）、垂直于同一直线的两直线平行；（4）、垂直于同一平面的两直线平行.其中正确的个数有

A、1　　　　　　 B、2　　　　　　  C、3　　　　　　　　  D、4

7、在空间四边形各边上分别取四点，如果与能相交于点，那么(　 )　　　　　　　　　　　　　 A、点必在直线上　　　　　　　　　　　　 B、点必在直线BD上

C、点必在平面内　　　　　　　　  D、点必在平面外

8、a，b，c表示直线，M表示平面，给出下列四个命题：①若a∥M，b∥M，则a∥b；②若bM，

a∥b，则a∥M；③若a⊥c，b⊥c，则a∥b；④若a⊥M，b⊥M，则a∥b.其中正确命题的个数有

　A、0个　　　　　 B、1个 　　　　　  C、2个　　　　　　　  D、3个

9、一个棱柱是正四棱柱的条件是(　 )　底面是正方形，有两个侧面是矩形　B、底面是正方形，有两个侧面垂直于底面　C、底面是菱形，且有一个顶点处的三条棱两两垂直　D、每个侧面都是全等矩形的四棱柱

10、在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是：　A、　　　　　 B、　　　　 、　　　 D、

二、填空题：

11、已知二面角的平面角是锐角，内一点到的距离为3，点C到棱的距离为4，那么的值等于______

12、如图:直三棱柱ABC—A₁B₁C₁的体积为V，点P、Q分别在侧棱AA₁和

CC₁上，AP=C₁Q，则四棱锥B—APQC的体积为______

13、(1)、等体积的球和正方体,它们的表面积的大小关系是_____(填”大于、小于或等于”).

(2)、正方体中，平面和平面的位置关系为　　　

14、已知垂直平行四边形所在平面，若，平行则四边形 一定是　　　　　 .

15、如图，在直四棱柱A₁B₁C₁ D₁－ABCD中，当底面四边形ABCD满足条件_________时，有A₁ B⊥B₁ D₁．(注：填上你认为正确的一种条件即可，不必考虑所有可能的情形.)

三、解答题：　

 16、已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.(10分)

17、已知中，面，，求证：面．

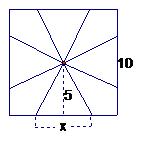
18、一块边长为10的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积与的函数关系式,并求出函数的定义域. (12分)

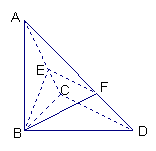
19、已知正方体，是底对角线的交点. 求证：（１）∥面；

　（2 ）面．　

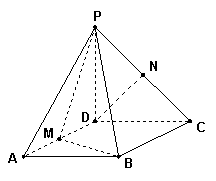
20、已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，

∠ADB=60°，E、F分别是AC、AD上的动点，且

　　　 （Ⅰ）求证：不论λ为何值，总有平面BEF⊥平面ABC；

　　　 （Ⅱ）当λ为何值时，平面BEF⊥平面ACD？ (14分)

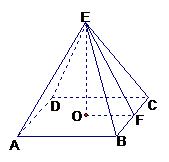
21、已知四棱锥P-ABCD，底面ABCD是、边长为的

菱形，又，且PD=CD，点M、N分别是棱AD、PC的中点．　　（1）证明：DN//平面PMB；

　　　　（2）证明：平面PMB平面PAD；

　　　　（3）求点A到平面PMB的距离．

参考答案：ACDDD　 BCBDD　 DB　　13、　　 14、　　 15、　　  16、　　17、解:设圆台的母线长为,则 圆台的上底面面积为　圆台的上底面面积为　　　 所以圆台的底面面积为又圆台的侧面积　于是　　即为所求.　 20、解　依题意函数的定义域为　　22、证明：（Ⅰ）∵AB⊥平面BCD， ∴AB⊥CD，∵CD⊥BC且AB∩BC=B， ∴CD⊥平面ABC.又∴不论λ为何值，恒有EF∥CD，∴EF⊥平面ABC，EF平面BEF, 　　∴不论λ为何值恒有平面BEF⊥平面ABC. （Ⅱ）由（Ⅰ）知，BE⊥EF，又平面BEF⊥平面ACD，∴BE⊥平面ACD，∴BE⊥AC.　∵BC=CD=1，∠BCD=90°，∠ADB=60°，∴由AB²=AE·AC 得　 故当时，平面BEF⊥平面ACD.