班次______姓名______;学号______ 湖南省省级示范性高中……洞口三中数学必修二之立体几何测试
撰稿: 方锦昌 易传庚
一、选择题(本大题共10小题,每小题5分,共50分)
1.若直线a不平行于平面![]() ,则下列结论成立的是( )
,则下列结论成立的是( )
A. ![]() 内所有的直线都与a异面; B.
内所有的直线都与a异面; B. ![]() 内不存在与a平行的直线;
内不存在与a平行的直线;
C. ![]() 内所有的直线都与a相交; D.直线a与平面
内所有的直线都与a相交; D.直线a与平面![]() 有公共点.
有公共点.
2.已知两个平面垂直,下列命题( )
①一个平面内的已知直线必垂直于另一个平面的任意一条直线;
②一个平面内的已知直线必垂直于另一个平面的无数条直线;
③一个平面内的任一条直线必垂直于另一个平面;
④过一个平面内任意一点作交线的垂线,则垂线必垂直于另一个平面.
其中正确的个数是: A.3 B.2 C.1 D.0
3.空间四边形ABCD中,若![]() ,则
,则![]() 与
与![]() 所成角为( )
所成角为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4. 给出下列命题:( )
(1)直线a与平面![]() 不平行,则a与平面
不平行,则a与平面![]() 内的所有直线都不平行;
内的所有直线都不平行;
(2)直线a与平面![]() 不垂直,则a与平面
不垂直,则a与平面![]() 内的所有直线都不垂直;
内的所有直线都不垂直;
(3)异面直线a、b不垂直,则过a的任何平面与b都不垂直;
(4)若直线a和b共面,直线b和c共面,则a和c共面
其中错误命题的个数为:(A)0 (B) 1 (C)2 (D)3
5.正方体ABCD-A1B1C1D1中,与对角线AC1异面的棱有( )条
A 3 B 4 C 6 D 8
6. 点P为ΔABC所在平面外一点,PO⊥平面ABC,垂足为O,若PA=PB=PC,则点O是ΔABC的( )
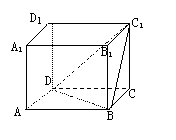 (A)内心
(B)外心 (C)重心
(D)垂心
(A)内心
(B)外心 (C)重心
(D)垂心
7.如图长方体中,AB=AD=2![]() ,CC1=
,CC1=![]() ,则二面角C1—BD—C的大小为( )
,则二面角C1—BD—C的大小为( )
(A)300 (B)450 (C)600 (D)900
8.直线a,b,c及平面α,β,γ,下列命题正确的是( )
A、若a![]() α,b
α,b![]() α,c⊥a, c⊥b 则c⊥α B、若b
α,c⊥a, c⊥b 则c⊥α B、若b![]() α, a//b 则 a//α
α, a//b 则 a//α
 C、若a//α,α∩β=b
则a//b D、若a⊥α, b⊥α 则a//b
C、若a//α,α∩β=b
则a//b D、若a⊥α, b⊥α 则a//b
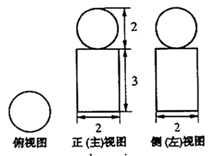
9.(08高考山东卷6题)右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
(A)9π (B)10π (C)11π (D)12π
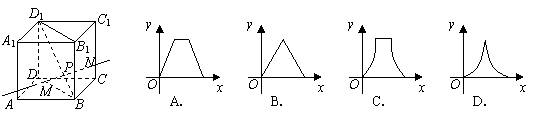
10、(08高考北京卷8题)如图,动点![]() 在正方体
在正方体![]() 的对角线
的对角线![]() 上.过点
上.过点![]() 作垂直于平面
作垂直于平面![]() 的直线,与正方体表面相交于
的直线,与正方体表面相交于![]() .设
.设![]() ,
,![]() ,则函数
,则函数![]() 的图象大致是( )
的图象大致是( )
二、填空题 11.已知直线a//平面![]() ,平面
,平面![]() //平面
//平面![]() ,则a与
,则a与![]() 的位置关系为
的位置关系为
 12.已知直线a⊥直线b, a//平面
12.已知直线a⊥直线b, a//平面![]() ,则b与
,则b与![]() 的位置关系为
的位置关系为
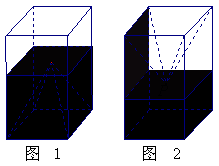
13.(08江苏16题)如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有![]() 升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点![]() (图2)。有下列四个命题:A.正四棱锥的高等于正四棱柱高的一半
(图2)。有下列四个命题:A.正四棱锥的高等于正四棱柱高的一半
B.将容器侧面水平放置时,水面也恰好过点![]()
C.任意摆放该容器,当水面静止时,水面都恰好经过点![]()
 D.若往容器内再注入
D.若往容器内再注入![]() 升水,则容器恰好能装满;其中真命题的代号是:
升水,则容器恰好能装满;其中真命题的代号是:
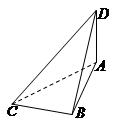
14.(浙江卷14)如图,已知球O点面上四点A、B、C、D,DA![]() 平面ABC,AB
平面ABC,AB![]() BC, DA=AB=BC=
BC, DA=AB=BC=![]() ,则球O点体积等于___________。
,则球O点体积等于___________。
 15、在正三棱锥
15、在正三棱锥![]() (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中,![]() ,过
,过![]() 作与
作与![]() 分别交于
分别交于![]() 和
和![]() 的截面,则截面
的截面,则截面![]()
![]() 的周长的最小值是________
的周长的最小值是________![]()
三、解答题
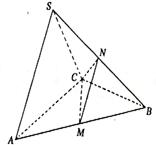
16、在三棱锥![]() 中,△
中,△![]() 是边长为
是边长为![]() 的正三角形,平面
的正三角形,平面![]() 平面
平面![]() ,
,![]() 、
、![]() 分别为
分别为![]() 的中点
的中点![]() (Ⅰ)证明:
(Ⅰ)证明:![]() ⊥
⊥![]() ;(Ⅱ)求二面角
;(Ⅱ)求二面角![]() -
-![]() -
-![]() 的大小;(Ⅲ)求点
的大小;(Ⅲ)求点![]() 到平面
到平面![]() 的距离
的距离![]()
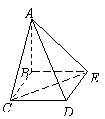 17、(08高考·全国一18题)四棱锥
17、(08高考·全国一18题)四棱锥![]() 中,底面
中,底面![]() 为矩形,侧面
为矩形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() .(Ⅰ)证明:
.(Ⅰ)证明:![]() ;(Ⅱ)设
;(Ⅱ)设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的大小.
的大小.
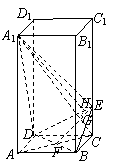
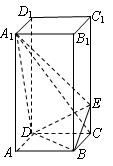 18、(08全国二19)如图,正四棱柱
18、(08全国二19)如图,正四棱柱![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上且
上且![]() .(Ⅰ)证明:
.(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
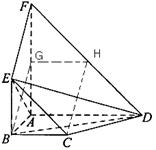
19、(08四川卷19)
如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 与
与![]() 都是直角梯形,
都是直角梯形,
![]()
![]()
![]() ,
,![]()
![]()
![]() (Ⅰ)证明:
(Ⅰ)证明:![]() 四点共面;
四点共面;
(Ⅱ)设![]() ,求二面角
,求二面角![]() 的大小;
的大小;
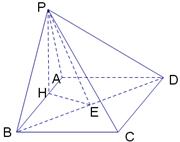 20、(08高考天津卷19题·满分12分)如图,在四棱锥
20、(08高考天津卷19题·满分12分)如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形.已知
是矩形.已知![]() .
.
(Ⅰ)证明![]() 平面
平面![]() ;目 (Ⅱ)求异面直线
;目 (Ⅱ)求异面直线![]() 与
与![]() 所成的角的大小; (Ⅲ)求二面角
所成的角的大小; (Ⅲ)求二面角![]() 的大小.
的大小.
21、(08高考·重庆19题·满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)
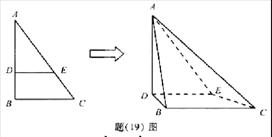 如题(19)图,在
如题(19)图,在![]() 中,B=
中,B=![]() ,AC=
,AC=![]() ,D、E两点分别在AB、AC上.使
,D、E两点分别在AB、AC上.使![]() ,DE=3.现将
,DE=3.现将![]() 沿DE折成直二角角,求:
沿DE折成直二角角,求:
(Ⅰ)异面直线AD与BC的距离;
(Ⅱ)二面角A-EC-B的大小(用反三角函数表示).
参考答案
1.D;2.C;3.D;4.D;5.C;6.B;7.A;8.D;9.D;10.B
11.平行或在平面内; 12. 平行或在平面内; 13.BD 14.9π/2
15题、![]() 沿着
沿着![]() 将正三棱锥
将正三棱锥![]() 侧面展开,则
侧面展开,则![]() 共线,且
共线,且![]()
16、略; 17题解:(1)取![]() 中点
中点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
又面![]() 面
面![]() ,
,![]()
![]() 面
面![]() ,
,![]()
![]() .
.![]() ,
,
![]()
![]() ,
,![]() ,即
,即![]() ,
,![]() 面
面![]() ,
,![]() .
.
(2)在面![]() 内过
内过![]() 点作
点作![]() 的垂线,垂足为
的垂线,垂足为![]() .
.![]()
![]() ,
,![]() ,
,![]() 面
面![]() ,
,![]() ,则
,则![]() 即为所求二面角的平面角.
即为所求二面角的平面角.![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
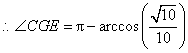 ,即二面角
,即二面角![]() 的大小
的大小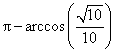 .
.
18依题设知![]() ,
,![]() .(Ⅰ)连结
.(Ⅰ)连结![]() 交
交![]() 于点
于点![]() ,则
,则![]() .
.
由三垂线定理知,![]() . 在平面
. 在平面![]() 内,连结
内,连结![]() 交
交![]() 于点
于点![]() ,
,
由于![]() ,故
,故![]() ,
,![]() ,
,
![]() 与
与![]() 互余.于是
互余.于是![]() .
.![]() 与平面
与平面![]() 内两条相交直线
内两条相交直线![]() 都垂直,
都垂直,
所以![]()
![]() 平面
平面![]() .(Ⅱ)作
.(Ⅱ)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .由三垂线定理知
.由三垂线定理知![]() ,
,
 故
故![]() 是二面角
是二面角![]() 的平面角.
的平面角. ![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() .又
.又![]() ,
,![]() .
.![]() .所以二面角
.所以二面角![]() 的大小为
的大小为![]() .
.
19(Ⅰ)延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,由
,由![]()
![]()
![]() 得
得 ![]()
延长![]() 交
交![]() 的延长线于
的延长线于![]() 同理可得
同理可得![]()
故![]() ,即
,即![]() 与
与![]() 重合,因此直线
重合,因此直线![]() 相交于点
相交于点![]() ,即
,即![]() 四点共面。
四点共面。
(Ⅱ)设![]() ,则
,则![]() ,
,![]() 取
取![]() 中点
中点![]() ,则
,则![]() ,又由已知得,
,又由已知得,![]() 平面
平面![]() 故
故![]() ,
,![]() 与平面
与平面![]() 内两相交直线
内两相交直线![]() 都垂直。所以
都垂直。所以![]() 平面
平面![]() ,作
,作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() 由三垂线定理知
由三垂线定理知![]() 为二面角
为二面角![]() 的平面角。
的平面角。
![]() 故
故![]() 所以二面角
所以二面角![]() 的大小
的大小![]()
20(Ⅰ)证明:在![]() 中,由题设
中,由题设![]() 可得
可得![]() 于是
于是![]() .在矩形
.在矩形![]() 中,
中,![]() .又
.又![]() ,所以
,所以![]() 平面
平面![]() .(Ⅱ)解:由题设,
.(Ⅱ)解:由题设,![]() ,所以
,所以![]() (或其补角)是异面直线
(或其补角)是异面直线![]() 与
与![]() 所成的角.在
所成的角.在![]() 中,由余弦定理得
中,由余弦定理得
![]()
由(Ⅰ)知![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,因而
,因而![]() ,于是
,于是![]() 是直角三角形,故
是直角三角形,故![]() .所以异面直线
.所以异面直线![]() 与
与![]() 所成的角的大小为
所成的角的大小为![]() .
.
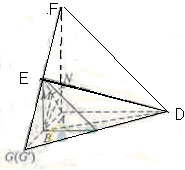
(Ⅲ)解:过点P做![]() 于H,过点H做
于H,过点H做![]() 于E,连结PE因为
于E,连结PE因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .又
.又![]() ,因而
,因而![]() 平面
平面![]() ,故HE为PE再平面ABCD内的射影.由三垂线定理可知,
,故HE为PE再平面ABCD内的射影.由三垂线定理可知,![]() ,从而
,从而![]() 是二面角
是二面角![]() 的平面角。由题设可得,
的平面角。由题设可得,
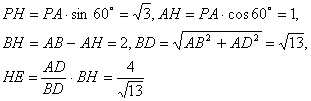 于是再
于是再![]() 中,
中,![]()
所以二面角![]() 的大小为
的大小为![]() .
.
21.(Ⅰ)在答(19)图1中,因![]() ,故BE∥BC.又因B=90°,从而AD⊥DE.在第(19)图2中,因A-DE-B是直二面角,AD⊥DE,故AD⊥底面DBCE,从而AD⊥DB.而DB⊥BC,故DB为异面直线AD与BC的公垂线.下求DB之长.在答(19)图1中,由
,故BE∥BC.又因B=90°,从而AD⊥DE.在第(19)图2中,因A-DE-B是直二面角,AD⊥DE,故AD⊥底面DBCE,从而AD⊥DB.而DB⊥BC,故DB为异面直线AD与BC的公垂线.下求DB之长.在答(19)图1中,由![]() ,得
,得![]() 又已知DE=3,从而
又已知DE=3,从而![]()
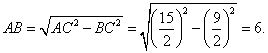 因
因![]() (Ⅱ)在第(19)图2中,过D作DF⊥CE,交CE的延长线于F,连接AF.由(1)知,AD⊥底面DBCE,由三垂线定理知AF⊥FC,故∠AFD为二面角A-BC-B的平面角.在底面DBCE中,∠DEF=∠BCE,
(Ⅱ)在第(19)图2中,过D作DF⊥CE,交CE的延长线于F,连接AF.由(1)知,AD⊥底面DBCE,由三垂线定理知AF⊥FC,故∠AFD为二面角A-BC-B的平面角.在底面DBCE中,∠DEF=∠BCE,![]() 因此
因此![]() 从而在Rt△DFE中,DE=3,
从而在Rt△DFE中,DE=3,![]() 在
在![]() 因此所求二面角A-EC-B的大小为arctan
因此所求二面角A-EC-B的大小为arctan![]()