![]() 高一数学第一学期期末统一考试
高一数学第一学期期末统一考试
数学理科试卷
本试卷分第I卷(选择题)、第II卷(非选择题)两部分。共100分,考试时间100分钟。
第I卷(选择题共40分)
注意事项:
1、答第I卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上。
2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上。
3、不可以使用计算器。
4、考试结束,将答题卡交回,试卷不用上交。
一、选择题(每小题4分,共40分)
1. 若![]() 为△ABC的内角,则下列函数中一定取正值的是( )
为△ABC的内角,则下列函数中一定取正值的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”( )
”( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.即不充分也不必要条件
3. ![]() 与
与![]() ,两数的等比中项是( )
,两数的等比中项是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 不等式![]() 的解集是
的解集是![]() ,则
,则![]() 的值是( )
的值是( )
A. 10 B. -10 C. 14 D. -14
5. 在△ABC中,![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6. 与椭圆![]() 有相同的两焦点且过点
有相同的两焦点且过点![]() 的双曲线方程是( )
的双曲线方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7. 若曲线![]() 的一条切线
的一条切线![]() 与直线
与直线![]() 垂直,则
垂直,则![]() 的方程为 ( )
的方程为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
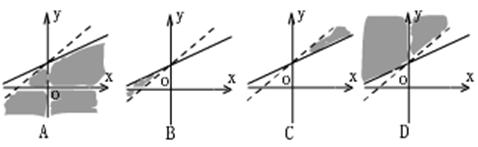
8. 不等式组![]() 表示的区域是( )
表示的区域是( )
9. 在等差数列![]() 中,
中,![]() 是方程
是方程![]() 的两个根,则
的两个根,则![]() 是( )
是( )
A.15 B.30 C.50 D.![]()
10.若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的右焦点重合,则
的右焦点重合,则![]() 的值为 ( )
的值为 ( )
A. 2 B.-2 C. 4 D. -4
|
数学理科试卷
第II卷(非选择题共60分)
| 题 号 | 二 | 15 | 16 | 17 | 18 | 19 | 总分 | 总分人 | 复分人 |
二、填空题(每小题4分,共16分)
11命题p:![]() 的否定是
的否定是
12.已知![]() ,则
,则![]() 的是小值为
.
的是小值为
.
13. 两个等差数列![]()
![]() 则
则![]() =
.
=
.
14设![]() ,则
,则![]() 的最大值为
的最大值为
三、解答题(共5小题. 15、16、17、18题各9分,19题8分,合计44分)
|
15. 在ΔABC中,角A、B、C所对的边是![]() 、
、![]() 、
、![]() ,
,
且![]() .
.
(1)求![]() 的值(4分)
的值(4分)
(2)若![]() =2,求ΔABC面积的最大值(5分)
=2,求ΔABC面积的最大值(5分)
|
16. 已知函数![]() .
.
⑴当![]() 时,求函数的单调区间(5分)
时,求函数的单调区间(5分)
⑵函数![]() 在
在![]() 处有极大值,求
处有极大值,求![]() 的值(4分)
的值(4分)
|
两点B,C,经过抛物线上一点P垂直于轴的直线和轴交于点Q,
求证:PQ是BC和OQ的比例中项.

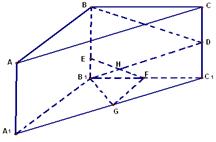
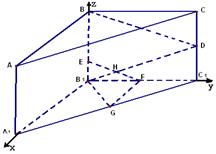
18.如图所示,在直三棱柱ABC—A1B1C1中,∠ABC=900,BC=2,CC1=4,EB1=1,D,F,G分别为CC1,B1C1,A1C1的中点,EF与B1D相交于点H.
(Ⅰ)求证:B1D⊥平面ABD;(3分)
(Ⅱ)求证:平面EGF∥平面ABD;(3分)
(Ⅲ)求平面EGF与平面ABD的距离.(3分)
 19. 设
19. 设![]() 为等比数列,
为等比数列,![]() ,
,![]() .
.
(1)求最小的自然数![]() ,使
,使![]() ;
;
(2)求和:![]() .
.
![]() 高一数学第一学期期末统一考试
高一数学第一学期期末统一考试
数学科试卷参考答案
一、选择题:AACDC BDBAC
二、填空题:11:![]() ;12:15; 13:
;12:15; 13:![]() ;14:
;14:![]()
三、解答题:
15.解:(1)∵![]() ,∴
,∴![]()
∴![]()
∵![]() 是ΔABC的内角,则
是ΔABC的内角,则![]()
∴![]() ;
;
(2)若![]() =2,ΔABC面积
=2,ΔABC面积![]()
又![]()
∴![]() ,∴
,∴![]()
∴![]()
当![]() 时,ΔABC面积
时,ΔABC面积![]() 为最大值.
为最大值.
16.解:⑴当![]() 时,
时, ![]() ;
;
![]() ,令
,令![]() ;得
;得 ![]()
|
|
|
|
| 1 |
|
|
| + | 0 | - | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
列表:
∴函数![]() 的单调增区间分别为
的单调增区间分别为![]() ,
,![]() ;
;
函数![]() 的单调减区间为
的单调减区间为![]() .
.
⑵∵![]() ;
;
∴![]()
∵函数![]() 在
在![]() 处有极大值,
处有极大值,
∴![]() ,即
,即![]() ;
;
∴![]()
17.证明:如图,设抛物线方程:![]() ,焦点为
,焦点为![]() ,
,
直线BC的方程为![]() ;解方程组
;解方程组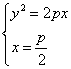 ,得
,得![]() ,
,
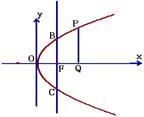 ∴B
∴B![]() ,C
,C![]() ,BC=
,BC=![]() ;
;
令P![]() ,由
,由![]() ,其中
,其中
OQ=![]() ,PQ=
,PQ=![]()
∵PQ2=![]() 2;BC
2;BC![]() OQ=
OQ=![]()
∴PQ2=BC![]() OQ;
OQ;
∴PQ是BC和OQ的比例中项.
18.(Ⅰ)证明:如图所示,建立空间直角坐标系,设A1(![]() ,0,0),则C1(0,2,0),F(0,1,0),E(0,0,1),A(
,0,0),则C1(0,2,0),F(0,1,0),E(0,0,1),A(![]() ,0,4),B(0,0,4),D(0,2,2),
,0,4),B(0,0,4),D(0,2,2),
 G(
G(![]() ,1,0),
,1,0),
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴B1D⊥AB,B1D⊥BD,又AB∩BD=B,
∴B1D⊥平面ABD.
(Ⅱ)证明:∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,
∴GF∥AB,EF∥BD,又GF∩EF=F,AB∩BD=B,
∴平面EGF∥平面ABD
(Ⅲ)解:由 (Ⅰ)、(Ⅱ)可知,DH为平面EFG与平面ABD的公垂线段,
设![]() ,则
,则![]() ,
,![]()
∵![]() 与
与![]() 共线,∴
共线,∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
因此,平面EGF与平面ABD的距离为![]()
19.解:(1)由已知条件得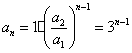 ,
,
因为![]() ,所以,使
,所以,使![]() 成立的最小自然数
成立的最小自然数![]() .
.
(2)因为![]() ,…………①
,…………①
![]() ,…………②
,…………②
![]() 得:
得:![]()
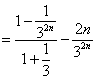
![]()
所以![]() .
.