高一数学第二学期期末统一考试卷
数学科试卷
本试卷分第I卷(选择题)、第II卷(非选择题)两部分.共100分,考试时间100分钟.
第Ⅰ卷(选择题 共40分)
注意事项:
1、答第I卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上.
2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上.
3、不可以使用计算器.
4、考试结束,将答题卡交回,试卷不用上交.
一、选择题:(本大题共10小题,每小题4分,共40分.)
1.已知![]() 是第一象限角,那么
是第一象限角,那么![]() 是
是
A.第一象限角 B.第二象限角
C.第一或第二象限角 D.第一或第三象限角
2.sin
(-![]() )=
)=
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
3.口袋内装有一些大小相同的红球、白球和黒球,从中摸出![]() 个球,摸出红球的概率是
个球,摸出红球的概率是![]() ,摸出白球的概率是
,摸出白球的概率是![]() ,那么摸出黒球的概率是
,那么摸出黒球的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列说法中,正确的是
A.数据5,4,4,3,5,2的众数是4
B.数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半
C.一组数据的标准差是这组数据的方差的平方
D.频率分布直方图中各小长方形的面积等于相应各组的频数
5.化简![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知![]() =5,
=5,![]() =4,
=4,![]() 与
与![]() 的夹角
的夹角![]() =120°则
=120°则![]() ·
·![]() 等于
等于
A.20 B.10 C.-10 D.-20
7.某中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270,并将整个编号依次分为10段.
如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是
A.②③都不能为系统抽样 B.②④都不能为分层抽样
C.①④都可能为系统抽样 D.①③都可能为分层抽样
8.为了得到函数![]() 的图象,只需把函数
的图象,只需把函数![]() 的图象
的图象
A.向左平行移动![]() 个单位长度 B. 向左平行移动
个单位长度 B. 向左平行移动![]() 个单位长度
个单位长度
C.向右平行移动![]() 个单位长度 D.向右平行移动
个单位长度 D.向右平行移动![]() 个单位长度
个单位长度
9.阅读下列程序:
INPUT ![]() ,
,![]()
![]()
![]()
![]()
![]()
PRINT ![]() ,
,![]()
END
当输入![]() =3,
=3,![]() =-5时计算结果为
=-5时计算结果为
A.![]() =3,
=3,![]() =-5
B.
=-5
B.![]() =
=![]() ,
,![]() =-
=-![]()
C.![]() =
=![]() ,
,![]() =-
=-![]() D.
D.![]() =-1,
=-1,![]() =4
=4
10.已知![]() 是
是![]() 所在平面内一点,
所在平面内一点,![]() 为
为![]() 边中点,且
边中点,且![]() ,那么
,那么
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共60分)
二、填空题:(本大题共4小题,每小题4分,共16分.把答案填在横线上.)
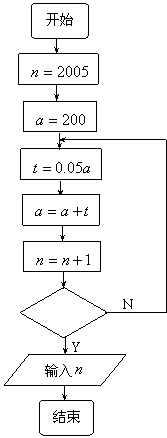 11.(tan10°-
11.(tan10°-![]() )sin40°=________
)sin40°=________
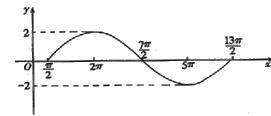
12.函数y=Asin(ωx+φ)![]() 部分图象
部分图象
如图,则函数解析式为y= .
 |
13.某工厂2005年的年生产总值为200万元,
技术革新后预计以后每年的年生产总值都比
上一年增长5%.为了求年生产总值超过300
万元的最早年份,有人设计了解决此问题的
程序框图(如右图),请在空白判断框内填
上一个适当的式子.
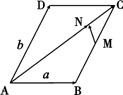 14.在平行四边形ABCD中,
14.在平行四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,
M为BC的中点,则![]() _________.(用
_________.(用![]() ,
,![]() 表示)
表示)
 三. 解答题:本大题共5小题,共44分.解答应写出文字说明,证明过程或演算步骤.
三. 解答题:本大题共5小题,共44分.解答应写出文字说明,证明过程或演算步骤.
15、(本小题满分9分)
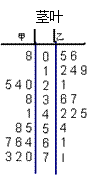
为了调查甲、乙两个交通站的车流量,随机选取了14天,
统计每天上午8:00—12:00间各自的车流量(单位:百辆),
得如下所示的统计图,根据统计图:
(1)甲、乙两个交通站的车流量的极差分别是多少?
(2)甲交通站的车流量在[10,40]间的频率是多少?
(3)甲、乙两个交通站哪个站更繁忙?并说明理由.
16、(本小题满分9分)
已知矩形ABCD中,![]() ,
,![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .
.
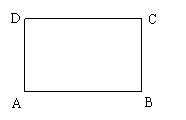 (1)若
(1)若![]() ,求
,求![]() 、
、![]() 的值;
的值;
(2)求![]() 与
与![]() 的夹角的余弦值.
的夹角的余弦值.
17、(本小题满分9分)
甲袋内装有大小相同的1只白球,2只红球,3只黑球;乙袋内装有大小相同的2只白球,3只红球,1只黑球,现从两袋中各取一球,求两球同色的概率.
18、(本小题满分9分)
已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,求
,求![]() 的值.
的值.
19、(本小题满分8分)
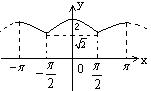
函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等,请选择适当的探究顺序研究函数f(x)=![]() 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在![]() 上的图象.
上的图象.
数学科试卷答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | C | C | B | A | C | D | B | C | D |
二、填空题
11.-1
12.![]()
13.![]() ?
?
14.![]()
三、解答题
15.解:(1)甲交通站的车流量的极差为:73-8=65,
乙交通站的车流量的极差为:71-5=66.
(2)甲交通站的车流量在[10,40]间的频率为![]() .
.
(3)甲交通站的车流量集中在茎叶图的下方,而乙交通站的车流量集中在茎叶图的上方.从数据的分布情况来看,甲交通站更繁忙.
16.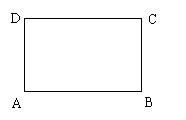 解:(1)
解:(1)![]()
![]() ,
,![]()
![]()
![]() =4
=4![]() +3
+3![]()
![]()
![]() ,
,![]()
(2)由![]() =3
=3![]() -4
-4![]() ,设
,设![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则
![]() ,
,![]()
![]()
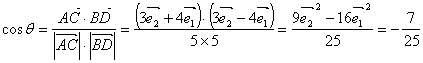
![]()
![]() 与
与![]() 的夹角的余弦值为
的夹角的余弦值为![]() .
.
17.解法一:设甲袋内1只白球用A表示,2只红球用![]() 、
、![]() 表示,3只黑球用
表示,3只黑球用![]() 、
、![]() 、
、![]() 表示;乙袋内2只白球用
表示;乙袋内2只白球用![]() 、
、![]() 表示,3只红球用
表示,3只红球用![]() 、
、![]() 、
、![]() 表示,1只黑球用
表示,1只黑球用![]() 表示。则从两袋中各取一球的基本事件总数为6×6=36。
表示。则从两袋中各取一球的基本事件总数为6×6=36。
其中同色的有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共11个基本事件。
共11个基本事件。
∴从两袋中各取一球,其中两球同色的概率P=![]() 。
。
解法二:设甲袋内1只白球用A表示,2只红球用![]() 、
、![]() 表示,3只黑球用
表示,3只黑球用![]() 、
、![]() 、
、![]() 表示;乙袋内2只白球用
表示;乙袋内2只白球用![]() 、
、![]() 表示,3只红球用
表示,3只红球用![]() 、
、![]() 、
、![]() 表示,1只黑球用
表示,1只黑球用![]() 表示。则从两袋中各取一球的基本事件总数为6×6=36。
表示。则从两袋中各取一球的基本事件总数为6×6=36。
其中,从两袋中各取一球均为白球的事件数为1×2=2,从两袋中各取一球均为红球的事件数为2×3=6,从两袋中各取一球均为黑球的事件数为3×1=3。
∴两球同色的概率P=![]()
18.解:![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
由![]() ,得
,得![]() ,即
,即![]()
![]()
![]()
又由![]() ,得
,得![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() =
=![]()
19、解:①
∵![]() ∴
∴![]() 的定义域为
的定义域为![]()
② ∵![]()
∴f(x)为偶函数;
③ ∵f(x+![]() )=f(x), ∴f(x)是周期为
)=f(x), ∴f(x)是周期为![]() 的周期函数;
的周期函数;
④ ∵![]()
∴当![]() 时
时![]() ;当
;当![]() 时
时![]()
(或当![]() 时f(x)=
时f(x)=![]()
∴当![]() 时
时![]() 单减;当
单减;当![]() 时
时![]() 单增; 又∵
单增; 又∵![]() 是周期为
是周期为![]() 的偶函数
的偶函数
∴f(x)的单调性为:在![]() 上单增,在
上单增,在![]() 上单减.
上单减.
⑤ ∵当![]() 时
时![]() ;当
;当![]() 时
时![]()
∴![]() 的值域为:
的值域为:![]()
⑥由以上性质可得:![]() 在
在![]() 上的图象如上图所示:
上的图象如上图所示:
注:以下各题来源于教材:
第1题:必修4,P10-5(2)
第2题:必修4,P25-例1(3)
第5题:必修4,P140-例3
第6题:必修4,P120-1(6)
第11题:必修4,P146-5(2)
第13题:必修3,P15-例7
第17题:必修3,P139-例3