高一数学第二学期期末考试试题
2008年6月
(考试时间120分钟,试卷满分150分)
第Ⅰ卷
一、选择题(本大题共12小题,每小题5分,共60分.在每一小题的四个选项中,只有一项是符合题目要求的)
1.下列命题中正确的是
A.第一象限角一定不是负角
B.小于![]() 的角一定是锐角
的角一定是锐角
C.钝角一定是第二象限角 D.终边相同的角一定相等
2.若![]() ,且
,且![]() ,则
,则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
3.在平行四边形![]() 中,若
中,若![]() ,则必有
,则必有
A.![]() 是菱形
B.
是菱形
B.![]() 是矩形
是矩形
C.![]() 是正方形
D.以上都错
是正方形
D.以上都错
4.若![]() 为第二象限角,则
为第二象限角,则![]()
A.1 B.0 C.2 D.-2
5.不等式![]() 的解集是
的解集是![]() ,则
,则![]() 等于
等于
A.-10 B.10 C.14 D.-4
6.设![]() ,把
,把![]() 的图像按向量
的图像按向量![]() 平移后,图像恰好为函数
平移后,图像恰好为函数![]() 的图像,则
的图像,则![]() 的值可以为
的值可以为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在![]() 中,若
中,若![]() ,则
,则![]() 一定为
一定为
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形
8.函数![]() 的图象
的图象
A.关于原点对称; B.关于点![]() 对称; C.关于
对称; C.关于![]() 轴对称;D.关于直线
轴对称;D.关于直线![]() 对称.
对称.
9.在![]() 中,
中,![]() ,那么
,那么![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知![]() 、
、![]() 以及
以及![]() 均为锐角,
均为锐角,![]() ,
,![]() ,
,![]() ,那么
,那么![]() 、
、![]() 、
、![]() 的大小关系是
的大小关系是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知向量![]() ,其中
,其中![]() 、
、![]() 均为非零向量,则
均为非零向量,则![]() 的取值范围是
的取值范围是
A. [0,![]() ] B.[0,1]
C.(0,2)
D.[0,2]
] B.[0,1]
C.(0,2)
D.[0,2]
12.点![]() 是
是![]() 所在平面内一点,满足
所在平面内一点,满足![]() ,则点
,则点![]() 是
是![]() 的
的
A.内心 B.外心 C.重心 D.垂心
第二学期期末考试
高 一 数 学 试 题 2008年6月
(考试时间120分钟,试卷满分150分)
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
第Ⅱ卷
一、选择题(本大题共12小题,每小题5分,共60分.在每一小题的四个选项中,只有一项是符合题目要求的.将正确答案填写在下表中)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(本大题共4小题,每小题4分,共16分.答案填写在题中横线上)
13.若实数![]() 、
、![]() 满足
满足![]() ,则
,则![]() 的最小值是__________.
的最小值是__________.
14.已知![]() ,则
,则![]() __________.
__________.
15.函数![]() 的值域是__________.
的值域是__________.
16.在![]() 中,
中,![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 的值为 .
的值为 .
三、解答题(本大题共6小题,满分74分)
17. (本大题满分12分)
已知![]() ,
,![]() ,
,
(Ⅰ)若![]() 、
、![]() 的夹角为
的夹角为![]() ,求
,求![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 与
与![]() 的夹角.
的夹角.
18.(本大题满分12分)
已知![]() ,求证
,求证![]() .
.
19. (本大题满分12分)
设![]() ,解关于
,解关于![]() 的不等式
的不等式![]()
 20.
(本大题满分12分)
20.
(本大题满分12分)
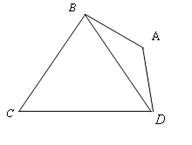
![]() 如图,在平面四边形
如图,在平面四边形![]() 中,
中,![]() 是正三角形,
是正三角形,
![]() ,
,![]() .
.
(Ⅰ)将四边形![]() 的面积
的面积![]() 表示成关于
表示成关于![]() 的函数;
的函数;
(Ⅱ)求![]() 的最大值及此时
的最大值及此时![]() 的值.
的值.
21.(本大题满分12分)
已知向量![]()
![]() ,
,![]()
![]() ,其中
,其中![]() ,设函数
,设函数![]() .
.
(Ⅰ)若函数![]() 的周期是
的周期是![]() ,求函数
,求函数![]() 的单调增区间;
的单调增区间;
(Ⅱ)若函数![]() 的图象的一条对称轴为
的图象的一条对称轴为![]() ,求
,求![]() 的值.
的值.
22.(本大题满分14分)
在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 三点满足
三点满足![]() .
.
(Ⅰ)求证:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(Ⅱ)求![]() 的值;
的值;
(Ⅲ)已知![]() 、
、![]() ,
,
![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值.
的值.
赣州市2007~2008学年度第二学期期末考试
高一数学试题参考答案及评分标准 2008年6月
一、选择题
1~5 CDBCA;6~10 DAB AC; 11~12.DD
二、填空题
13.6;14.![]() ;15.
;15.![]() ;16.
;16.![]() .
.
三、解答题
17.解:(Ⅰ)∵![]() …………………………………………………………1分
…………………………………………………………1分
![]() …………………………………………………………4分
…………………………………………………………4分
∴![]()
![]() ……………………………………………………………6分
……………………………………………………………6分
(Ⅱ)∵![]() ……………………………………………………………7分
……………………………………………………………7分
∴![]() …………………………………………………………………9分
…………………………………………………………………9分
故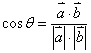 …………………………………………………………10分
…………………………………………………………10分
![]() ……………………………………………………………12分
……………………………………………………………12分
18.证明:要证![]() ………………………………………………………1分
………………………………………………………1分
即证![]() …………………………………………………3分
…………………………………………………3分
即证![]() …………………………………………………5分
…………………………………………………5分
若![]() ,上式显然成立……………………………………………………6分
,上式显然成立……………………………………………………6分
若![]() 则只要证
则只要证![]() ………………………7分
………………………7分
即证![]() ………………………………………………………………9分
………………………………………………………………9分
即![]() …………………………………………………………………10分
…………………………………………………………………10分
∵![]() ,∴
,∴![]() 成立…………………………………………………11分
成立…………………………………………………11分
故![]() 成立……………………………………………………12分
成立……………………………………………………12分
证法二:![]() …………………………………1分
…………………………………1分
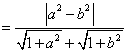 …………………………………………………3分
…………………………………………………3分
![]() …………………………………………5分
…………………………………………5分
![]() ……………………………………………87分
……………………………………………87分
![]() …………………………………………………………10分
…………………………………………………………10分
![]() ………………………………………………………………11分
………………………………………………………………11分
∴![]() ……………………………………………12分
……………………………………………12分
19.解:原不等式化为:![]() …………………………………………3分
…………………………………………3分
即:![]() ……………………………………………………6分
……………………………………………………6分
①当![]() 时,解集为
时,解集为![]() ………………………………………8分
………………………………………8分
②当![]() 时,解集为
时,解集为![]() …………………………………………10分
…………………………………………10分
③当![]() 时,解集为
时,解集为![]() …………………………………………12分
…………………………………………12分
20.解:(Ⅰ)![]() 的面积
的面积![]() …………………………2分
…………………………2分
![]() 中,
中,![]() …………………4分
…………………4分
∵![]() 是正三角形.
是正三角形.
∴ ![]() 的面积
的面积![]() …………6分
…………6分
∴![]() ………………………………………………7分
………………………………………………7分
![]() ………………………………………8分
………………………………………8分
∴![]() …………………………………………9分
…………………………………………9分
(Ⅱ)当![]() ,即
,即![]() 时……………………………………………11分
时……………………………………………11分
![]() 取得最大值
取得最大值![]() ………………………………………………………………12分
………………………………………………………………12分
21.解:(Ⅰ)![]()
![]()
![]() …1分
…1分
![]() …………………………………………………2分
…………………………………………………2分
∵ 周期![]() ,∴
,∴![]() ,又
,又![]() ,故
,故![]() ……………………4分
……………………4分
![]() …………………………………………………………5分
…………………………………………………………5分
令![]()
![]() ……………6分
……………6分
∴函数![]() 的单调增区间为
的单调增区间为![]()
![]() ……………………8分
……………………8分
(Ⅱ)函数![]() 的图象的一条对称轴为
的图象的一条对称轴为![]()
∴![]() ………………………………………10分
………………………………………10分
又![]() ,∴
,∴![]() …………………………………………………12分
…………………………………………………12分
22.解:(Ⅰ)由已知得![]() ……………………………………………1分
……………………………………………1分
即![]() ………………………………………………………………………2分
………………………………………………………………………2分
∴![]() ∥
∥![]() ……………………………………………………………………………3分
……………………………………………………………………………3分
又∵![]() 、
、![]() 有公共点
有公共点![]()
∴![]() 、
、![]() 、
、![]() 三点共线…………………………………………………………………4分
三点共线…………………………………………………………………4分
(Ⅱ) ∵![]()
∴![]() ……………………………………………………………………5分
……………………………………………………………………5分
∴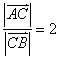 …………………………………………………………………………6分
…………………………………………………………………………6分
(Ⅲ)∵![]() 分
分![]() 的比
的比![]() …………………………………………………………7分
…………………………………………………………7分
∴![]() ………………………………………………………8分
………………………………………………………8分
∵![]() ,∴
,∴![]()
![]() …………………………………9分
…………………………………9分
![]() ……………………………………………………10分
……………………………………………………10分
∵![]() ,∴
,∴![]()
①当![]() ,当且仅当
,当且仅当![]() 时,
时,
![]() 取得最小值为1(舍去)……………………………………………11分
取得最小值为1(舍去)……………………………………………11分
②当![]() 时,当且仅当
时,当且仅当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() ,
,
![]() (舍去)……………………………………………………12分
(舍去)……………………………………………………12分
③当![]() 时,当且仅当
时,当且仅当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() ,
,
![]() ………………………………………………13分
………………………………………………13分
综上![]() ……………………………………………………………14分
……………………………………………………………14分