高一数学圆锥曲线方程练习卷
一选择题:
1、
到两定点![]() 和
和![]() 的距离之和为4的点M的轨迹是:( )
的距离之和为4的点M的轨迹是:( )
A、椭圆 B、线段 C 、圆 D、以上都不对
2、椭圆![]() 上一点P到一焦点距离为7,则P到另一焦点距离为:( )
上一点P到一焦点距离为7,则P到另一焦点距离为:( )
A、3 B、5 C、1 D、7
3、若椭圆两准线间的距离等于焦距的4倍,则此椭圆的离心率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、已知方程![]() 表示双曲线,则
表示双曲线,则![]() 的取值范围是:( )
的取值范围是:( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、双曲线![]() 的左、右焦点分别为F1,F2,在左支上过点F1的弦AB的长为5,那么△ABF2的周长是( )
的左、右焦点分别为F1,F2,在左支上过点F1的弦AB的长为5,那么△ABF2的周长是( )
A、16 B、18 C、21 D、26
6、双曲线与椭圆![]() 有相同的焦点,它的一条渐近线为
有相同的焦点,它的一条渐近线为![]() ,则双曲线方程为:( )
,则双曲线方程为:( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、与圆![]() 外切又和Y轴相切的圆的圆心轨迹方程是:( )
外切又和Y轴相切的圆的圆心轨迹方程是:( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
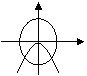

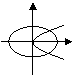
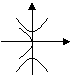 8、方程
8、方程![]() 与
与![]() 在同一坐标系中的大致图象是( )
在同一坐标系中的大致图象是( )
A、 B、 C、 D、
9、抛物线![]() 中,以
中,以![]() 为中点的弦所在直线的方程为:( )
为中点的弦所在直线的方程为:( )
A、
![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、直线![]() 与抛物线
与抛物线![]() 交于A、B两点,O为坐标原点,且
交于A、B两点,O为坐标原点,且![]() 则
则![]() 的值为( )
的值为( )
A、2 B、-2 C、1 D、-1
11、若点A的坐标为(3,2),F为抛物线![]() 的焦点,点P在该抛物线上移动,为使
的焦点,点P在该抛物线上移动,为使![]() 取得最小值,点P的坐标应为( )。
取得最小值,点P的坐标应为( )。
A、(0,0) B 、(1,1) C、(2,2) D、(0.5,1)
12 、椭圆![]() 与直线
与直线![]() 相交于A,B两点,过原点和线段AB中点的直线斜率为
相交于A,B两点,过原点和线段AB中点的直线斜率为![]() ,则
,则![]() 的值是( )
的值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在横线上。
13、点![]() 在椭圆
在椭圆 上则
上则![]() 的最小值为____________。
的最小值为____________。
14、抛物线![]() 按向量平移
按向量平移![]() 后,其顶点在一次函数
后,其顶点在一次函数![]() 的图象上,则
的图象上,则![]() 的值为: _______。
的值为: _______。
15、双曲线![]() 的左焦点到渐近线的距离为________。
的左焦点到渐近线的距离为________。
16、方程![]() 表示曲线C,给出以下命题:①曲线C不可能是圆。
表示曲线C,给出以下命题:①曲线C不可能是圆。
②若曲线C为椭圆,则有1<t<4。
③若曲线C为双曲线,则t<1或t>4
④若曲线C为焦点在X轴上的椭圆,则1<t<2.5
其中正确的是_________________________。
三、解答题:本大题共6小题共48分。解答应写出文字说明,证明过程或演算步骤。
17求下列曲线的的标准方程:
(1)
离心率![]() 且椭圆经过
且椭圆经过![]()
(2)
渐近线方程是![]() ,经过点
,经过点![]() 。
。
18已知一个动圆与圆C:![]() 相内切,且过点A(4,0),求这个动圆圆心的轨迹方程。
相内切,且过点A(4,0),求这个动圆圆心的轨迹方程。
19、已知![]()
20、![]() -1的直线与抛物线
-1的直线与抛物线![]() 交于两点A,B,如果
交于两点A,B,如果![]() (O为原点)求P的值及抛物线的焦点坐标。
(O为原点)求P的值及抛物线的焦点坐标。
21、P为椭圆![]() 上一点,左、右焦点分别为F1,F2。
上一点,左、右焦点分别为F1,F2。
(1) 若PF1的中点为M,求证![]()
(2) 若![]() ,求
,求![]() 之值。
之值。
(3) 求 ![]() 的最值。
的最值。
22、已知椭圆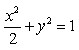 ,
,
(1)求斜率为2的平行线的中点轨迹方程。
(2)过A(2,1)的直线L与椭圆相交,求L被截得的弦的中点轨迹方程;
(3)过点P(0.5,0.5)且被P点平分的弦所在直线的方程。