高一下学期期末考试数学模拟练习四
沈阳市同泽高级中学高一数学组 谷凤军 2008年7月2日
一、选择题
1.若![]() 是锐角,且满足
是锐角,且满足![]() ,则
,则![]() 的值为
的值为
A ![]() B
B ![]() C
C ![]() D
D ![]()
2.在120个零件中,一级品24个,二级品36个,三级品60个,用分层抽样法从中抽取容量为20的样本,则应抽取三级品的个数为
A 2 B 4 C 6 D 10
3.从分别写上数字1,2,3……9的9张卡片中,任意取出两张,观察上面的数字,则两数积是完全平方数的概率为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
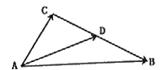
4.已知![]() 为平面上不共线的三点,若向量
为平面上不共线的三点,若向量![]() =(1,1),
=(1,1),![]() =(1,-1),且
=(1,-1),且![]() ·
·![]() =2,则
=2,则![]() ·
·![]() 等于
等于
A -2 B 2 C 0 D 2或-2
5.函数![]() ,那么任取点
,那么任取点![]() ,使
,使![]() 的概率为
的概率为
A.
0.1
B. ![]() C.0.3
D. 0.4
C.0.3
D. 0.4
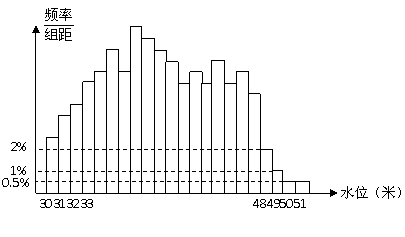
6.根据某水文观测点的历史统计数据,得到某条河流水位的频率分布直方图如下.从图中可以看出,该水文观测点平均至少一百年才遇到一次的洪水的最低水位是
A.48米 B.49米 C.50米 D.51米

7.若函数![]() 在区间[
在区间[![]() ]上单调递增,则函数
]上单调递增,则函数![]() 的表达式为
的表达式为
A ![]() B -
B - ![]() C 1
D -
C 1
D -![]()
8.一个袋中装有2个红球和2个白球,现从袋中取出1球,然后放回袋中再取出一球,则取出的两个球同色的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9.有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有”20”,”08”和”北京”的字块,如果婴儿能够排成”2008北京”或者”北京2008”,则他们就给婴儿奖励.假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.函数![]() 是奇函数,则
是奇函数,则![]() 等于
等于
A ![]() B -
B - ![]() C
C ![]() D -
D - ![]()
11.已知![]() 为原点,点
为原点,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() 其中常数
其中常数![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() =
=![]()
![]() (
(![]() ),则
),则![]() ·
·![]() 的最大值为
的最大值为
A ![]() B 2
B 2![]() C 3
C 3![]() D
D ![]()
|
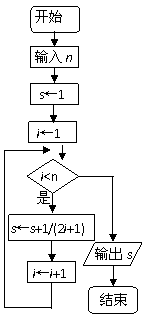 A.
A.![]() B.
B.![]() C.7 D.18
C.7 D.18
二、填空题
13.已知│![]() │=│
│=│![]() │=2,
│=2, ![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() +
+![]() 在
在![]() 上的正射影的数量为_____________.
上的正射影的数量为_____________.
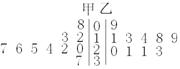 14.某篮球学校的甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下.则罚球命中率较高的是_______.
14.某篮球学校的甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下.则罚球命中率较高的是_______.
15.右图中所示的S的表达式为 ____________
16.设函数![]() ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线![]() 对称;
对称;
②它的图象关于点(![]() ,0)对称;
,0)对称;
③它的最小正周期是![]() ;
;
④在区间[![]() ]上是增函数.
]上是增函数.
以其中两个论断作为条件,余下论断作为结论,写出一个正确的命题:
条件_____________,结论____________.
选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
三、解答题
17.已知向量![]() 满足
满足![]() ,且
,且![]() 。
。
(1)、求向量![]() 的坐标; (2)、求向量
的坐标; (2)、求向量![]() 与
与![]() 的夹角。
的夹角。
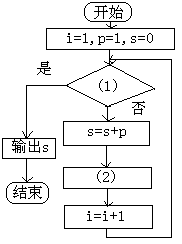
18.给出30个数:1,2,4,7,……,其规律是:第1个数是1,第2个数比第1个数大1, 第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的流程图(如图所示),(I)请在图中判断框内(1)处和执行框中的(2)处填上合适的语句,使之能完成该题算法功能
19.在锐角三角形![]() 中,
中,![]() ,求
,求![]() 的值.
的值.
20.一个口袋内装有形状、大小都相同的2个白球和3个黑球.
(1)从中一次随机摸出两个球,求两球恰好颜色不同的概率;
(2)从中随机摸出一个球,不放回后再随机摸出一个球,求两球同时是黑球的概率;
(3)从中随机摸出一个球,放回后再随机摸出一个球,求两球恰好颜色不同的概率.
21.已知![]() 为
为![]() 的外心,以线段
的外心,以线段![]() 为邻边作平行四边形,第四个顶点为
为邻边作平行四边形,第四个顶点为
![]() ,再以
,再以![]() 为邻边作平行四边形,它的第四个顶点为
为邻边作平行四边形,它的第四个顶点为![]() .
.
(1) 若![]() ,试用
,试用![]() 表示
表示![]() ;
;
(2)证明:![]() ;
;
(3)若![]() 的
的![]() 外接圆的半径为
外接圆的半径为![]() ,用
,用![]() 表示
表示![]() .
.
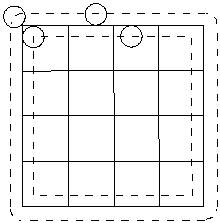
|
(1)求硬币落下后完全在最大的正方形内的概率;
(2)求硬币落下后与网格线没有公共点的概率.
三参考答案
BDABC BBA CD DA
13. 3 14. 甲 15.![]() 16.②③
16.②③![]() ①④或①③
①④或①③![]() ②④
②④
17. 解:(1)![]() 因为
因为
![]() 则
则 ![]() -------①
-------①
又∵ 已知![]() ,且
,且![]()
![]()
∴ ![]() -------②
-------②
由①②解得 ![]() ∴
∴![]()
(2)设向量![]() 与
与![]() 的夹角
的夹角![]() ∵
∵![]() -
-
∴ 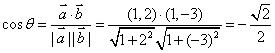 -
-
或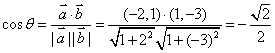
∵![]() ∴向量
∴向量![]() 与
与![]() 的夹角
的夹角![]()
18.
19. 解:因为A+B+C=![]() ,所以
,所以![]() ,又有
,又有![]() ,A为锐角得cosA=
,A为锐角得cosA=![]()
所以![]()
=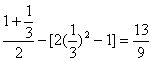
20. 解:(1)记“一次摸出两个球,两球颜色恰好颜色不同”为事件A,
摸出两个球的基本事件共有10种,其中两球为一白一黑的事件有6种.
![]() .
.
答:从中一次摸出两个球,求两球恰好颜色不同的概率是0.6.
(2)记“从中摸出一个球,不放回后再摸出一个球,两球同时是黑球”为事件B,
不放回地摸出两个球的基本事件共有20种,其中两球为黑球的事件有6种.
![]() .
.
答:从中摸出一个球,不放回后再摸出一个球,求两球为黑球的概率是![]() .
.
(3)记“从中摸出一个球,放回后再摸出一个球,两球颜色恰好颜色不同”为事件C,
有放回地摸出两个球的基本事件共有25种,其中两球为一白一黑的事件有12种.
![]() .
.
答:从中摸出一个球,放回后再摸出一个球,求两球恰好颜色不同的概率是0.48.
21. 解:(1)由平行四边形法则可得:![]()
即![]()
(2)![]() O是
O是![]() 的外心,
的外心,![]() ∣
∣![]() ∣=∣
∣=∣![]() ∣=∣
∣=∣![]() ∣,
∣,
即∣![]() ∣=∣
∣=∣![]() ∣=∣
∣=∣![]() ∣,而
∣,而![]() ,
,
![]()
![]()
![]()
![]() =∣
=∣![]() ∣-∣
∣-∣![]() ∣=0,
∣=0,![]()
![]()
(3)在![]() 中,O是外心A=
中,O是外心A=![]() ,B=
,B=![]()
![]()
![]()
于是![]() ∣
∣![]() ∣2=(
∣2=(![]()
=![]() +2
+2![]() +2
+2![]() =(
=(![]() )
)![]() ,
,
![]()
![]()
22. 解:考虑圆心的运动情况.
(1)因为每次投掷都落在最大的正方形内或与最大的正方形有公共点,所以圆心的最大限度
为原正方形向外再扩张1个小圆半径的区域,且四角为四分之圆弧;此时总面积为:
16×16+4×16×1+π×12=320+π;完全落在最大的正方形内时,圆心的位置
在14为边长的正方形内,其面积为:14×14=196;
故:硬币落下后完全在最大的正方形内的概率为:![]() ;
;
(2)每个小正方形内与网格线没有公共点的部分是正中心的边长为2的正方形的内部,一共有16个小正方形,总面积有:16×22=64;
故:硬币落下后与网格线没有公共点的概率为:![]() .
.
答:硬币落下后完全在最大的正方形内的概率为:![]() ;
;
硬币落下后与网格线没有公共点的概率为:![]() .
.