高一下期末综合数学试题(五)
(考试时间:120分钟 满分150分)
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在△ABC中,![]() ,则∠C为
(
)
,则∠C为
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
2. 下列不等式中不一定成立的是 ( )
A.![]() >0时,
>0时,![]()
![]() 2
2![]() B.
B.![]()
![]() 2
2
C.![]()
![]() 2
D.
2
D.![]() >0时,
>0时,![]()
![]() 4
4
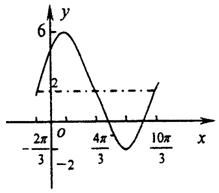
3.函数![]() 的单调减区间为
( )
的单调减区间为
( )
A ![]()
![]() B
B ![]()
![]()
C ![]()
![]() D。
D。![]()
4.若函数![]() 的图象按向量
的图象按向量![]() 平移后,得到的图象关于原点对称,则向量
平移后,得到的图象关于原点对称,则向量![]() 可以是:
( )
可以是:
( )
A.![]() B.(
B.(![]() C.
C.![]() D.
D.![]()
5.已知![]() +
+![]() +
+![]() =
=![]() ,
,![]() =2,
=2,![]() =3,
=3,![]() =
=![]() ,则向量
,则向量![]() 与
与![]() 之间的夹角
之间的夹角![]() 为 ( )
为 ( )
A.30° B.45° C.60° D.以上都不对
6.甲、乙两厂2006年元月份的产值相等,甲厂的产值逐月增加且每月增加的产值相同,乙厂的产值也逐月增加且每月增加的百分率相同;已知2007年元月份两厂的产值相同,则2007年7月份产值高的工厂是 ( )
A.甲厂 B.乙厂 C.两厂一样 D.无法确定
7.设直角三角形两直角边的长分别为a和b,斜边长为c,斜边上的高为h,则![]() 的大小关系是
( )
的大小关系是
( )
A、![]() B、
B、![]() C、
C、![]() D、无法确定
D、无法确定
8.在![]() 上定义运算
上定义运算![]() :
:![]()
![]()
![]() .若不等式
.若不等式![]()
![]()
![]() 对任意实数
对任意实数![]() 恒成立,则
恒成立,则![]() 的取值区间是
(
)
的取值区间是
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.在△ABC中,![]() ,若△ABC的最长边为
,若△ABC的最长边为![]() ,则最短边的长为 ( )
,则最短边的长为 ( )
|
|
A.![]()
B.![]()
C.![]()
D.![]()
11、△ABC中,![]() =5,
=5,![]() =8,
=8,![]() ·
·![]() =20,则
=20,则![]() 为
(
)
为
(
)
A. 6 B. 7 C. 8 D. 9
12.设![]() ,已知两个向量
,已知两个向量![]() ,
,![]() ,则向量
,则向量![]() 长度的最大值是
( )
长度的最大值是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共5小题,每小题4分,共20分)
13.方程x2-2ax+a+![]() =0,有二实根α、β,则(α-1)2+(β-1)2的最小值为 。
=0,有二实根α、β,则(α-1)2+(β-1)2的最小值为 。
14.函数f(x)=![]() 的值域为
的值域为![]() 。
。
15.不等式![]() 的解集是
的解集是![]() 。
。
16.已知![]() ,
,![]() 的夹角为
的夹角为![]() ,则
,则![]() 在
在![]() 上的投影为______ ________;
上的投影为______ ________;
17.下列命题中正确的序号为![]() (你认为正确的都写出来)
(你认为正确的都写出来)
①![]() 的周期为
的周期为![]() ,最大值为
,最大值为![]() ; ②若x是第一象限的角,则
; ②若x是第一象限的角,则![]() 是增函数;
是增函数;
③在![]() 中若
中若![]() 则
则![]() ; ④
; ④![]() 且
且![]()
⑤![]() 既不是奇函数,也不是偶函数;
既不是奇函数,也不是偶函数;
三、解答题(本大题共6小题,共70分)
18.(本小题10分)已知向量![]()
求函数![]() 的最大值、最小正周期,并写出
的最大值、最小正周期,并写出![]() 在
在![]() 上的单调区间。
上的单调区间。
19. (本小题12分)已知A、B、C坐标分别为![]() ,
,![]()
(1) 若![]() ,求角
,求角![]() 的值;
的值;
(2) 若![]() ,求
,求![]() 的值。
的值。
20.(本小题12分) 如图,在△ABC中,点M为BC的中点,A、B、C三点坐标分别为(2,-2)、(5,2)、(-3,0),点N在AC上,且![]() ,AM与BN的交点为P,求:
,AM与BN的交点为P,求:
(1)点P分向量![]() 所成的比
所成的比![]() 的值;
的值;
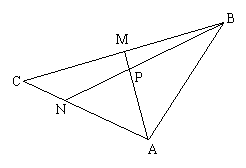 (2)P点坐标.
(2)P点坐标.
21.(本小题12分)已知△ABC的周长为6,![]() 成等比数列,求
成等比数列,求
(I)试求![]() B的取值范围;
B的取值范围;
(Ⅱ)求![]() 的取值范围.
的取值范围.
22.(本小题12分)、某外商到一开发区投资72万元建起一座蔬菜加工厂,第一年需各种经费为12万元,从第二年开始每年所需经费均比上一年增加4万元,该加工厂每年销售蔬菜总收入为50万元.
(I)若扣除投资及各种经费,该加工厂从第几年开始纯利润为正?
(II)若干年后,外商为开发新项目,对加工厂有两种处理方案:
(1)若年平均纯利润达到最大值时,便以48万元的价格出售该厂;
(2)若纯利润总和达到最大值时,便以16万元的价格出售该厂.
问:哪一种方案比较合算?请说明理由.
23.(本小题12分)设![]() ,
,![]() ,其中
,其中![]() ,且
,且![]()
(1)求证:![]() ;(2)求证:函数
;(2)求证:函数![]() 与
与![]() 的图象有两个不同的交点
的图象有两个不同的交点
(3)设![]() 与
与![]() 图象的两个不同交点为
图象的两个不同交点为![]() 、
、![]() ,求证:
,求证:![]()
宽城一中2007--2008高一下期末综合数学试题(五)参考答案
一、选择题:CCBCC BBCDD BC
二、填空题:13、![]() 14、
14、![]() 15、
15、![]()
16、3 17、①③④⑤
三、解答题: 18、解:![]()
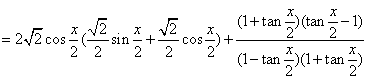
![]()
所以![]() 的最大值为
的最大值为![]() ,最小正周期
,最小正周期![]() ,在
,在![]() 上递增,在
上递增,在![]() 上递减。
上递减。
19.解:(1)![]() .
.
![]() ,
,
![]() ,
,
∵![]() ,
,![]() ,
4分
,
4分
又 ![]()
![]() …..6分
…..6分
(2)由![]() 知:
知:![]() 。
。
![]() , ∴
, ∴![]()
∴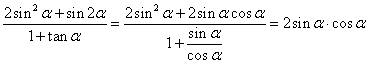 =
=![]() 12分
12分
20.解:(1)∵A、B、C三点坐标分别为![]() 、
、![]() 、
、![]()
由于M为BC中点,可得M点的坐标为(1,1) ……2分
由![]() 可得N点的坐标为
可得N点的坐标为![]() ……4分
……4分
又由![]() 可得P点的坐标为(
可得P点的坐标为(![]() ,
,![]()
从而得![]() ,
,![]()
![]() ,
,![]()
∵![]() 与
与![]() 共线 故有
共线 故有![]() )
)![]()
![]() )-(
)-(![]()
![]() (
(![]() =0 解之得
=0 解之得![]() 4 …8分
4 …8分
∴点P的坐标为(![]() ,
,![]() )
……12分
)
……12分
21.解:(1)设![]() 依次为
依次为![]() ,则
,则![]() ,
,
由余弦定理得![]() 故有
故有![]() ,…6分
,…6分
(2) 又![]() 从而
从而![]()
所以 ![]()
![]() …10分
…10分
![]() ……12分
……12分
22.解:由题设知,每年的经费是以12为首项,4为公差的等差数列
设纯利润与年数的关系为![]() ,
,
则![]()
(I)获纯利润就是要求![]() ,
,![]()
即![]() ,
,
![]() ,
,
![]() 从第3年开始获利.
…………………………………………6/
从第3年开始获利.
…………………………………………6/
(II)(1)年平均纯利润![]() ,
,
![]() ,当且仅当
,当且仅当![]() 时,取“=”号,
时,取“=”号,
![]() ,
,
![]() 第(1)种方案共获利
第(1)种方案共获利![]() (万元),此时
(万元),此时![]() . …………10/
. …………10/
(2)![]() ,
,
当![]() 时,
时,![]() .
.
故第(2)种方案共获利![]() (万元).
…………12/
(万元).
…………12/
比较两种方案,获利都为144万元,但第(1)种方案需6年,而第(2)种方案需10年,
故选择第(1)种方案.
23、解(1)由![]() ,
,![]() 可知
可知![]()
由![]() 得
得![]() 即
即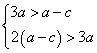 ,
, ![]() 且
且![]() … 4分
… 4分
(2)由![]() 得
得 ![]()
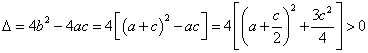
故有两个不同交点 …… 8分
(3)![]()
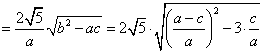
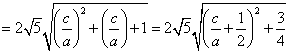
又 ![]() 从而得证
从而得证![]() ……12分
……12分