高二年暑假返校测试数学试卷2008.7
注:1.本卷不能使用计算器;
2.本卷满分100分,考试时间100分钟.
一、选择题(本大题共10小题,每小题4分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1、已知集合M ={ x(x + 2)(x-1) < 0 },N ={ x x + 1 < 0 },则M∩N =( )
A. (-1,1) B. (-2,1) C. (-2,-1) D. (1,2)
2、已知![]() 为
为![]() 的一个内角,向量
的一个内角,向量![]()
![]() .若
.若![]() ,则角
,则角![]() 的大小为( )
的大小为( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
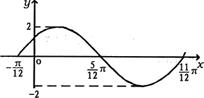
3、已知函数y=2sin(ωx+φ)(ω>0)在某区间的图像如右:
那么ω=( )
A. 1 B. 2 C. 1/2 D. 1/3
4、下列说法正确的是( )
A
.a∥![]() ,b∥
,b∥![]()
![]() a∥b B. 垂直同一平面的两平面平行
a∥b B. 垂直同一平面的两平面平行
C .a∥b,a∥![]()
![]() b∥
b∥![]() D. 垂直同一直线的两平面平行
D. 垂直同一直线的两平面平行
5、空间直角坐标系![]() 中,点
中,点![]() 关于平面
关于平面![]() 的对称点的坐标是( )
的对称点的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、设变量![]() 满足约束条件:
满足约束条件: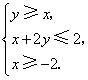 ,则
,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、 直线ax+(1-a)y=3与直线(a-1)x+(2a+3)y=2互相垂直,则a的值为( )
(A)-3 (B) 1 (C) 0或-![]() (D)1或-3
(D)1或-3
8、函数![]() 的图象是( )
的图象是( )
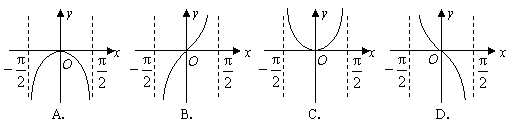
9、下列不等式中不一定成立的是 ( )
(A)![]() >0时,
>0时,![]()
![]() 2
(B)
2
(B)![]()
![]() 2
2
(C)![]()
![]() 2
(D)
2
(D)![]() >0时,
>0时,![]()
![]() 4
4
10、在平面直角坐标中,与点A(1,1)的距离为1,且与点B(-2,-3)的距离为6的直线有( )条。
A.0 B.1 C.2 D.无数条
二、填空题:(本大题共5小题,每小题4分,共20分。)
11.方程![]() 的实数解的个数为
.
的实数解的个数为
.
 12.已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC的中点, 则AM所在的直线方程为
。
12.已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC的中点, 则AM所在的直线方程为
。
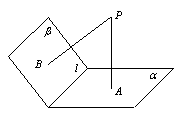
13.如图,已知二面角α - l - β 的大小是120°,PA⊥α,
PB⊥β,则PB与平面α所成的角为 ▲ .
14.把函数![]() 的图象上所有的点向左平行
的图象上所有的点向左平行
移动![]() 个单位长度,再把所得图象上所有点的横坐标缩短到原来的
个单位长度,再把所得图象上所有点的横坐标缩短到原来的![]() 倍(纵坐标不变),得到的图象所表示的函数的单调递减区间是
倍(纵坐标不变),得到的图象所表示的函数的单调递减区间是
15.已知![]() ,则
,则![]() 的值等于
.
的值等于
.
 瓯海中学新高二2008年暑假返校测试
瓯海中学新高二2008年暑假返校测试
![]() 数学答题卷
数学答题卷
一、选择题(本大题共10小题,每小题4分,满分40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(本大题共5小题,每小题4分,共20分)
11. 12.
13. 14.
15.
三、解答题:(本大题共4小题,共40分.解答应写出文字说明、演算步骤或推证过程.)
16.(本题10分) 等差数列![]() 的各项均为正数,
的各项均为正数,![]() ,前
,前![]() 项和为
项和为![]() ,
,![]() 为等比数列,
为等比数列, ![]() ,且
,且![]()
![]() .
.
(1)求![]() 与
与![]() ;
;
(2)求证:![]() .
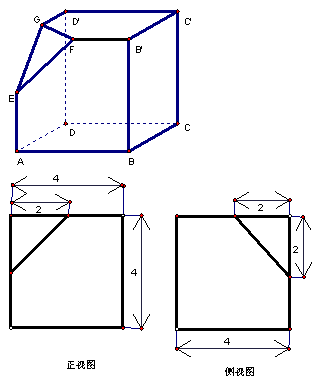
.
17.(本题10分)如下的三个图中,上面的是一个正方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm)。(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积;(3)在所给直观图中连结![]() ,求
,求![]() 与EF所成的角的大小。
与EF所成的角的大小。
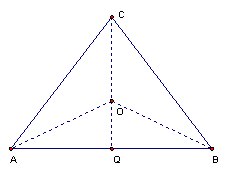
18.(本题10分)如图,某住宅小区有三幢居民楼房,分别位于底边AB=2(百米)的等腰直角三角形的顶点A、B及C处,为了处理三幢居民楼房里生活的污水,现要在三角形ABC的区域内(含边界),且与A、B等距离的一点O处建造一个生活污水处理池,并铺设排污管道AO、BO、OC,设排污管道的总长为y(百米)。
(1)按下列要求写出函数关系式:
①设∠BAO=θ(rad),将y表示成θ的函数关系式;
②设OC=x(百米),将y表示成x的函数关系式;
 (2)请你选用(1)中的一个函数关系式,确定生活污水处理池的位置,使三条排污管道总长度最短。
(2)请你选用(1)中的一个函数关系式,确定生活污水处理池的位置,使三条排污管道总长度最短。
19.(本题10分)已知直线![]() :
:![]() (
(![]() )与圆
)与圆![]() :
:![]() 相交于点
相交于点![]() .
.
(Ⅰ)当k=1时,求弦![]() 的中点
的中点![]() 的坐标;
的坐标;
(Ⅱ)当k变化时,是否存在定点![]() 使得
使得![]() 为定长?若存在,求出定点坐标;若不存在,说明理由.
为定长?若存在,求出定点坐标;若不存在,说明理由.
瓯海中学2007级高二暑期返校考试数学答案(2008.7.30)
一、选择题(本大题共10小题,每小题4分,满分40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | B | D | C | D | D | A | C | B |
二、填空题(本大题共5小题,每小题4分,共20分)
11.2个 12. 2x+y-3=0 13. 30°
14.![]() 15.2008
15.2008
三、解答题:本大题共4小题,共40分.解答应写出文字说明、演算步骤或推证过程
16.(本题10分)
解: (1)设![]() 的公差为
的公差为![]() ,
,![]() 的公比为
的公比为![]() ,则
,则![]() 为正整数,
为正整数,
![]() ,
,![]() ……2分
……2分
依题意有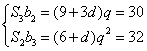 ①
①
解得![]() 或
或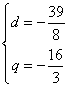 (舍去)
(舍去)
故![]() ……6分
……6分
(2)![]()
∴![]()
![]()
![]()
![]()
![]() ……10分
……10分
17.(本题10分)
解:
(Ⅰ)如图
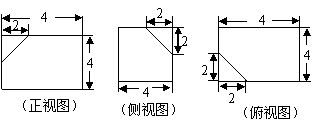

···················································································· 3分
(Ⅱ)所求多面体体积
![]()
![]()
![]() . 6分
. 6分
(Ⅲ) 60° 10分
18.(本题10分)
解:(Ⅰ)①由条件知CO 垂直平分AB,若∠BAO=![]() (rad) ,则
(rad) ,则![]() , 故
, 故
![]() ,又OC=
,又OC=![]() ,
,
所以![]() ,
,
所求函数关系式为![]()
![]() ……3分
……3分
②若OC=![]() (百米) ,则OQ=1-
(百米) ,则OQ=1-![]() ,所以OA
,所以OA
=OB=![]()
所求函数关系式为![]() ………………………………6分
………………………………6分
(Ⅱ)选择函数模型①,记 ![]()
![]() 得
得
![]() ,其中
,其中![]() ,
,![]() ,
,
所以 ![]() 解得
解得![]() 当
当![]() 时,
时,![]() =
=![]() ,
,![]()
所以当![]() =
=![]() 时,
时,![]() (百米)。这时点O 位于线段AB 的中垂线上,在三角形区域内且距离AB 边
(百米)。这时点O 位于线段AB 的中垂线上,在三角形区域内且距离AB 边![]() (百米)处。………………………………10分
(百米)处。………………………………10分
19.(本题10分)
解 (Ⅰ)当![]() 时,
时,
由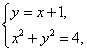 得
得![]()
设![]() ,
,![]() ,则
,则![]() ,
,
![]() .
.
∴![]() . ……………………………… 5分
. ……………………………… 5分
(Ⅱ)存在定点![]() ,使得
,使得![]() 为定长.
为定长.
∵![]() ,直线
,直线![]() :
:![]() (
(![]() )过定点
)过定点![]()
∴点M在以OP为直经的圆周上.
则当T为线段OP的中点时,MT为定长.
∴![]() . ………………………10分
. ………………………10分