高一数学下学期期中试卷
高一 数学
命题人：张思意 审题：段兴仁
[说明]该试卷全卷满分150，考试时间120分钟
一、选择题（本大题共12小题，每小题5分，共60分）
1．点P(cos2070 ,sin2070)在 （ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
2．已知扇形的半径是1，中心角的度数是600.则此扇形的面积是 （ ）
A.、30
B、 
C、 
D、
3．下列等式不成立的是（ ）
A、sin(1800+α)= ―sinα B、cos(900+α)= ―sinα
C、cos (―α)= cosα D、sin(2700-α)=cosα
4．已知x∈（
，0）,cosx=
则tanx的值是（ ）
A、
B、 
C、
D、
―
5．θ是第二象限角，且
=―cos
，则角所在象限是（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
6．已知
＝
，则
＝（ ）
A、 B、 
C、
― D、 ―
7．函数y=sin(―3x+3)的图象可以由函数y=―sin3x的图象经过下列哪个变换得（ ）
A、 向左平移3个单位 B、 向右平移3个单位
C、 向左平移1个单位 D、 向右平移1个单位
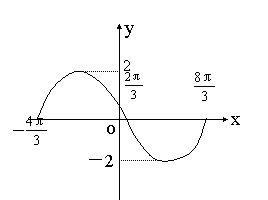
8．函数y＝Asin(ωx＋φ)在一个周期上的图象为右图所示．
则函数的解析式是（ ）
A、y＝2sin(－) B、y＝2sin(＋)
C、y＝2sin(＋) D、y＝2sin(－)
9．已知α,β都是第二象限角,且sinα>sinβ则（ ）
A、 α>β B、 cosα>cosβ C、α<β D、cosα<cosβ
10．使函数f(x)= sin（2x＋θ）＋
cos(2χ＋θ)为奇函数，且在区间[0,
]上为增函数的θ的 一个值为（ ）
A、 B、
C、 D、 
11．已知lg3、lg(sinx―)、lg(2―y)成等差数列。则（ ）
A、
y有最小值
，无最大值 B、 y有最大值2，无最小值
C、 y有最小值
，最大值1 D、 y有最小值－1，最大值1
12．设函数f(x)= 
则函数f(x) （ ）
A、在区间
上递增 B、在区间上递减
C、在区间
上递增，在区间
上递减
D、在区间上递减，在区间上递增
二、填空题（本大题共4小题，每小题4分，共16分）
13．已知sinα+ sinβ＝
，cosα＋cosβ＝
。则cos（α－β）＝
14．设f(x)是定义在R上的函数。满足f(＋x)＝f(x)。且在区间[－,π）上
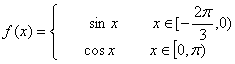则f(－
)＝
15．求值：sin（θ＋780）＋cos(θ+480)－ cos(θ+180)＝
16．设函数y=sin(ωχ＋θ)（ω>0, θ∈（，
）的最小正周期是π，且其图象关于直线x=
对称。则下面四个结论中所有正确结论的编号是
⑴图象关于点（
，0） ⑵图象关于点（
，0）
⑶在[0, ]上是增函数
⑷在[－，0]上是增函数
| 座号 | 总分 |
高一 数学
注：请将选择题、填空题的答案写在答题卷上相应位置
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
一、 选择题（本大题共12小题，每小题5分，共60分）
二、填空题（本大题共4小题，每小题4分，共16分）
13、 . 14、 .
15、 . 16、 .
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）.
17、（本题12分）已知
，求
的值
18、（本题12分）若
，
，且
为锐角,求
的值
19、（本题12分）已知
（a＜0）
（1）求f（x）的最小正周期和单调递增区间；
（2）若
的定义域是
，值域是[―5,1]. 求a、b的值
.
20、（本题12分）设
(A>0,ω>0)函数f(x)的两条相邻的对称轴分别是
直线x=
,直线x=
,且f()－f()＝8
（1）求f(x)的解析式
（2）若角α，β的终边不在同一条直线上且f(α)＝f(β)。求tan(α+β)的值
21．（本题12分）已知
,
（1）把表示成cosx 的函数并求的定义域
（2）当
时，方程 f(x) =
(k∈R)有解，求k的取值范围。
22、（本题14分）已知角
满足方程
。
(A>0,0<ω<2008)且当
时，函数f(x)有最大值2
（1）求实数ω所有可能的值的和
（2）若实数ω取值满足题意的最小值时，不要求画图、说明
的图象是由y=f(x)的图象经过怎样变换得到
（3）、若实数ω取值满足题意的最小值时，函数f（x）与直线y=m在区间
[―，]有两个交点，求实数的取值范围。。