高一数学下学期期中试题
参考公式：锥体的体积公式
，其中
是锥体的底面积，
是锥体的高．
如果事件
互斥，那么
．
用最小二乘法求线性回归方程系数公式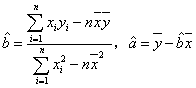
．
一.选择题(共10小题，每小题5分，共50分,在每小题的选项中,只有一项符合题目要求)
1.已知函数
的定义域为
，
的定义域为
，则
( )
A.
B.
C.
D.
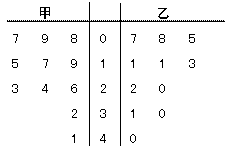2.某赛季，甲、乙两名篮球运动员都参加了11场比赛，
他们每场比赛得分的情况用如图所示的茎叶图表示，
则甲、乙两名运动员的中位数分别是 （ ）
A．
、
B．、
C．
、
D．、
3. 将[0，1）内的均匀随机数转化为[-2，6）的均匀随机数，需实施的变换为 （ ）
A．
B. 
C. 
D.
4. 取一根长度为5 m的绳子，拉直后在任意位置剪断,那么剪得两段的长度都不小于1m的
概率是（ ）
A .
B
. 
C
. 
D. 不能确定
5.已知点
到直线
的距离等于1，则m等于
（ ）
A .
B. 
C.
D. 或
6. 一个射手进行一次射击，有下面四个事件,则正确的是 ( )
事件A：命中环数大于8； 事件B：命中环数大于5；
事件C：命中环数大于4； 事件D：命中环数不大于6；
A. A与D是互斥事件 B. C与D是对立事件
C. B与D是互斥事件 D. 以上都错
7. 一袋中装有大小相同，编号分别为
的八个球，从中有放回地每次取
一个球，共取2次，则取得两个球的编号和不小于15的概率为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
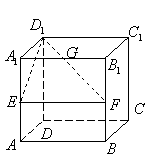
8.在棱长为1的正方体
中，
分别为棱
的中点，
为棱
上的一点，且
．则点到
平面
的距离为 （ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
9. 用秦九韶算法计算多项式
当
时
的值时,需要做乘法和加法的次数分别是 ( )
10.下列与函数
的值域的交集为空集的集合是 ( )
二．填空题(每小题4分,共20分)
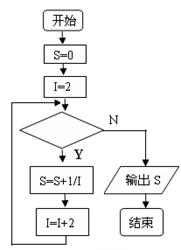
11.下图给出的是计算
的值的一个程序框图，
其中判断框内应填入的条件是 .
12．十进制数335转化为5进制数是____________.
13. 若数据
的平均数
=5，方差
，则
数据
的平均数是
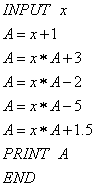，方差为
|
值为2时,输出的结果是
____________________.
|
第二卷
二.填空题答案: (每题5分,共20分)
11. 12.
13. 14.
三、解答题：本大题共6小题，共80分
解答应写出文字说明，证明过程或演算步骤
15．（本小题满分12分）
将一颗质地均匀的正方体骰子（六个面的点数分别为
）先后抛掷两次，
记第一次出现的点数为
，第二次出现的点数为
．
(1) 出现的点数之和为5的概率
（2）求事件“
”的概率；
16. （本小题满分13分）
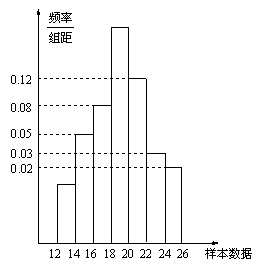
如图是总体的一个样本频率分布直方图，且在[14,16）
内频数为10，在[1２,14）内的小矩形面积为0.02，求：
(1) 求样本容量；
(2) 求在[1２,20）内的频数；
(3) 分别估计样本的众数、中位数.
(保留3位有效数字)
17.(本题13分) 已知图表为人体脂肪含量与年龄的一组抽样数据:
| 人体脂肪含量与年龄 | ||||||
| 年龄 | 37 | 44 | 49 | 53 | 56 | 61 |
| 脂肪含量 | 20.2 | 22.5 | 26.3 | 28.6 | 30.8 | 33.6 |
由资料知脂肪含量y对年龄x呈线性相关关系,参考数据：
，
试求： （1）求
；
（2）线性回归方程
；
（3）估计当一个人年龄为60岁时的脂肪含量. （保留2位小数）
18. (本小题满分14分)
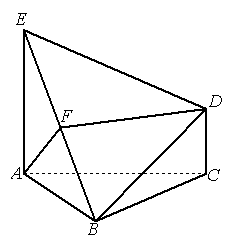
如图，已知
是正三角形，
都垂直于
平面
，且
,
,
是
的中点，
求证：
(1) 
平面;
(2) 
平面
;
(3) 求多面体
的体积
19.(本题14分)
已知圆C：
内有一点
，过点
作直线
交圆
于
两点.
(1)当弦
被点平分时，写出直线的方程；
(2)是否存在直线把圆周分为
的两段弧, 若存在,求出直线的方程,若不存在,
请说明理由.
20. (本题14分)
设二次函数
满足下列两个条件：
①当
时，
的最小值为0，且
成立；
②当
时，
≤
恒成立.
（1）求
的值；
（2）求的解析式；
（3）求最大的实数
(
),使得存在实数
,当
时，就有
恒成立.