高一数学下第二次调查测试

高一数学下第二次调查测试

数学试卷 　   命题人　　罗会元　　 审定　 薛林生

一、　　　　　　 填空题。（每题5分，满分70分）

1、在三棱锥中，直线与的位置关系为_____▲_______.

2、已知正方体的棱长为，则在其六个面上的射影长的和=__▲_.

3、已知则的最大值为_______▲______.

4、已知直线，则直线与所成角的大小为______▲____.

5、设数列为正项等比数列，且，则其公比=　 ▲　

6、用半径为的半圆形铁皮卷成一个圆锥筒，则这个圆锥的高等于__▲___.

7、若一个面体中共有个面是直角三角形，则称这个面体的“直度”为 .由此可知，四棱锥“直度”的最大值为_________▲_______.

8、已知长方体的侧面积为，高为，则长方体对角线长的最小值为 _▲

9、有一根长为，底面半径为的圆柱形铁管，用一段铁丝在铁管上缠绕圈，并使铁丝的两个端点落在圆柱的同一母线的两端，则这段铁丝的最短长度为_____▲___.

10、用棱长为的四个相同正方体木块拼接成一个大的长方体，则长方体的外接球体积的最大值为_____________.

11、已知正三棱锥的侧棱长为，底面边长为，平行四边形的四个顶点分别在棱上，则的最小值为____▲_______.

12、设是两条不同的直线，是三个互不相同的平面，给出下列命题：①若；②；

③；④，

其中正确的命题的序号为____▲_______

13、设等差数列的前项和为，且，则的值为___▲____.

14、已知三棱台中，三棱锥、的体积分别为2、18，则此三棱台的体积的值等于_____▲_______.

请将填空题答案填入下页

江苏省淮阴中学学年度高一下第二次调查测试

数学试卷 　   命题人　　罗会元　　 审校　薛林生

填空题答案

1．　　　　　　  　　　2．　　　　　　  　　　3．　　　　　　 

4．　　　　　　  　　　5．　　　　　　  　　　6．　　　　　　 

7．　　　　　　  　　　8．　　　　　　  　　　9．　　　　　 

10．　　　　　　  　　 11．　　　　　　  　　 12．　　　　　　 

13．　　　　　　  　　 14．　　　　　　  　　　 

二、解答题

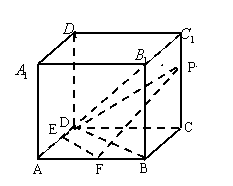15、（14分）已知正方体中，为中点，为中点.在棱上，.

（1）求证：平面；

（2）求四棱锥的体积.

16、（14分）已知函数的最大值为，，.

（1）求的值；（2）解关于的不等式.

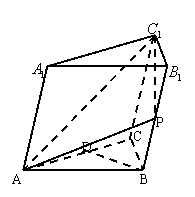
17、（15分）在三棱柱中，平面平面，,为中点，点在棱上，且.

(1)求证：；

（2）当的值等于多少时，就有平面平面？并证明你的结论。

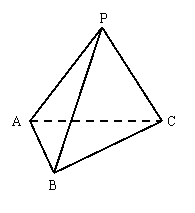18、（15分）在三棱锥中，、、都为直角三角形，试指出的形状，并证明你的结论。

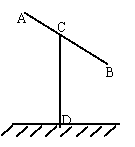
19、（16分）某建筑工地上所用的金属支架由与组成，如图所示，根据要求，至少长，为中点，到的距离比的长小1..已知金属支架的材料每米的价格为10元.

（1）设，试用表示；

（2）怎样设计、的长，可使建造这个支架的成本最低？

20（16分）已知数列满足，，.

（1）　　　 填空：当时，.（填中一个）

（2）　　　 求证：与中一个比大，另一个比小，并指出与中哪一个更接近于.

（3）　　　 若数列的前项和为，求证：.

参考答案及评分标准

一、　　　  填空题

1.　　　异面直线 　　　  2.　　 　　　　　　　3.　　　  1 　　　　　　

4.　　　　　　　　 　　5.　　　　　　　 　6.　　　 　　　　　

7.　　　 　　　　　　 　8.　　　　　　　　 　9.　　 　　 

10.　　　　　　　　 11.　　　　　　　  12.　　  ②③　　　　　 

13.　　　425 　　　　　　 14.　　　 26  　　　　　 

二．解答题

15.解:⑴连AC交EF于G，连PG..................................................................................2’

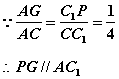...............................................................................................5’

又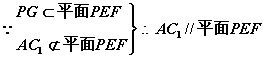..........................................................7’

⑵.........................................................................10’

PC是四棱锥P-EFDB的高　  h=PC=3.....................................................12’

............................................................................................14

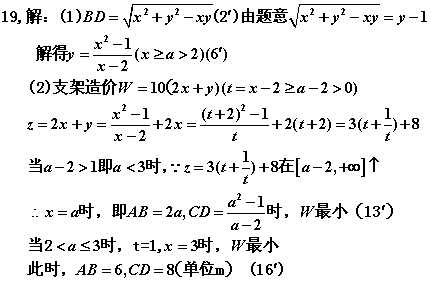
20．解：（1）x_n>1(n≥2)……………………………………………...……..…….2’

　　　 （2）∵a_n+1=b_n+1+4b_n，b_n+1=a_n+b_n

　　　　　  ∴，

　　　　　　  即x_n+1=1+………………………………………….……..6’

　 　　　　　(由x₁==1，知x₂>1,x₃>1,…,x_n>1)

　　　　　  x_n+1=，

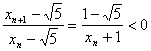
　　　　　  所以x_n+1与x_n中一个比大，一个比小

　　　　　  又∵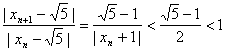

∴x_n+1更接近…………………………………………..……..12’

　　　 （3）由（2）知

　　　　　　 ∴S_n<

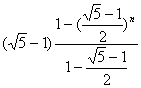　　　　　　　　 =<…………….16’