三角函数与向量的基本概念及综合应用

湖南省省级示范性高中-------洞口三中　方锦昌　提供

一、　　　　　　 向量的基本概念：

1、　向量、平行向量（共线向量）、零向量、单位向量、相等向量：

2、　向量的表示：、、区别于、

3、　向量的加法、减法：平行四边形法则和三角形法则

★　　 例题1、一艘船从A点出发以2km/h的速度向垂直于对岸的方向行驶，同时河水的速为2km/h；求船实际航行的速度大小和方向。（答案：4km/h，方向与水流方向成60°角）

★【※题2】①设O为平面上一定点,A,B,C是平面上不共线的三个点,动点P满足=+l(+),l∈[0,+∞),则点P的轨迹一定通过△ABC的( D　)

A 外心　　　 B 垂心　　　C 内心　　　　D 重心　

②将上题中的条件改为=+l(+)则应选(　C  )

★　　 例题3：（1）、化简下列各式：①+；②+-；③++；④（-）+（-）其中结果为0的有①③④

（ 2）、在平行四边形ABCD中，=,DB=,则有:=-,=+-

4、　实数与向量的积、平面向量基本定理、平面向量的坐标表示：

①　　 注意点的坐标和向量的坐标的差别：②向量的平等行和垂直坐标公式：

　 5、向量的数量积的概念，以及向量平行、垂直、长度、夹角：

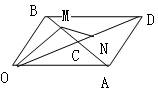
★例1、已知平行四边形OADB中，=,=,AB与OD相交于点C，且BM=BC，CN=CD，用、表示、、和。

　　　 ★ 例2、求证；G为△ABC的重心的充要条件是：++=0

　　　 ★例3、已知AD、BE分别是△ABC的边BC、AC上的中线，=,=，则=____

　　 ★ 例4、①已知等差数列｛a_n｝的前n项之和为S_n,若M,N,,P三点共线，O为坐标原点，且=a₃₁+a₂(直线MP不过点O），则S₃₂等于多少？

　 ②（2006年江西高考）已知等差数列｛a_n｝的前n项之和为S_n,若=a₁+a₂₀₀,且=A,B,C三点共线（该直线不过点O），则S₂₀₀等于（　）

　　　　 A　100　　 B　101　　C 200　　　D　201

　　　 ★例5、①若的起点和终点坐标分别为（1，3），（4，7），则=_____

②　　 已知=(1,2),=(x,1),且+2与2-平行，则x之值为____

③　　 已知=(3,4),⊥,且的起点坐标为(1,2)，终点坐标为 (x,3x)，则等于_____

④　　 已知点M（3，-2），N（-5，-1），且=，则点P的坐标是____（答案：（-1，）

　巩固练习：（一）平面向量的坐标运算规律：①设=(x₁,y₁),=(x₂,y₂),则+=_________；-=__________,l=______；②==；又·=··cos<,>=x₁x₂+y₁y₂则cos<,>==;　　 ③若∥⇔x₁y₂-x₂y₁=0;　　 若⊥⇔x₁x₂+y₁y₂=0，

★例1、 ① 已知=(3,5) =(2,3),=(1,-2),求（·)·　 （答案：（21，-42））

 ②已知=(3,-1),=(-1,2),则-3-2的坐标为_____(答案:(-7,-1))

③已知=4,=3,(2-3)·(2+)=61,求与的夹角.(为120°)

④已知=2,=9, ·=-54,求与的夹角.(为135°)

★　　 例2、①已知=(1,2),=(x,1)且+2与2-平行，则x=_____(答案:)

　　　②已知=2,=1, 与的夹角为,求向量2+3与3-的夹角的余弦值.(答案:)；③已知向量=(cosa,sina),=(cosb,sinb),且≠±,则+与-的夹角大小是____(90°)

④已知向量与的夹角为120°,且=3,+=,则=_____

★例3已知=(1,2),=(-3,2),当k为何值时,①k+与-3垂直?②k+与-3平行,平行时它们是同向还是反向?（解:①k=19; ②k=-1/3,反向.）

★例4:①若向量+3垂直于向量7-5,且向量-4垂直于向量7-2,求向量与的夹角大小.(答案:60°)

②已知向量=(2,7),=(x,-3),当与的夹角为钝角时，求出x的取值范围；若与的夹角为锐角时，问x的取值范围又为多少？（答案：为钝角时x<,x≠; 为锐角时x>)

★例5、已知=(cos,sin),=(sin,cos),x∈[0,]，①求·；②求+，③设函数¦（x)=·++，求出¦(x）的最大值和最小值。

解：·=sin2x; +=(sinx+cosx), ¦(x）的最大值为1+2，最小值2

★　　 例6、已知向量a=(sinq,1),b=(1,cosq),-<q<,①若a⊥b,求出q之值，②求出a+b的最大值。（答案：q=-，a+b的最大值+1）

★例7、①已知向量=(cosq,sinq),向量=(,-1)，求2-的最大值。（答案为4）

②已知向量=(3,1),向量=(x,-3),且⊥，求出x之值。（答案为1）

③已知=3,=2,且与的夹角为60°，当m为何值时，两向量3+5与m-3互相垂直？（答案：m=）

④已知=3,=8,向量与的夹角为120°，则+之值为多少？（答案：7）

⑤已知==1,及3-2=3，求出3+之值。（答案：2）

⑥已知,是非0向量，且满足-2⊥,和-2⊥，则与的夹角为多少？（答案：为60）；⑦已知向量=(4,-3),=1,且·=5,则=_______（答案：（，）

⑧若向量与的夹角为60°，且=4，又有(+2)·(-3)=-72，则向量的模为多少？（答案：为6）；⑨已知点A（-2，0），点B（3，0），动点P（x,y)满足·=x²,则动点P的轨迹方程为____（答案：y²=x+6)

⑩在△ABC中，a,b,c分别为角A，B，C的对边，且a+c=2b,A-C=，求sinB（答案：）

★例8、已知向量,,且=4,=3,又(2-3)·(2+)=61,则<,>=_____（120°）

★例9、已知两点M（-1，0），N（1，0），且点P使·，·，·成公差小于0的等差数列，①求点P的轨迹方程；②若点P的纵坐标为，求tan<,>之值。（答案：①x²+y²=3(x>0);②)

★　　 例10、已知=(1,-2),=(1,l),①若和的夹角为锐角，求l的取值范围；②若和垂直，求l之值；③若和的夹角为钝角，求l的取值范围；④若和同向，求l的值；⑤若和反向，求l的值；⑥若和共线，求l的值。

★　　 例11、已知=(-3,2),=(2,1),=(3,-1),t∈R,①若-t与共线，求实数t之值。②求出+t的最小值及相应的t之值。

四、三角与与向量的综合归纳

1、三角变形公式主要是：

①诱导公式；②sin(a±b),cos(a±b),tan(a±b);③sin2a,cos2a,tan2a;③sin²a,cos²a;④asinq+bcosq;

⑤注意常数代换（如1= sin²a+cos²a;=sin30°=cos60°等；角的配凑（如a=（a+b）-b，2a=（a+b）+（a-b），a=+等）

2、变形时，要注意角与角之间的相互关系，最常用的有：切割化弦、高次降幂、异角化同角等；（化同名、化同次、化同角）

3、三角函数的图象和性质，要注意定义域、值域、奇偶性、图象对称性、周期性、单调性、最值；正、余弦函数作图的“五点法”，以及图象的变换。

4、解三角形时，要充分利用正弦定理、余弦定理，结合三角形的内角和定理，三角变形公式去处理问题；

5、向量要注意选择几何、字符、坐标运算形式，力求简化运算过程；要将坐标运算与基底运算灵活

加以应用；向量的数量积是解决有关平行、垂直、夹角、模、投影等问题的重要工具；利用²=·

=²可以实现数量积与模的相互转化。

　　　 【※题1】①已知=(1,1)与+2的方向相同,则·的取值范围是_______(答案:(-1,+∞))

②已知非零向量与满足(+)·=0,且·=,则△ABC为(D　)

A钝角△　　　B Rt△　　C 等腰非等边△　　D　等边△

③已知=(3,1),=(-1,2),若⊥,且∥,则=________(答案:(14,7))

④已知向量=(1,-2),=(1,l),若与的夹角为锐角,则实数l的取值范围是_____(答案:(-∞,-2)∪(-2,))

　　　 【※题2】设函数¦(x)= ·,其中向量=(2cosx,1),=(cosx,sin2x),①当¦(x)=1-,且x∈[-,],求x； ②若函数y=2sin2x的图象按向量=(m,n)(m<)平移后得到函数y=¦(x)的图象，求实数m,n之值。

解:①¦(x)=2sin(2x+)+1,则x=-；②m= , n=1

★【※题3】①已知tan(a-π)=,则(2sina+cosa)cosa的值为（  A　）

A 　　B 　　 C 1　　 D 0

②已知a、b∈（，π），sin(a+b)=,sin(b-)=,则cos(a+)=__________(答案：）

③已知¦（x)=2tanx-,则是¦（）的值为（　）

A 4　　　　 B 　 C 4　　　  D　8　（解、¦（x)=,则所求为8）

★【※题4】①设△ABC的三个内角A，B，C的对边分别为a,b,c,若a,b,c成等比数列，且c=2a,则cosB=( B )

A 　　　B　　　　 C 　　　　D

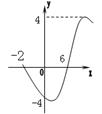
②已知某正弦函数y=Asin(ωx+j)的部分图象如图示，则¦（x)的解析式为________(答案:y= y=-4sin(x+)

③函数y=sin(2x-)的图象是由函数y=cos2x的图象经过下列哪种平移变换而得到的(　D ) A 向左平移个单位　 B向右平移个单位　 C向左平移个单位　D向右平移个单位

★【※题5】①设点P是函数¦(x)=sinωx的图象C的一个对称中心,若点P到图象C的对称轴的距离的最小值是,则¦(x)的最小正周期是_______(答案:π)

②已知函数¦(x)=sin (r>0)的图象上的一个最大值点和一个最小值点都在圆x²+y²=r²上,则¦(x)的最小正周期是______(答案:4)

③已知函数y=sin(ωx+j)(ω>0,0<j<π)是偶函数,其图象关于点M(,0)对称,且在[0,]上是单调函数,求ω和j的值.(答案:j=;ω=2或)

★【※题6】已知函数¦(x)= sinωxcosωx-cos²ωx+(ω≠0)的最小正周期是π,且图象关于直线x= 对称,①求出ω之值; ②若当x∈[0,]时,a+¦(x)<4恒成立,求实数a的取值范围.

解、①¦(x)= -sin（2x+）+1；②a+¦(x)<4恒成立Þ[-4-¦(x)]_max<a<[4-¦(x)]_min

则a∈（-4，）

★【※题7】①把函数y=cosx-sinx的图象向左平移m个单位之后，所得图象关于y轴对称，则m的最小值是（ C ）A 　 B 　 C 　　 D

②若¦(x)= asin(x+)+3sin(x-)是偶函数，则a=______(答案:-3)

③把曲线C:y=sin(-x)cos(x+)向右平移a(a>0)个单位,得到曲线C′,若曲线C′关于点(,0)对称,则a的最小值是_____(答案:)

★【※题8】受日月引力,海水会发生涨落,这种现象叫做潮汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋.某港口水的深度y(米)是时间t(0≤t≤24,单位:时)的函数,记作y=¦(t),下面是该港口在某季节每天水深的数据:

t(时)	0	3	6	9	12	15	18	21	24
y(米)	10.0	13.0	9.9	7.0	10.0	13.0	10.1	7.0	10.0

经过长期观察, y=¦(t)曲线可以近似地看作函数y=Asinωt+k的图象

①根据以上数据,求出函数y=¦(t)的近似表达式; ②一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时,认为是安全的(船舶停靠时,船底只要不碰海底即可).某船吃水深度(船底离水面的距离)为6.5m,如果该船想在同一天内安全进出港口,问它至多能在港内停留多长的时间(忽略进出港口所需时间)

解:①y=3sint+10;　 ②y=3sint+10≥5+6.5,则1≤t≤5或13≤t≤17,则最多可停留16个小时.

　　　 【※题9】设△ABC的三个内角A,B,C的对边分别是a,b,c,

(Ⅰ)给出下列两个条件:➊a,b,c成等差数列; ➋a,b,c成等比数列;

(Ⅱ)给出下列三个结论:①0<B≤;②a·cos²()+c·cos²()=;③1<≤

请你选择给定的两个条件中的一个做为条件,给定的三个结论中的两个做为结论,组建一个你认为正确的命题,并给出证明.

解:（1）可组建四个正确的命题:➊Þ①②;➊Þ①③；➊Þ②③；➋Þ①③

（2）y= = sin(B+）且0<B≤，则1<y≤

一、综合巩固练习（1）

★　　 例1：化简： ①··　　(答案：sinq)

②化简：sin(a-)+cos(a+)　　 (答案：0）

③已知π<a<2π，cos(a-9π)=,求cot(a-)的值　 （答案：原式=-tana=4/3)

★1、函数y= + + +的值域为（B）：

A｛-2，4　｝B ｛-2，0，4｝ C ｛-2，0，2，4｝D ｛-4，-2，0，4｝

★2、设函数¦（x)=asin(πx+a)+bcos(πx+b),其中a,b,a,b均为非0实数，且有¦（2003）=1，求¦（2004）之值　 （答案：-1）

★3、已知sina是方程5x²-7x-6=0的一个根，求之值

解；sina=,则所求为-tan²a=

★4、①求sincosπtan(-)之值　 （答案：）

※②已知tan(5π+a)=m,则之值为多少？（答案）

★5、（2006·湖南省·文科·16题·12分）已知sinq - ·cosq=1,q∈(0,π),求q之值

解：化简得sinq -2sin²q=0,则sinq=0（舍去）或，则q=或

★　　 6、（2006·天津·文科·17题·12分）已知tana+cota=5/2,a∈(,)求cos2a和sin(2a+)之值。（答案：∵tana=2, cos2a=和sin(2a+)=)

★　　 7、（2006·安徽·文科·17题·12分）已知a为锐角，且sina=,求①之值；②求tan(a-)的值。（答案 ：①20；②）

★　　 8、已知sin(kπ+q)=-2cos(kπ+q)(k∈Z),求下列各式：①5cos²q+3sinqcosq;②;③tanq(cosq-sinq)+

解：①； ②10；　③sinq=±

二、　　　　　　 巩固练习（2）：

三角变形的主要的公式有：①a±b的正弦、余弦、正切；②sin2a，cos2a,tan2a,③sin²a,cos²a,④asinq+bcosq

★例1、辅助角公式的应用：①sinx±cosx　　②sinx±cosx　③ sinx± cosx　 ④sinx±cosx　　 ⑤3sinq±3cosq

★例2 化简：1-sin²2a-sin²(a-)-cos⁴a (为(sin2a-cos2a)

★例3 ①cos113°cos23°+sin113°cos67°

　　　　②　　 ③　

（答案：①cos90°=0,②tan30=,③2-)

★题4、（2006·广东·15题·14分）已知函数¦（x)=sinx+sin(x+),x∈R,

①　　 求¦（x)的最小正周期； ②求¦（x)的最大值和最小值； ③若¦（a)=3/4，求sin2a之值。（答案：①2π，②±；③

★题5、（2006·陕西·17题·12分）已知已知函数¦（x)=sin（2x-）+2sin²(x-),（x∈R）,① 求¦（x)的最小正周期； ②求使¦（x)取得最大值的x的集合；

答案：①π；②所求x的集合为：｛xkπ+,k∈Z｝

★题6、（2006·湖北·16题·12分）设向量=(sinx,cosx),=(cosx,cosx),x∈R,函数¦（x)=·(+),① 求函数¦（x)的的最大值和最小正周期； ②求使不等式¦（x)≥成立的x的取值范围的集合

答案 ；最大值为+，最小正周期为π，所求x的集合为：｛xkπ-≤x≤kπ+,k∈Z｝

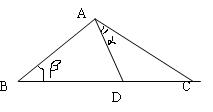★题7、（2006·湖南·16题·12分）如图，D是直角三角形△ABC斜边BC上的一点，且AB=AD，记∠CAD=a，∠ABC=b，

①　　 证明sina+cos2b=0; ②若AC=DC，求b的值。

(答案：b=)

★题8、（2006·江西·19题·12分）在锐角三角形△ABC中，角A，B，C的对边分别为a,b,c,已知sinA=2/3，①求tan²()+sin²()的值；②若a=2,S_△ABC=，求b的值。(答案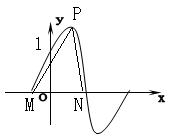：①，②b=)

★题9、（2006·浙江·16题·14分）如图，函数y=2sin(πx+j),(x∈R)（其中0≤j≤）的图象与y轴交于点（0，1）；①求j的值；②设P为图象上的最高点，M，N是图象与x轴的交点，求与的夹角。（答案：j=；夹角为arccos)

（三）巩固练习（3）：

★【※题1】函数¦(x)=tanωx(ω>0)的图象的相邻两支截直线y=所

得的线段长为,则¦（）之值是( A )　A 0　　B 1　　　C -1　　D　

★【※题2】已知=(cosa,sina),=(cosb,sinb),且与之间满足关系:k+=-k,其中k>0,则·的最小值是___,此时与的夹角大小为_______

解、平方得·=≥则最小值为,此时与的夹角大小为60°

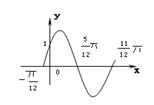★【※题3】函数¦₁(x)=Asin(ωx+j)(A>0,ω>0,j<)的一段图象过点(0,1),如图所示,①求函数¦₁(x)的解析式；②将函数y=¦₁(x)的图象按向量=(,0)平移,得到函数y=¦₂(x)的图象,求函数y=¦₁(x)+ ¦₂(x)的最大值,及此时自变量x的取值集合.　　　解、①¦₁(x)=2sin(2x+)；　 ②y=¦₂(x)= -2cos(2x+)　y=¦₁(x)+ ¦₂(x)= 2sin(2x-) 当x=kπ+π(k∈Z)时,y_max=2

★【※题4】◆①若函数¦(x)=sin3x-cos3x在区间M上的最大值与最小值的差等于4，则区间M 一定不可能是（ C　）

A [-，]　　B [-π，-]　　C [，]　　D [，π]

◆②设函数¦(q)=acos²q+bsin²q+2acosq,其中a≠b≠0,q∈[0,π]则关于q的方程¦(q)=0的解有(　)个　A 0　　 B　1　　　C 2　　　　　  D 无数个

解、¦(q)=(a-b)cos²q+2acosq+b=(a-b)t²+2at+b　(-1≤t≤1)则¦(-1)·¦(1)=-3a²<0又△>0从而选(B)；★【※题5】在三角形ABC中,若·+·+·=-6

①若∠C为直角,求c边的长；②若三角形的周长等于6,试判断三角形ABC的形状

解、①利用余弦定理，则有c=;②可判断出△ABC为正三角形

★【※题6】函数¦(x)=Asin(ωx-)(A>0,ω>0)的图象经过点(π,2)，且其单调递增区间的最大长度是2π，求出其单调递减区间。（解、A=4，周期为4π，则有ω=，从而¦(x)=4sin(x-)，则单调递减区间为[+4kπ, +4kπ] (k∈z)

★【※题7】已知向量=(sinx,cosx),=(cosx,cosx),=(2,1),①若∥,求sin2x的值;②设函数¦(x)=·,△ABC的三边a,b,c满足b²=ac,且¦(B)=1,试判断△ABC的形状

解、①∥则tanx=2，则sin2x=　　　  ②¦(x)= +sin(2x+),由¦(B)=1则B=。又由余弦定理有a=c,从而为正三角形

★【※题8】已知=(,),=-,=+,若△AOB是以O为直角顶点的等腰直角三角形,则向量=_____,△AOB面积为_____

解、⊥且=,则旋转90°画图知=(,)或（，），△AOB面积是1

★【※题9】若把函数的图象沿向量a=（-，-2）平移后，得函数y=cosx的图象，则原函数的解析式为（ A ）A y=cos(x-)+2　B y=cos(x+)+2　 C y=cos(x-)-2　　D y=cos(x+)-2

★【※题10】设向量=(cosx,sinx),=(sinx,-sinx),①求函数¦（x)=log_a(·+) (a>0且a ≠1)的单调递增区间； ②若·=，且x∈(0,),求满足sin(x-q)-sin(x+q)+sin2x=的最小正角q。（解、¦（x)= log_a(sin2x+)则①当a>1时，↗为（kπ-,kπ+);

②0<a<1时，↗为（kπ+,kπ+)　 ③最小正角q=

四、巩固练习(4)

★【※题1】已知A(3,0),B(0,3),C(cosa,sina), ①若· =-1,求sin2a之值　

 ②若+=,且a∈(0,π),求与的夹角

解、sin2a=-5/9　 与的夹角为30°

★【※题2】已知¦（x)=asin(πx+a)+bsin(πx-b),其中a、b、a、b均为非零实数，若¦（2005）= -1，则¦（2006）之值为（ B  ）：A 0　 B　1　 C -1　 D　 2003

 ★【※题3】已知向量=(4cosB,cos2B-2cosB),=(sin²(+),1),且¦（B)=·

 ①若¦(B)=2,且0<B<π,求角B; ②若对任意的角B∈(0,), ¦(B)-m>2恒成立,求实数m的取值范围.（解、①¦(B)= ·=2sin(2B+),B=;②m<2sin(2B+)-2恒成立,则m∈（-∞，--2]

★【※题4】已知¦（x)=sin(x+)+sin(x-)+cosx+a(a∈R,a为常数,x∈R);　

①求函数¦（x)的最小正周期;　　②若函数¦（x)的最大值为3,求实数a之值;

③求函数¦（x)的递减区间.

解、①¦（x)=2sin(x+)+a，则最小正周期T=2π；　② a=1;　 ③函数¦（x)的递减区间为[2kπ+,2kπ+] (k∈z)

★【※题5】已知函数¦（x)= ,①若函数¦（x)的定义域为（0，），求函数¦（x)的单调递减区间；②若¦（x)=-2，求x之值。

解、①¦（x)=2sin(x+)，¦（x)的单调递减区间为[，）；②x=kπ-,(注意：x=kπ-时，cos2x=0,应舍去）

五、巩固练习（5）：

1、y=sinx,y=cosx,y=tanx的图象和性质； 以及五点做图法的应用。

2、　y=Asin(ωx+j),y=Acos(ωx+j)的周期、奇偶性、对称轴、单调性、最值。

3、　巩固练习：①如果函数y=sin2x+acos2x的图象关于直线x=-对称，则a=( D　)

A 　　 B -　　C 1　　D　-1

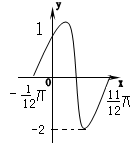②求下列函数的周期：➊y=sinx+cosx;　➋y=sin(2x+)cos2x;　➌y=cos²4x; ➍y=tanx-cotx;

③求函数y=cos²x-3cosx+2的最小值（答案为0）

★例1已知函数y=2sin(ωx+j)(j<)的图象，①求出ω、j的值；

②求出函数图象的对称轴方程，对称中心的坐标，最小正周期。

　解：①ω=2，j=；②对称轴方程为：x= +;对称中心的坐标为（ - ,0)，最小正周期为π；★例2、函数y=3sin(2x+)的图象可以看成是把函数y=3sin2x的图象经过怎样的平移变化而得到的？

★例2、设函数y=sin²x+sinxcosx+a，①求¦（x)的递增区间； ②当x∈[0,]时，¦（x)的最小值为2，求出a的值，并说明此时经过怎样的变换，¦（x)的图象可变为y=sinx的图象。（答案：a=2）

★例3、求函数¦(x)=的最小正周期、最大值、单调递增区间

★例4、已知在△ABC中，sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小。

解、A=， B =，C=

★例5、(2006年福建·17题·12分）已知函数¦(x)= sin²x+sinxcosx+2cos²x,x∈R，① 求函数¦（x)的最小正周期和单调增区间；②函数¦（x)的图象可以由函数y=sin2x(x∈R）的图象经过怎样的变换而得到？

★例6、(2006年山东·17题·12分）已知函数¦(x)==Asin²(ωx+j)（A>0，ω>0，0<j<），且y=¦(x)的最大值为2，其图象相邻两对称轴间的距离为2，并过点（1，2）；①求j；②计算¦（1）+¦（2）+…+¦（2008）

解、j=，¦（1）+¦（2）+…+¦（2008）=4×502=2008

★例7、已知A，B，C是△ABC的在个内角，向量=(-1,),=(cosA,sinA),且·=1;①求角A；②若,求tanC

解、A=，tanC= (注意：当tanB=-1时，cos²B-sin²B=2)

六、巩固练习（6）：　

 ★例1、平面内有两点A（1，cosx),B(cosx,1),其中x∈[-,],①求向量OA与OB的夹角q的余弦值；②记¦（x)=cosq，求¦(x)的最小值。

解：① cosq = ；② ¦(x) = ，而2≤cosx+≤，则¦(x)的最小值为，（注意：最大值才是1）

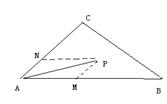
★　　 例2、 如图，点P是△ABC内一点，且=+，则△ABP的面积与△ABC的面积之比是_____

解：由向量的平行四边形法则，则=，从而所求之比为

★　　 3、函数¦（x)=cos(π-x)·lgx在区间[，]内的图象是

　　　　　　　　　 

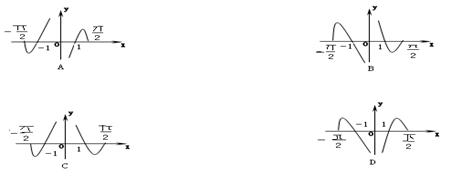
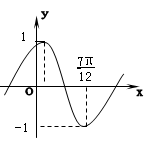★4、将函数y=sinωx(ω>0)的图象按向量=(,0)平移，平移后　　的图象如图所示，则该图象所对应的函数的解析式是（　 ）

A　y=sin(x+)　　　　 B　　y=sin(x-)

C　y=sin(2x+)　　　　D　 y=sin(2x-)

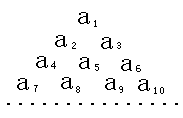★5、在直角坐标系中，横坐标和纵坐标均为整数的点叫做格点，若函数y=¦(x)的图象恰好经过k个格点，则称函数y=¦(x)为k阶格点函数 。给出下列四个函数:① y=sinx;② y=log₂x;③ y=e^x-1;④ y=x²;其中为一阶格点函数的函数个数共有（　）个　　

 A　1　　　 B 2　　　C 3　　　　  D　4

★　　 6、已知数列｛a_n｝是首项为1，公差为2的等差数列，将数列｛a_n｝中的各项排成如图所示的一个三角形数表，记A（i,j)表示第i行从左至右的第j个数，例如A（4，3）=a₉,则A（10，2）=（　 ）

A 91　　　  B　93　　　 C　95 　　 D　97

★7、定义运算a◆b为： a◆b=　a (a≤b)

　　　　　　　　　　　　　　  　b (a>b)　 则1◆2^x的取值范围是______

★8、如果对某对象连续施加两次相同的变换，其结果还是变换前的对象，则称这种变换叫做“回归变换”，例如，对于一个实数a,其相反数的相反数仍是a，所以“取实数的相反数”是一种回归变换。那么，对于任意的实数x,线性变换y=kx+b(k、b∈R，b≠0)是回归变换的充要条件是_____

★9、某公司拟投资13亿元进行项目开发，现有6个项目可供选择，其投资额和利润如下表所示：

项目	A	B	C	D	E	F
投资额（亿元）	5	2	6	4	6	1
利润（千万元）	０．５５	０．４	０．６	０．５	０．９	０．１

设计一个投资方案,使投资13亿元所获得的利润最大,则应选的项目是______(只需写出投资方案中的项目的代号)

★10、设a为实常数，函数¦(x)= +sinx,若存在x₀∈(,π)，使得a¦(x₀)=1+a成立，求出a的取值范围。

★11、某工厂有容量为300吨的水塔一个，每天从早上6点起到晚上10点止供应该厂生活和生产用水，已知该厂生活用水是10吨/小时，工业用水W吨与时间t (单位：小时，且定义早上6点时t=0) 的函数关系式为W=100，水塔进水量有10级，第一级每小时进水10吨，以后每提高一级，每小时进水就增加10吨，若某天水塔原有水量是100吨，且在供水的同时又打开进水管，请你设计进水量的级数，使得水塔既能保证该厂用水 (水塔中的水不空)，又不会使水溢出。