平面与平面平行的判定与性质
一、选择题
1．平面α∥平面β，点A、C∈α，点B、D∈β，则直线AC∥直线BD的充要条件是（ ）
A．AB∥CD B．AD∥CB
C．AB与CD相交 D．A、B、C、D四点共面
2．“α内存在着不共线的三点到平面β的距离均相等”是“α∥β”的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要的条件
3．平面α∥平面β，直线aÌα，P∈β，则过点P的直线中（ ）
A．不存在与α平行的直线 B．不一定存在与α平行的直线
C．有且只有—条直线与a平行 D．有无数条与a平行的直线
4．下列命题中为真命题的是（ ）
A．平行于同一条直线的两个平面平行
B．垂直于同一条直线的两个平面平行
C．若—个平面内至少有三个不共线的点到另—个平面的距离相等，则这两个平面平行．
D．若三直线a、b、c两两平行，则在过直线a的平面中，有且只有—个平面与b，c均平行．
5．已知平面α∥平面β,且α、β间的距离为d，lÌα，l′Ìβ,则l与l′之间的距离的取值范围为（ ）
A．（d，∞） B．（d，＋∞） C．{d} D．（0，∞）
6．已知直线a、b、cÌα，且a∥β、b∥β、c∥β，则“a、b、c到平面β的距离均相等”是“α∥β”的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要的条件
7．给出以下命题：
①夹在两个平行平面间的线段，较长的与平面所成的角较小；
②夹在两个平行平面间的线段，如果它们的长度相等，则它们必平行；
③夹在两个平行平面间的线段，如果它的长度相等，则它们与平面所成的角也相等；
④在过定点P的直线中，被两平行平面所截得的线段长为d的直线有且只有一条，则两平行平面间的距离也为d
其中假命题共有（ ）
A．1个 B．2个 C．3个 D．4个
8．设α∥β，P∈α，Q∈β当P、Q分别在平面α、β内运动时，线段PQ的中点X也随着运动，则所有的动点X（ ）
A．不共面
B．当且仅当P、Q分别在两条平行直线上移动时才共面
C．当且仅当P、Q分别在两条互相垂直的异面直线上移动时才共面
D．无论P、Q如何运动都共面
二、填空题
9．已知α∥β且α与β间的距离为d，直线a与α相交于点A与β相交于B，若
，则直线a与α所成的角＝___________．
10．过两平行平面α、β外的点P两条直线AB与CD，它们分别交α于A、C两点，交β于B、D两点，若PA＝6，AC＝9，PB＝8，则ＢD的长为__________．
11．已知点A、B到平面α的距离分别为d与3d，则A、B的中点到平面α的距离为________．
12．已知平面α内存在着n个点，它们任何三点不共线，若“这n个点到平面β的距离均相等”是“α∥β”的充要条件，则n的最小值为_________．
三、解答题
13．已知平面α∥平面β直线a∥α，aËβ，求证：a∥β．
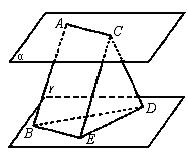
14．如图，平面α∥平面β，A、C∈α，B、D∈β，点E、F分别在线段AＢ、CD上，且
，求证：EF∥平面β．
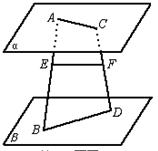
15．P是△AＢC所在平面外一点，A′，B′，C′分别是△PＢC、△PCA、△PAＢ的重心，
（1）求证：平面A′Ｂ′C′∥平面AＢC；
（2）求S△A′Ｂ′C′∶S△AＢC．
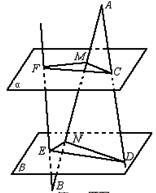
16．如图已知平面α∥平面β，线段AＢ分别交α、β于M、N，线段AD分别交α、β于C、D，线段ＢF分别交α，β于F、E，若AM＝m，ＢN＝n，MN＝P，求△END与△FMC的面积之比．
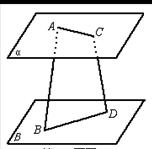
17．如图，已知：平面α∥平面β，A、C∈α，B、D∈β，AC与ＢD为异面直线，AC＝6，ＢD＝8，AＢ＝CD＝10，AＢ与CD成60°的角，求AC与ＢD所成的角．
参考答案
一、选择题
1．D 2．B 3．C 4．B 5．B 6．C 7．A 8．D
二、填空题
9．60° 10．12 11．d或2d 12．5
三、解答题
13．证明：取平面α内一定点A，则直线a与点A确定平面g，设g∩α＝b，g∩β＝c，
则由a∥α得a∥b，由α∥β得b∥c，于是a∥c．
又∵aËβ，∴a∥β．
14．证明：（1）若直线AB和CD共面，
∵α∥β，平面ABDC与α、β分别交于AC、BC两直线，
∴AC∥BD．又∵
＝
，
∴EF∥AC∥BD，∴EF∥平面β．
（2）若AB与CD异面，连接BC并在BC上取一点G，使得＝
，则在△BAC中，EG∥AC，ACÌ平面α，
∴EG∥α．又∵α∥β，
∴EG∥β；同理可得：GF∥BD，而BDÌβ，
又∵GF∥β．∵EG∩GF＝G，∴平面EGF∥β，
又∵EFÌ平面EGF，∴EF∥β．
综合（1）（2）得EF∥β．
15．证明：（1）连接PA′、PB′、PC′，分别交BC、CA、AB于K、G、H，连接GH、KG、HK．
∵B′、C′均为相应三角形的重心，
∴G、H分别为AC、AB的中点，且
＝
＝
，
∴B′C′∥GH，同理A′B′∥KG，A′B′∩B′C′＝B′且GH∩KG＝G，
从而平面A′B′C′∥平面ABC．
（2）由（1）知△A′B′C′∽△KGH，
∴
＝
＝
，
又∵S△KGH＝
S△ABC，∴S△A′B′C′＝
S△ABC，
∴S△A′B′C′∶S△ABC＝1∶9．
16．证明：∵α∥β，平面AND分别交α，β于MC、ND，
∴由面面平行的性质定理知，MC∥ND，同理MF∥NE；又由等角定理：“一个角的两边分别平行于另一角的两边且方向相同，则两角相等”知：∠END＝∠FMC，从而
＝
，
＝
，
∴ND＝
·MC＝
·MC，NE＝·MF＝
·MF．
∴S△END＝
ND·NE·sin∠END
＝···MC·MF·sin∠FMC
＝
·S△FMC．
∴
＝．
即：△END与△FMC的面积之比为．
17．由α∥β作BE
AC，连结CE，则ABEC是平行四边形．∠DBE是AC与BD所成的角．∠DCE是AB、CD所成的角，故∠DCE＝60°．
由AB＝CD＝10，知CE＝10，于是△CDE为等边三角形，
∴DE＝10．
又∵BE＝AC＝6，BD＝8，
∴∠DBE＝90°．
∴AC与BD所成的角为90°．
