直线与平面垂直的判定与性质
一、选择题
1．两异面直线在平面α内的射影（ ）
A．相交直线 B．平行直线
C．一条直线—个点 D．以上三种情况均有可能
2．若两直线a与b异面，则过a且与b垂直的平面（ ）
A．有且只有—个 B．可能存在也可能不存在
C．有无数多个 D．—定不存在
3．在空间，下列哪些命题是正确的（ ）
①平行于同一条直线的两条直线互相平行；
②垂直于同一条直线的两条直线互相平行；
③平行于同一个平面的两条直线互相平行；
④垂直于同—个平面的两条直线互相平行．
A．仅②不正确 B．仅①、④正确 C．仅①正确 D．四个命题都正确
4．若平面α的斜线l在α上的射影为l′，直线b∥α，且b⊥l′，则b与l（ ）
A．必相交 B．必为异面直线 C．垂直 D．无法确定
5．下列命题
①平面的每条斜线都垂直于这个平面内的无数条直线；
②若一条直线垂直于平面的斜线，则此直线必垂直于斜线在此平面内的射影；
③若平面的两条斜线段相等，则它们在同一平面内的射影也相等；
④若一条线段在平面外并且不垂直于这个平面，则它的射影长一定小于线段的长．
其中，正确的命题有（ ）
A．1个 B．2个 C．3个 n 4个
6．在下列四个命题中，假命题为（ ）
A．如果一条直线垂直于平面内的无数条直线，那么这条直线和这个平面垂直
B．垂直于三角形两边的直线必垂直于第三边
C．过点A垂直于直线a的所有直线都在过点A垂直于a的平面内
D．如果三条共点直线两两垂直，那么其中一条直线垂直于另两条直线确定的平面
7．已知P是四边形ABCD所在平面外一点且P在平面ABCD内的射影在四边形ABCD内，若P到这四边形各边的距离相等，那么这个四边形是（ ）
A．圆内接四边形 B．矩形 C．圆外切四边形 D．平行四边形
8．在△ABC中，AB＝AC＝5，BC＝6，PA⊥平面ABC，PA＝8，则P到BC的距离等于（ ）
A．
B．
C．3 D．4
二、填空题
9．AB是平面α的斜线段，其长为a，它在平面α内的射影A′B的长为b，则垂线A′A_________．
10．如果直线l、m与平面α、β、γ满足：l＝β∩γ，l⊥α，mÌα和m⊥γ，现给出以下四个结论：
①α∥γ且l⊥m；②α
γ且m∥β③αβ且l⊥m；④αγ且l⊥m；其中正确的为“________”．（写出序号即可）
11．在空间四面体的四个面中，为直角三角形的最多有____________个．
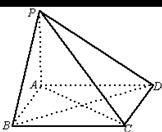
12．如图，正方形ABCD，P是正方形平面外的一点，且PA⊥平面ABCD则在△PAB、△PBC、△PCD、△PAD、△PAC及△PBD中，为直角三角形有_________个．
13．给出以下四个命题
（1）两条平行直线在同一平面内的射影一定是平行直线；
（2）两条相交直线在同一平面内的射影一定是相交直线；
（3）两条异面直线在同一平面内的射影—定是两条相交直线；
（4）一个锐角在平面内的射影一定是锐角．
其中假命题的共有_________个．
14．若一个直角在平面α内的射影是一个角，则该角最大为___________．
三、解答题
15．已知直线a∥平面α,直线b⊥平面α，求证：a⊥b．
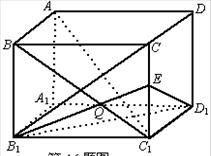
16．如图，在长方体AC1中，已知AB＝BC＝a，BB1＝b（b＞a），连结BC1，过Bl作B1⊥BC1交CC1于E，交BC1于Q，求证：AC⊥平面EBlD1
17．如图在△ABC中，已知∠ABC＝90°，SA⊥△ABC所在平面，又点A在SC和SB上的射影分别是P、Q．
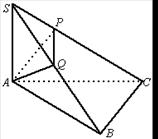
求证：PQ⊥SC．
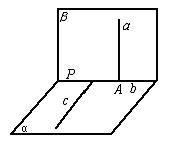
18．已知在如图中，∠BAC在平面α内，点PÏα，PE⊥AB，PF⊥AC，PO⊥α，垂足分别是E、F、O，PE＝PF，
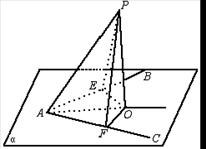
求证：∠BAO＝∠CAO，
19．已知：点P与直线a，试证；过点P与a垂直的直线共面．
20．四面体ABCD的棱AB⊥CD的充要条件是AC2＋BD2＝AD2＋BC2．
四、思考题
对于一个三角形，它的三条高线总相交于—点，而对于一个四面体，它的四条高线是否总相交于一点呢?若不总相交于一点，则怎样的四面体其四条高线才相交于一点呢?这是一个美丽而非凡的问题，请读者进行研究拓展．
参考答案
一、选择题
1．D 2．B 3．B 4．C 5．A 6．A 7．C 8．D
二、填空题
9．
10．③、④ 11．4 12．5 13．4 14．180°
三、解答题
15．证明：设β为过a的平面，且α∩β＝l．
∵a∥α，∴a∥l．
∵b⊥l，∴b⊥a．
16．证明：∵AB⊥面B1C，BC1为AC1在平面B1C上的射影，且B1E⊥BC1，∴由三垂线定理知B1E⊥AC1．
又∵AA1⊥面A1C1，AB＝BC，A1C1⊥B1D1，A1C1是AC1在面A1C1上的射影
∴由三垂线定理得AC1⊥B1D1．
又∵B1E∩B1D1＝B1，
∴AC1⊥平面EB1D1．
17．证明：∵SA⊥面ABC，BCÌ面ABC，
∴SA⊥BC．
又∵AB⊥BC且SA∩AB＝A，
∴BC⊥面SAB，AQÌ面SAB．
∴BC⊥AQ，又AQ⊥SB，BC∩SB＝B．
∵AQ⊥面SBC．
∴PQ是斜线AP在平面SBC上的射影，
又∵AQ⊥SC，
∴由三垂线定理的逆定理可得PQ⊥SC．
18．证明：∵PO⊥α，PE＝PF，
∴OE＝OF，
又∵PE⊥AB、PF⊥AC，
∴OE⊥AB、OF⊥AC．
故Rt△AOE≌Rt△AOF，
∴∠BAO＝∠CAO．
19．证明：如图，在点P和直线a所在的平面β内，过点P作直线a的垂线b，设垂足为A．设过点P与β垂直的直线为c，则必有c⊥a，再设由b、c确定的平面为α，则必有a⊥α．
设l是过点P与a垂直的直线，下证：lÌα．
若lËα，设由l与c确定的平面为α′，
则由a⊥l，a⊥c，l∩c＝P，
∴a⊥α′，这样平面α与α′都是过点P与直线a垂直的平面．这是一个错误的结论，因此，假设不成立，故必有lÌα，也就是说过点P与a垂直的直线均在平面α内，于是本题获证．
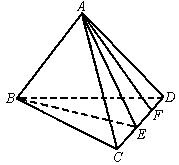
20．证明：先证必要性：过B作CD的垂线，垂足E，连AE，
∵CD⊥AB，
∴CD⊥平面ABE，
∴CD⊥AE．
∴AC2＝AE2＋CE2、BD2＝BE2＋DE2；
又有AD2＝AE2＋DE2、BC2＝BE2＋CE2．
∴AC2＋BD2＝AE2＋BE2＋CE2＋DE2，
而AD2＋BC2＝AE2＋BE2＋CE2＋DE2．
∴AC2＋BD2＝AD2＋BC2．
再证充分性：过A点作CD的垂线，垂足设为F，于是有：
AD2＝AF2＋DF2、BC2＝BE2＋CE2；
AC2＝AF2＋CF2、BD2＝BE2＋DE2；
∵AD2＋BC2＝AC2＋BD2；
∴AF2＋DF2＋BE2＋CE2＝AF2＋CF2＋BE2＋DE2
∴DF2＋CE2＝CF2＋DE2，
∴DF2―CF2＝DE2―CE2，
∴（DF＋CF）（DF－CF）＝（DE＋CE）（DE－CE），
∴DF－CF＝DE－CE．
∴DF＋CE＝DE＋CF．
∴E、F只能重合于一点，故有CD⊥平面ABE，
∴CD⊥AB．
四、思考题
我们称：三对对棱分别互相垂直的四面体为对棱垂直的四面体．
可以证明：对棱垂直的四面体的四条高线相交于一点，反过来，若一个四面体，若它的四条高线相交于一点，则该四面体一定是对棱垂直的四面体．