直线与平面平行的判定与性质
一、选择题
1．已知直线a∥平面α，直线bÌα，则a与b的关系为（ ）
A．相交 B．平行 C．异面 D．平行或异面
2．平面α∩平面β＝a，平面β∩平面γ＝b，平面γ∩平面a＝c，若a∥b，则c与a，b的位置关系是（ ）
A．c与a，b都异面 B．c与a，b都相交
C．c至少与a，b中的一条相交 D．c与a，b都平行
3．给出下列四个命题：
①如果a，b是两条直线，且a∥b，那么a平行于经过b的任何平面；
②如果直线a和平面α满足a∥α，那么a与平面α内的直线不是平行就是异面，
③如果直线a∥α，b∥α，则a∥b
④如果平面α∩平面β＝a，若b∥α，b∥β，则a∥b
其中为真命题有（ ）
A．1个 B．2个 C．3个 D．4个
4．A、B是不在直线l上的两点，则过点A、B且与直线l平行的平面的个数是 （ ）
A．0个 B．1个
C．无数个 D．以上三种情况均有可能
二、填空题
5．在△ABC中，AB＝5，AC＝7，∠A＝60°，G是重心，过G的平面α与BC平行，AB∩α＝M，AC∩α＝N，则MN___________
6．P是边长为8的正方形ABCD所在平面外的一点，且PA＝PB＝PC＝PD＝8，M、N分别在PA、BD上，且
，则MN＝_________．
7．三个平面两两相交，有三条交线，则这三条交线的位置关系为__________．
三、解答题
8．如图，两个全等正方形ABCD与ABEF所在平面相交于AB，ME∈AC，NE∈FB，且AM＝FN，求证：MN∥平面BCE．
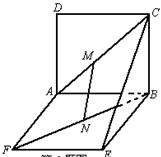
9．求证：如果两个相交平面分别经过两条平行线中的一条，那么它们的交线和这两条平行线互相平行．
10．已知E，F，G，M分别是四面体的棱AD，CD，BD，BC的中点，求证：AM∥平面EFG．
11．在正方体ABCD—A1B1C1D1中，E，F分别是棱BC，C1D1的中点，求证；EF∥平面BB1D1D．
12．空间四边形ABCD的对棱AD，BC成60°的角，且AD＝BC＝a，平行于AD与BC的截面分别交AB，AC，CD，BD于E、F、G、H．
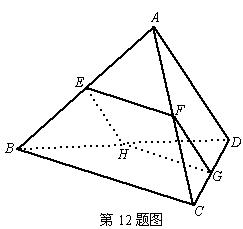
（1）求证：四边形EFGH为平行四边形；
（2）E在AB的何处时截面EFGH的面积最大?最大面积是多少?
参考答案
一、选择题
1．D 2．D 3．B 4．D
二、填空题
5．
；6．
；7．两两平行或相交于一点．
三、解答题
8．证明：过M在平面AC内作直线AB的平行线交于BC于G，过N在平面AE内作直线AB的平行线交BE于H，连GH，只要证明GH∥MN即可，事实上，
∵MG∥AB，NH∥AB，
∴MG∥NH．
又∵
＝
，
＝
，且ABCD和ABEF是两个全等的正方形，AM＝FN，∴AC＝BF，MC＝BN，从而有＝，
∴MG＝NH，∴四边形MGHN为平行四边形．
∴MN∥GH．又∵GHÌ平面BCE，MNË平面BCE，∴MN∥平面BCE．
9．证明：∵a∥b，bÌβ，∴a∥β．
又∵aÌα，α∩β＝l，∴a∥l．
又∵a∥b，b∥l，∴a∥b∥l．
10．证明：连MD交GF于N，连EN．∵GF为△BCD的中位线，
∴N为MD的中点．∵E为AD的中点，
∴EN为△AMD的中位线，∴EN∥AM．
∵AMË平面EFG，ENÌ平面EFG，∴AM∥平面EFG．
11．证明：取D1B1的中点O，连OF，OB．
∵OF
B1C1，BEB1C1，
∵OFBE，则OFEB为平行四边形．
∴EF∥BO．∵EFË平面BB1D1D，BOÌ平面BB1D1D，
∴EF∥平面BB1D1D．
12．证明：（1）∵BC∥平面EFGH，BCÌ平面ABC，平面ABC∩平面EFGH＝EF，
∴BC∥EF，同理BC∥HC，∴EF∥HG．
同理可证EH∥FG，∴四边形EFGH为平行四边形．
解：（2）∵AD与BC成角为60°，
∴∠HEF＝60°（或120°），设
＝x，
∵
＝＝x，BC＝a，
∴EF＝ax，由
＝
＝
，得EH＝（1－x）a．
∴S四边形EFGH＝EF·EH·sin60°
＝ax·a（1－x）·
＝
·x（1－x）≤·
＝
．
当且仅当x＝1－x，即x＝时等号成立，即E为AB的中点时，截面EFGH的面积最大为．