姓名:_______ 班级:______班
_____考室;考号:_____________ 号 高一下册第一次月考数学试卷(测验内容:必修四 P1--92)
一、选择题:(5×10=50′)
1、式子![]() 的值等于: A.
的值等于: A.![]() B.
B. ![]() C.-
C.- ![]() D.-
D.- ![]()
2.把![]() 表示成
表示成![]() (k∈Z)的形式,其中使
(k∈Z)的形式,其中使![]() 最小的值是:
最小的值是:
A.-1350 B.-450 C.450 D.1350
3.在直角坐标系中,角![]() 与角
与角![]() 的终边关于y轴对称,则下列等式恒成立的是:
的终边关于y轴对称,则下列等式恒成立的是:
A、![]() B、
B、![]()
C、![]() D、
D、![]()
4.设O是正方形ABCD的中心,则向量![]() 、
、![]() 、
、![]() 、
、![]() 是:
是:
A.平行向量 B.有相同终点的向量 C.相等的向量 D.模都相同的向量
5.函数y=sin(2x + ![]() )的一条对称轴为:A.x=
)的一条对称轴为:A.x=![]() B.x= 0
C.x=-
B.x= 0
C.x=-![]() D.x =
D.x =![]()
6.为了得到函数![]() 的图象,只需把函数
的图象,只需把函数![]() 的图象:
的图象:
A.向左平行移动![]() 个单位长度
B.向右平行移动
个单位长度
B.向右平行移动![]() 个单位长度
个单位长度
C.向左平行移动![]() 个单位长度
D.向右平行移动
个单位长度
D.向右平行移动![]() 个单位长度
个单位长度
7.已知函数![]() ,则有:
,则有:
A.![]() 与
与![]() 都是奇函数
B.
都是奇函数
B.![]() 与
与![]() 都是偶函数
都是偶函数
C.![]() 是奇函数,
是奇函数,![]() 是偶函数 D.
是偶函数 D.![]() 是偶函数,
是偶函数,![]() 是奇函数
是奇函数
8. 若![]() 是第四象限角,则
是第四象限角,则![]() 是:
是:
A![]() 第一象限角
B
第一象限角
B![]() 第二象限角
C
第二象限角
C![]() 第三象限角
D
第三象限角
D![]() 第四象限角
第四象限角
9、已知集合![]() ,则:
,则:
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
10、设![]() 是定义域为R,最小正周期为
是定义域为R,最小正周期为![]() 的函数,若
的函数,若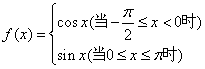 ,则
,则![]() 的值等于:
的值等于:
A.![]() B.
B.![]() C.0
D.
C.0
D. ![]()
二、填空题(5*5=25分):
11、在平行四边形![]() 中,设
中,设![]() 为
为![]() 上任一点,则
上任一点,则![]() _______
_______
12、.函数![]() 的最大值是
的最大值是![]() ,最小值是
,最小值是![]() ,则
,则![]() =______,
=______, ![]() =______.
=______.
13、一艘船从某个地点出发,以2km/h的速度向垂直于对岸的方向行驶,同时河水的流速为2km/h;则船实际航行的速度大小为________km/h;其方向是与水流方向成多少度角_________。
14、已知函数![]() ,若对任意
,若对任意![]() 都有
都有![]() 成立,则
成立,则![]() 的最小值是______________.
的最小值是______________.
15、当![]() 时,函数
时,函数![]() 的值域为_______________
的值域为_______________
(一)选择题答案:
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
(二)填空题答案:
11题:_______; 12题:______ ______; 13题:____ ______; 14题:_________; 15题:__________
三、解答题(共75分):
16题(12分).(1)(6分)、化简: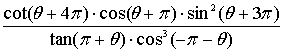
(2)(6分)、若![]() ,求
,求![]() 之值
之值
17题(12分)、求证:![]()
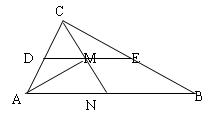 18题:(6+6=12分)、如图,在
18题:(6+6=12分)、如图,在![]() 中,D、E分别是AC、BC的中点,M是DE的中点,若
中,D、E分别是AC、BC的中点,M是DE的中点,若![]() . (1)用
. (1)用![]() 表示
表示![]() ;(2)若N为线段AB的中点,求证:C、M、N三点共线.
;(2)若N为线段AB的中点,求证:C、M、N三点共线.
19题(5+4+5=14分)、.已知函数![]() 。
。
(1)求函数y的最大值及y取最大值时x的集合;(2)求函数y的单调递减区间;
(3)将函数![]() 的图象作怎样的变换可得到
的图象作怎样的变换可得到![]() 的图象?
的图象?
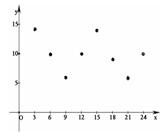
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.4 | 1.0 |
20题(3+5+5=13分)、某“海之旅”表演队在一海滨区域进行集训,该海滨区域的海浪高度y(米)随着时间t(0≤t≤24,单位:小时)而周期性变化.;为了了解变化规律,该队观察若干天后,得到每天各时刻t的浪高数据的平均值如下表:
(1)试画出散点图;(2)观察散点图,从![]() 、
、![]() 、
、![]() 中选择一个合适的函数模型,并求出该拟合模型的解析式;(3)如果确定当浪高不低于0.8米时才进行训练,试安排白天内进行训练的具体时间段.
中选择一个合适的函数模型,并求出该拟合模型的解析式;(3)如果确定当浪高不低于0.8米时才进行训练,试安排白天内进行训练的具体时间段.
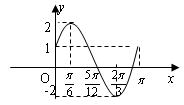
21题(5+7=12分):已知函数![]() 在一个周期内的图象如所示。
在一个周期内的图象如所示。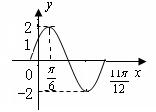
(1)求函数的解析式; (2)设![]() ,且方程
,且方程![]() 有两个不同的实数根,求实数m的取值范围以及这两个根的和。
有两个不同的实数根,求实数m的取值范围以及这两个根的和。
参考答案:
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | A | C | D | D | C | D | C | B | B |
11题: ![]() 12题: 1 ; 13题:; 4km/h,60° 14题:
2;
15题:
[,2]
12题: 1 ; 13题:; 4km/h,60° 14题:
2;
15题:
[,2]
16题. (1)、1 (2)解:原式![]() 17题、证明:左边=
17题、证明:左边=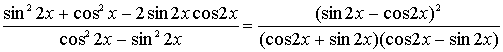
![]()
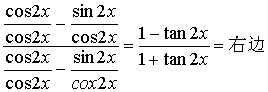
18题、(1)![]() .
.
(2)![]()
![]() ,
,![]()
![]()
![]() ,即C、M、N三点共线。
,即C、M、N三点共线。
19题、(1)当![]() 时,y取最大值
时,y取最大值![]() ,此时
,此时![]()
 即
即![]() ;
;![]() 取最大值1时,x的集合为
取最大值1时,x的集合为![]() ;(2)原函数的单调递减区间为:
;(2)原函数的单调递减区间为:![]() ;(3)法一:将
;(3)法一:将![]() 的图象的横坐标变为原来的
的图象的横坐标变为原来的![]() ,再将所得图象向右平移
,再将所得图象向右平移![]() 个单位。 法二:将
个单位。 法二:将![]() 的图象向右平移
的图象向右平移![]() 个单位,再将所得图象的横坐标变为原来的
个单位,再将所得图象的横坐标变为原来的![]() 。 20题、由散点图可知,选择
。 20题、由散点图可知,选择![]() 函数模型较为合适.由图可知,
函数模型较为合适.由图可知,
![]() (0≤t≤24)(3)由
(0≤t≤24)(3)由![]() (0≤t≤24),即
(0≤t≤24),即![]() . 则
. 则![]() ,得
,得![]() 从而
从而 ![]() 或
或![]() 或
或![]() .所以,应在白天11时~19时进行训练. 21(1)所求的函数的解析式为:
.所以,应在白天11时~19时进行训练. 21(1)所求的函数的解析式为:![]() .(2)在同一坐标系中画出
.(2)在同一坐标系中画出![]() 和
和![]() (
(![]() )的图象,由图可知,当
)的图象,由图可知,当![]() 时,直线
时,直线![]() 与曲线有两个不同的交点,即原方程有两个不同的实数根。
与曲线有两个不同的交点,即原方程有两个不同的实数根。 ![]() m的取值范围为:
m的取值范围为:![]() ; 当
; 当![]() 时,两根和为
时,两根和为![]() ;当
;当![]() 时,两根和为
时,两根和为![]() .
.