姓名：_______ 班级： ____班
_____考室；考号： _____________ 号 中 考 数 学 试 卷 (测验内容：必修四全部)
撰稿： 方锦昌 电子邮箱 fangjingchang2 手机号码
一、选择题：(5×10=50′)
1、已知
=（
，
），
=（
，
），且∥，则有：
A、+=0， B、―=0， C、+=0， D、―=0，
2.、函数
的周期为： A. 
B. 
C.
D.
3、若
，则
等于：
A.
B.
C.
D. 
4．在锐角△ABC中，设
则x与y的大小关系为：
（A）
（B）
（C）
（D）
5、要得到函数
的图象；只需将函数y=3sin2x的图象：
A．向左平移
个单位；B．向右平移个单位；C．向左平移
个单位；D．向右平移个单位
6、化简
的所得结果是：
A．
B．
C．
D．无法确定
7、函数
的定义域是：
A．
B．
C．
D．
8、设
为三角形ABC的一个内角,若
,则这个三角形的形状为 ：
A. 锐角三角形 B. 钝角三角形 C. 等腰直角三角形 D. 等腰三角形
9、向量
满足
，则
的夹角等于：
A．
B 
C 
D 
 |
10、函数
的部分图象是：
二、填空题（25分）
11、已知向量
＝（4，2），向量
＝（
，3），且//,则＝
12、已知
则
13．若
，则
= ；
14、向量、满足
=
=1，
=3，则
=
15、已知a=1,b=2,a与b的夹角为60°，c=2a+3b,d=ka-b(k∈R)，且c⊥d，那么k的值为 _____
一、选择题答案:
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题答案：11题_______; 12题________; 13题________; 14题_______; 15题_________
.三、解答题：
16题(6+6=12分)、（1）、求值
（2）、化简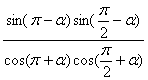
17题(6+6=12分)、已知函数
，
。
（1）、当函数
取得最大值时，求自变量
的集合；（II）该函数的图象可由
的图象经过怎样的平移和伸缩变换得到？
18题(6+6=12分)、设点A（2，2），B（5，4），O为坐标原点，点P满足
=
+
，（t为实数）；
（1）、当点P在x轴上时，求实数t的值； （2）、四边形OABP能否是平行四边形？若是，求实数t的值 ；若不是，请说明理由，
19题(4+4+5=13分)、已知向量
，且
，求：
（1）
及
；（2）若
的最小值为
，求实数
的值。
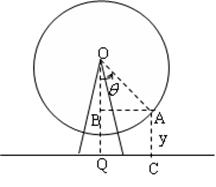
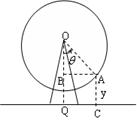
20题(4+4+5=13分)、如图，游乐场所的摩天轮匀速旋转，每转一周需要12min，其中心O离地面45米，半径40米.如果你从最低处登上摩天轮，那么你与地面的距离将随时间的变化而变化，以你登上摩天轮的时刻开始计时，请回答下列问题：
（1）求出你与地面的距离
和时间
(min)的函数关系式；
（2）当你第四次距离地面65米时，用了多少时间？
（3）当你登上摩天轮2分钟后，你的朋友也在摩天轮的最低处登上摩天轮，问你的朋友登上摩天轮多少时间后，第一次出现你和你的朋友与地面的距离之差最大？求出这个最大值。
21题(6+7=13分)、已知函数f(x)=A
(A>0,
>0,0<
<
函数，且y=f(x)的最大值为2，其图象相邻两对称轴间的距离为2，并过点（1，2）；
（1）求之值; （2）计算f(1) + f(2)
+ …… + f(2 008)之值.
中考数学参考答案：
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | A | B | B | C | B | D | B | A | D |
11题：6; 12题：
; 13题：－3 _; 14题：2
；; 15题：
16题、 （1）、
（2）、
17题、解：（I）、
， 所求
。
18题、解：（1）、设点P（x，0）， 
=(3,2), ∵=+，∴ (x,0)=(2,2)+t(3,2),
∴ 
(2)、设点P（x,y），假设四边形OABP是平行四边形，
则有∥
, Þ y=x―1, ∥ Þ2y=3x 
…… ①, 又由=+，Þ (x,y)=(2,2)+ t(3,2),得 ∴ 
……
②, 由①代入②得：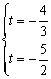
， 矛盾，∴假设是错误的， ∴四边形OABP不是平行四边形。
19题、解：（1）
又
从而
（2）
由于 故
①当
时，当且仅当
时，
取得最小值
，这与题设矛盾；②当
时，当且仅当
时，取得最小值
，由
及得
；③当
时，当且仅当
时，取得最小值
，由
，得
与矛盾；
综上所述，即为所求。
20题、解：（1）
摩天轮的角速度
最低点的角终边OQ到与地面的距离的角终边OA的角
，
，即与地面的距离与时间(min)的函数关系式为 
；
（2）令
得
，第四次距离地面65米，即为第2周的第二次，
，
，即第四次距离地面65米时，用时20min.
(3)当朋友距离地面高度
时，这时自己距离地面高度
；
当两人所处位置连线垂直地面时，距离之差最大，这t=2.即当你的朋友登上摩天轮2min后，第一次出现你和你的朋友与地面的距离之差最大；这个最大值为40m。
(因为：
=
=
=
)
21题、
，
.
又
的周期为4，
，