高一数学第二学期第二次四校联考试卷
一、选择题:(每小题5分,共60分)
1.若![]() 是不共线的任意三点,则下列各式中成立的是( )
是不共线的任意三点,则下列各式中成立的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
2.函数![]() 是( )
是( )
A、周期为![]() 的奇函数
B、周期为
的奇函数
B、周期为![]() 的偶函数
的偶函数
C、周期为![]() 的奇函数
D、周期为
的奇函数
D、周期为![]() 的偶函数
的偶函数
3.若![]() 是
是![]() 的一个内角,且
的一个内角,且![]() 则
则![]() 等于( )
等于( )
A、![]() B、
B、![]()
C、![]() 或
或![]() D、
D、![]() 或
或![]()
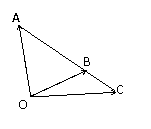 4.如图所示,向量
4.如图所示,向量![]()
A、B、C在一条直线上,且![]() ,则( )
,则( )
A、![]()
B、![]()
C、![]()
D、![]()
5.![]() 是夹角为
是夹角为![]() 的两个单位向量,则
的两个单位向量,则![]() 等于( )
等于( )
A、![]() B、
B、![]() C、
C、![]() D、8
D、8
6.若![]()
![]() 共线,且
共线,且![]() 则
则![]() 等于_______
等于_______
A、1 B、2 C、3 D、4
7.与向量![]() 垂直的单位向量是( )
垂直的单位向量是( )
A、![]() B、
B、![]()
C、(![]() 或
或![]() D、
D、![]() 或
或![]()
8.已知![]()
![]()
![]() ,则
,则![]() 是( )
是( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、任意三角形
9.函数![]() 的单调递增区间为( )
的单调递增区间为( )
A、![]()
B、![]()
C、![]()
D、![]()
10.已知![]() ,
,![]() 在
在![]() 方向上的投影是
方向上的投影是![]() ,则
,则![]() 是( )
是( )
A、3 B、![]() C、2
D、
C、2
D、![]()
11.若![]() ,则( )
,则( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
12.已知点![]() ,函数
,函数![]() 的图象与线段
的图象与线段![]()
![]() 的交点
的交点![]() 分有向线段
分有向线段![]() 的比为3:2,则
的比为3:2,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、4
D、4
二、填空题:(每题5分,共20分)
13.![]() ______________。
______________。
14.已知![]()
![]() ,且
,且![]() 与
与![]() 的夹角为锐角,则
的夹角为锐角,则![]() 的取值范围是______________________。
的取值范围是______________________。
15.已知![]() 的顶点
的顶点![]() 和重心
和重心![]() ,则
,则![]() 边的中点坐标是_________________。
边的中点坐标是_________________。
16.关于函数![]() 有下列命题:
有下列命题:
①由![]() 可得
可得![]() 必是
必是![]() 的整数倍
的整数倍
②由![]() 的表达式可改写为
的表达式可改写为![]()
③![]() 的图像关于点
的图像关于点![]() 对称
对称
④![]() 的图象关于直线
的图象关于直线![]() 对称
对称
其中正确命题的序号是____________________。
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
答题卷
一、选择题:请将唯一正确答案的编号填入答卷中,本题共12题,每题5分,共60分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、 填空题:本题共4题,每题5分,共20分。
13、_________________________ 14、_________________________
15、_________________________ 16、_________________________
三、解答题(共70分)
17、(10分)已知![]() ,
,![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() 。
。
求(1)![]() .
(2)
.
(2)![]()
18.(12分)已知![]() 若
若![]() ,
,![]() 在直线
在直线![]() 上, 求
上, 求![]() 的坐标。
的坐标。
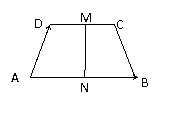 19、(12分)如图:梯形ABCD中,AB//CD,且AB=2CD,M、N是DC、BA的中点,设
19、(12分)如图:梯形ABCD中,AB//CD,且AB=2CD,M、N是DC、BA的中点,设![]() ,
,![]() ,试以
,试以![]() 、
、![]() 为基底表示
为基底表示![]() 、
、![]() 。
。
20、(12分)已知![]() ,
,![]() ,
,![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中![]() ,
,![]() 且
且![]() 与
与![]() 垂直,求
垂直,求![]() 与
与![]() 的夹角
的夹角![]() 。
。
21.(12分)已知函数![]()
⑴求![]() 的最大值和最小值。
的最大值和最小值。
⑵若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围。
的取值范围。
 22、(12分)已知函数
22、(12分)已知函数![]()
(1)求![]() 的定义域G;
的定义域G;
(2)用定义判断![]() 的奇偶性;
的奇偶性;
(3)在![]() 上作出函数
上作出函数![]() 的图象;
的图象;
(4)指出函数![]() 的最小正周期及单调递增区间。
的最小正周期及单调递增区间。
参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | C | A | C | B | D | B | C | B | A | D |
13、![]() 14、
14、![]()
15、![]() 16、②③
16、②③
17、解:![]()
⑴![]()
![]() ┄┄┄┄┄5分
┄┄┄┄┄5分
⑵![]()
![]() ┄┄┄┄┄10分
┄┄┄┄┄10分
18、解:由条件得 ![]() 或
或 ![]()
⑴当![]() 时
时 ![]()
设![]() 则
则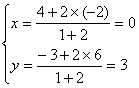
∴![]() ----------5分
----------5分
⑵当![]() 时
时 ![]()
则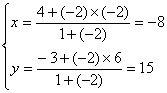 ∴
∴![]() -----10分
-----10分
![]() 点的坐标为
点的坐标为![]() 或(-8,15) -----------12分
或(-8,15) -----------12分
19、解:∵![]() ∥
∥![]() 且
且![]()
∴![]() -------------2分
-------------2分
又 ![]()
∴![]() ------------6分
------------6分
又 ![]()
∴![]() ------------9分
------------9分
过D作DE∥MN,则E为AN中点
∴![]()
∴![]() ------------12分
------------12分
20、解:⑴∵![]()
![]()
∴![]()
![]() ------------2分
------------2分
∴2![]() ------------4分
------------4分
![]() -------6分
-------6分
∴![]() -----------8分
-----------8分
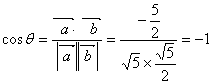 -----------10分
-----------10分
而 ![]() ∴
∴![]() -----------12分
-----------12分
21、解:⑴![]()
![]()
![]() -----------4分
-----------4分
又 ∵![]() ∴
∴![]()
∴![]()
∴![]() ------------8分
------------8分
⑵ ∵![]() 在
在![]() 上恒成立
上恒成立
∴![]()
∴![]() 且
且 ![]() -----------10分
-----------10分
即 ![]() 且
且 ![]()
∴![]() -----------12分
-----------12分
22、解:⑴ 由 ![]() 得
得 ![]()
![]()
∴![]() 的定义域为
的定义域为![]() --------3分
--------3分
⑵∵ 定义域关于原点对称,对任意![]()
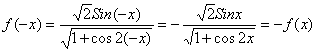
∴![]() 是奇函数
---------6分
是奇函数
---------6分
⑶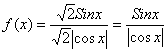 又
又 ![]() 且
且![]()
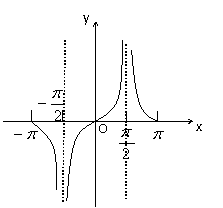 ∴
∴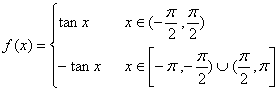
![]() 的图象如图所示:
--- 10分
的图象如图所示:
--- 10分
⑷由图可见![]() 的最小正周期为
的最小正周期为![]()
![]() 的单调增区间为
的单调增区间为 ![]() --------12分
--------12分