高一数学第二学期第二次月考试卷
本试题分Ⅰ卷（选择题）和Ⅱ卷两部分。考试结束后，将答题卡和Ⅱ卷答题纸上交。本试卷共150分，考试时间为120分钟。
第Ⅰ卷
一、选择题（每小题5分，共65 分）
1．
的值是 ( )
A. 
B.
C. 
D. 
2．时钟的分针经过40分钟时间旋转的角度是 ( )
A. 
B. 
C. 
D. 
3.
已知
，则
的值是 ( )
A．
B．
C．2 D．－2
4．
( )
A．
B． C．
D．
5．若
，且
， 则 ( )
A．
B．
C．
D．
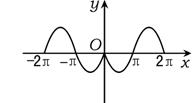6．与图中曲线对应的函数是 ( )
A. y=sinx B. y=sinx
C. y= - sinx D.y= - sinx
7. (1+tan25°)(1+tan200°)的值是( )
A . 2 B. -2 C. 1 D. -1
8.下列命题是真命题的是：①
存在唯一的实数
，使
；②存在不全为零的实数
，使
；③
与
不共线
若存在实数，使，则
；④与不共线不存在实数使．( )
A．①和③ B．②和③ C．①和② D． ③和④
9．已知 
则 
的取值范围是 ( )
A．[3，17] B．（3，17） C．[3，10 ] D．（3，10）
10．函数f（x）=cos(3x+φ)的图像关于原点中心对称的充要条件是（ ）
A. φ= B. φ= kπ+ (k∈Z)
C. φ= kπ (k∈Z) D. φ= 2kπ- (k∈Z)
11．为了得到函数
的图象，可以将函数
的图象（ ）
A．向右平移
个单位长度
B．向右平移
个单位长度
C．向左平移个单位长度
D．向左平移个单位长度
12．把函数y=sin(2x+
)的图象向右平移
(>0)个单位，所得的图象关于y轴对称，则的最小值是 ( )
A.
B.
C.
D.
13．已知关于
的方程
在区间
内有解，则实数
的取值范围是
(
)
A．
B．
C．
D．
二、填空题（每小题5分，共25 分）
14．函数y=sin(3x-)
的周期是
，振幅是 ，频率是
，初相是_________．
15．
，
是两个不共线的向量，已知
，
，
且
三点共线，则实数
=
16．在
中，点
，
，
分别是
，
，
的中点，
则
．
17．若tan
=2，则2sin2－3sincos=
。
18．若
－
，∈（0，π），则tan=
。
三、解答题 （共5题，每题12分，共60分）
19．已知角
是第三象限角，且
（1）化简
；
（2）若
，求的值；
（3）若
，求的值
20．已知函数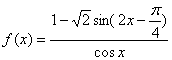
（1）求
的定义域；
（2）设是第四象限角，且
，求的值。
21．设
，
，且
，
，
求
的值．
22．已知函数f(x)=Asin
的图像与y轴上的截距为1，在相邻两最值点
上
分别取得最大值和最小值.
(1)求的解析式;
(2)在区间
上是否存在的对称轴？请说明理由。
23． 已知定义在R上的函数
的周期为
，
，且的最大值为2。
（1）写出的表达式；
（2）写出函数的周期、对称中心、对称轴方程；
（3）说明的图象如何由函数
的图象经过怎样的变换得到。
参考答案
一、选择题（每小题5分，共65 分）
ADABC CABAB BBA
二、填空题：（每小题5分，共25 分）
14.
15.
16.
17. 
18. 
或
三、解答题:(共60分)
19.(1) =
(2) 
(3) 
20.（1）{
} (2)
21.
22.（1）
这时
（2）
故
即在上不存在
23. 解：（1）
（2）
，对称中心（
，0）对称轴
（3）将函数y=2sinx的图象向左平移个单位，再将得到的函数图象上的所有的点的纵坐标不变，横坐标缩短为原来的