高一数学第二学期调研考试试题

高一数学第二学期调研考试试题

　命题人：房国新　　 2008.03.10

一、填空题（每题5分共70分）

1．的内角的对边分别为，若

则=___________

2．等差数列中，，，那么　　　　。

3．已知数列的，则=_____________。

4．公差不为0的等差数列中，依次成等比数列，则此公比等于　　　

5．在正实数组成的等比数列中，若，

则＝　　　。

6．的内角的对边分别为，若成等比数列，且，

则　　　　　　

7．数列中，，，则通项　　　　　　 。

8．求数列前n项和　　　　　　 。

9．已知数列中，，且是递增数列，求实数的取值范围　　　　　　 

10．数列，，，，，……的前n项和=　　　　　　　　。

11．已知数列满足.

若，则_____________.

12．设函数f（x）满足 =（n∈N^*）且，则 =　　　　 。 13．的内角的对边分别为，若，，则的取值范围是　　　　　　　　　　 

14. 把数列中各项划分为：（3），（5，7）, (9,11,13) ,　(15,17,19,21) ,　(23) , (25,27)，(29,31,33) , (35,37,39,41),照此下去，第100个括号里各数的和为　　　　　 

二　解答题（15题、16题、17题、18题均14分，19题16分，20题18分）

15．的内角的对边分别为，若，且

求和

16．设数列是公差不为0的等差数列，它的前10项和，

且成等比数列。

（1）求数列的通项公式；

（2）设，求数列的前项和。

17．在等比数列中，，公比， ， 且是与的等比中项，

（1）求数列的通项公式；

（2）设，数列的前项和为，当最大时，

求的值.

18．数列中，，，且满足

（1）求数列的通项公式；

（2）设，求。

19．已知数列满足

　 （1）求证：为等比数列；

　 （2）记为数列的前项和， 当时，求 。

20．已知数列中，，．

　（1）求；

　（2）求数列的通项；

　（3）设数列满足，求证：

 

 

高一数学试题参考答案

一．　　　　　 填空题：（每题5分共70分）

1．　2　　　　　　　　　　　 　　　 2．　　0　　　　　　　　

3．　 54　　　　　　　　　　  　　　 4．　　 3　　　　　　　 

5．　3　　　　　　　　　　　 　　　 6．　　3/4　　　　　　　　

7．　　　　　　　　　8．　　　 n/(n+2)　　　　　　 

9．　　 a>1/3　　　　　　　　　  　　　 10．　 　

11．　　4012　　　　　　　　　  　　　12．　　 97　　　　　　　 

13．　　 　　　　　　　　　　　　　14．　　 1992　　　 　

二．解答题（15题、16题、17题、18题均14分，19题16分，20题18分）

15． 的内角的对边分别为，若，且

求和

解：因为得

又因为--------------------------------------4

所以

所以-------------------------------------------------------------------------------- 8

因为得----------------------------------10

所以

------------------------------------12

得

所以---------------------------------------------------------------------------------14

16．解：（1）因为成等比数列。所以得-----------------------3

由得-----------------------------------------------------------------------6

所以---------------------------------------------------------------------------------10

（2）-------------------------------------------------------------12

所以--------------------------14

17．解：（1）由得得

　 因为得-----------------------------------------4

　求得

所以----------------------------------------------------------------------------------------8

（2）-----------------------------------------------10

所以-----------------------------------------------------11

---------------------------------------------------------12

所以最大为------------------------------14

18．解：（1）∴

∴为常数列，∴{a_n}是以为首项的等差数列，------4

∴。----------------------------------------8

（2）∵，

设，求得-----------------------------10

∴当时，

=----------------------------------------------------------12

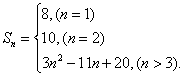∴----------------------------------------------14

19．解：1）当n≥2时，

整理得

所以{a_n}是公比为a的等比数列. ------------------------------------------------------　8

（2）

------------------------------------------------10

当a=2时，

---------------------------------------12

两式相减，得

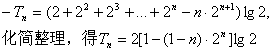  ----------------------------------------------16

20．解：（1）_{----------------------------------------------------------3}

（2）　　　　　 ①

　　　　②

①—②得

即：，_{---------------------------------------------6}

所以

所以_{------------------------------------------------------------------10}

（3）由（2）得：，

所以是单调递增数列，故要证：只需证

若，则显然成立

若，则

所以_{------------------------------------------------------------------14}

因此：

所以

所以_{-------------------------------------------------------------------18}