高一数学第二次月考试题
一、填空题(本大题共70分，每小题5分)
1、数列
的一个通项公式为
______________
2、数列
中，
，
，则
______________4
3、等差数列
中, 
则公差
______________
2
4、等比数列中, 
则
=___________96
5、
与
的等差中项是___________
6、等比数列中, 
则的前
项和等于___________120
7、等差数列中, 
则
_________ 4
8、等比数列中，任意的
，有
，
，
则___________5
9、等差数列
项的和
等于___________99
10、函数
的定义域为___________
11、数列的前项和
，
则
_________
12、已知两个等差数列和
的前项的和分别为
和
，且
，则使得
为整数的正整数有_________个5
13、数列中，
，
，
，
则
_________7
14、将正整数按下表的规律排列，把行与列交叉处的一个数称为某行某列的数，记作
，如第2行第4列的数是15，记作
，则
________________.280
1 4 5 16 17 36 …
2 3 6 15 18 35 …
9 8 7 14 19 34 …
10 11 12 13 20 33 …
25 24 23 22 21 32 …
26 27 28 29 30 31 …
… … … … … … …
二、解答题（本大题共90分）
15、（本小题14分）成等差数列的四个数的和为
，第二数与第三数之积为
，求这四个数
解：设四数为
，则
即
，
当
时，四数为
当
时，四数为
16、（本小题14分）函数
，
（1）求
的值
（2）求
的解集
（1）2
（2）
17、（本小题14分）在等比数列
中，
（1）求
的值
（2）求
和
的值
（3）若
求的取值范围
解：（1）
（2）
当
时，
；
当
时，
；
（3）当时，，
当时，；
为偶数
∴
18、（本小题18分）已知数列
的通项公式
，
（1）若
，求此时的值
（2）
，求数列
的前项和的表达式
(3) 
,求数列
的前项和
的表达式
解：（1）
（2）
，当
时，
当
时，
∴
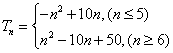
（3）
19、（本小题15分）某企业年初有资金1000万元，如果该企业经过生产经营能使年资金平均增长率达到50%，但每年年底都要扣除消费基金x万元，余下的投入再生产，为实现经过10年资金达到3000万元，（扣除消费基金后）求每年应扣除消费基金多少万元？（结果精确到1万元）
（参考数据：
）
482.4
482
20、（本小题15分）已知一个数列{an}的各项是1或3．首项为1，且在第k个1和第k+1个1之间有2k-1个3，即1，3，1，3，3，3，1，3，3，3，3，3，1，…，记该数列的前n项的和为Sn．
（1）试问第2008个1为该数列的第几项？
（2）求a2008；
（3）求该数列的前2008项的和S2008；
(1) (2)3 (3)5934