高一数学集合单元测试试题

姓名_______　　　　　　　　　　　 

学号________　　　　　　　　　　 高一数学集合单元测试试题（1）

班级_________　　　　　　　　　　 

　　　　　　　　　　  撰稿： 方锦昌  电子邮箱 fangjingchang2 　　 手机号码

一、选择题（每小题5分，共50分）(选择题的答案请全部填写在第10题后的表格之中)

★1．已知全集,，则(　　)

A. 　　　　　 B. 　　　　C. 　　　　 D.

★2．已知集合(　　 )

. A. {x2<x<3}　　　　B. {x-1≤x≤5}　　　　  C. {x -1<x<5}　　　　　  D.{x -1<x≤5}

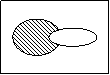★3．图中阴影部分表示的集合是(　　 )

　　 A. A∩C_UB 　　　B.C_UA∩B 

C.C_U(A∩B)　　 D. CU(A∪B)

★4．方程组的解集是（　　 ）

A . 　　　　 B. 　　　　 C. 　　　　　 D.

★5．已知集合, 则A与B之间最适合的关系是（　　 ）

A.、　　 　 B.、　　　　 C、AÜB.　　　　　  D.、AÝB

★6．（07江西）若集合M＝{0，l，2}，N＝{(x，y)x－2y＋1≥0且x－2y－1≤0，x，y ∈M}，则N中元素的个数为（　）

　　　　A．9　　　　　　 B．6　　　　　　 C．4　　　　　　　 D．2　　　　 C.

★7．（07湖北）集合P＝｛x」x²－16<0｝,Q＝｛x」x＝2n，nZ｝,则P∩Q＝（　　）

A.｛-2,2｝　　 B.｛－2，2，－4，4｝　　 C.｛-2，0，2｝　　  D.｛－2，2，0，－4，4｝

★8．（07江西卷）已知集合M＝｛x｝，N＝｛yy＝3x²＋1，xÎR｝，则MÇN＝（　 ）

A．Æ　 　 B. {xx³1}　　 C.｛xx>1｝ 　　　 D. {x x³1或x<0}

★9、（07辽宁卷）设集合,则满足的集合B的个数是（　 ）

(A)1　 　　　 (B)3  　　　　　(C)4 　　　　　 (D)8

★10、（06湖北卷）有限集合中元素的个数记做，设都为有限集合，给出下列命题：

①的充要条件是；②的必要条件是；③AB的充分条件是；④的充要条件是；其中真命题的序号是（　 ）：A．③④　 　B．①②　　 C．①④　　 D．②③

选择题答案:

1	2	3	4	5	6	7	8	9	10

二、填空题（每小题5分,共25分）

●11.已知集合，写出集合A的所有真子集　　　　

●12. (07重庆卷)已知集合U={1,2,3,4,5,6,7}, A={2,4,5,7},B={3,4,5},则(_uA)∪(_uB)=____

●13. (07上海卷)已知，集合，若,则实数。

●14、(07全国卷I）设集合，，则M∩N= _____　　

●15、已知集合，，若A∩B=Æ，则实数的取值范围是　　　　

.三、解答题（12+12+12+12+13+14，共75分）

★16（12分）、设U={x∈Z0<x≤10},A={1,2,4,5,9},B={4,6,7,8,10},C={3,5,7},求

A∩B,A∪B,(C_UA)∩(C_UB),(C_UA)∪(C_UB),(A∩B)∩C,(A∪B)∩C。

解：①、A∩B=

②、A∪B=

③、(C_UA)∩(C_UB)=

④、(C_UA)∪(C_UB)=

⑤、(A∩B)∩C=

⑥、(A∪B)∩C=

★17（12分）、已知集合，.

（1）当m=3时，求集合A∩B；　　（2）若，求实数m的取值范围.

★18（12分）、已知集合A=｛xx²-2x-8=0｝,B=｛xx²+ax+a²-12=0｝且有A∪B=A ，求实数a的取值集合。

★19（12分）、已知不等式 对于所有的 恒成立，求实数 的取值范围

★20（13分）、已知集合A={（x，y）x²+mx－y+2=0}，B={（x，y）x－y+1=0，0≤x≤2}，如果A∩B≠，求实数m的取值范围.

★　　 21题（14分）、若B={xx²－3x+2＜0}，请问是否存在实数a，使A={xx²－（a+a²）x+a³＜0}满足：A∩B=A？若存在，请求出a相应的取值范围；若不存在，请说明你的理由.

　　　　　　　　　　　　 参考答案

1	2	3	4	5	6	7	8	9	10
C	B	A	C	D	C	C	C	C	B

●11. {a2<a<3}；　●12. {1,2,3,6,7}；　●13. 4　　●14、M∩N=_____　　

●15、略

★16、略；

★17、解: ；　

★18、解：{aa<-4,或a=-2,或a≥4}；

★19、略

★20、

●解：由得x²+（m－1）x+1=0.　①；∵A∩B≠，∴方程①在区间［0，2］上至少有一个实数解.首先，由Δ=（m－1）²－4≥0，得m≥3或m≤－1.

当m≥3时，由x₁+x₂=－（m－1）＜0及x₁x₂=1知，方程①只有负根，不符合要求；

当m≤－1时，由x₁+x₂=－（m－1）＞0及x₁x₂=1＞0知，方程①有两个互为倒数的正根.故必有一根在区间（0，1］内，从而方程①至少有一个根在区间［0，2］内.

综上所述，所求m的取值范围是（－∞，－1］.

★21题、

●解：∵B={x1＜x＜2}，若存在实数a，使A∩B=A，则A={x（x－a）（x－a²）＜0}.

（1）若a=a²，即a=0或a=1时，此时A={x（x－a）²＜0}=，满足A∩B=A，∴a=0或a=1.

（2）若a²＞a，即a＞1或a＜0时，A={x0＜x＜a²}，要使A∩B=A，则1≤

a≤，∴1＜a≤；（3）若a²＜a，即0＜a＜1时，A={xa＜x＜a²}，要使A∩B=A，则1≤a≤2，∴a∈.；

综上所述，当1≤a≤或a=0时满足A∩B=A，即存在实数a，使A={xx²－（a+a²）x+

a³＜0}且A∩B=A成立.