姓名_______ 湖南省省级示范性高中……洞口三中数学教学讲义稿
学号________ 高一《集合》单元测试试题（1）
班级_________ 撰稿： 方锦昌 电子邮箱 fangjingchang2 手机号码
一、选择题：(5×10=50′)
★1．设全集U＝R，集合A＝(1，＋∞)，集合B＝(－∞，2)。则
U(A∩B)＝（ ）
A．(－∞，1)∪(2，＋∞) B．(－∞，1)∪[2，＋∞)
C．(－∞，1]∪[2，＋∞) D．(－∞，1]∪(2，＋∞)
★2、已知A={1，a}，则下列不正确的是（ ）
Ａ：a∈A Ｂ：１∈Ａ Ｃ：（１、a）∈Ａ Ｄ：1≠a
★3、集合
，
，
之间的关系是（ ）
（A）
（B）
（C）
(D)
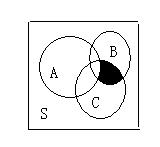
★4、如图，阴影部分所表示的集合为（ ）
A 、A∩（B∩C） B、（CSA）∩（B∩C）
C、（CSA）∪（B∩C） D、（CSA）∪（B∪C）
★5、设I为全集，S1、S2、S3是I 上的三个非空子集，且S1∪S2∪S3=I，则下列 论断正确的是（ ）
A、 CIS1∩（S2∪S3）=Æ B、 S1Í（CIS2∩CIS3）
C、 CIS1∩CIS2∩CIS3=Æ D、 S1Í（CIS2∪CIS3）
★6、设关于x的式子当x∈R时恒有意义，则实数a的取值范围是（ ）
A、a≥0 B、a<0 C、a< D、 a≥0或a<
★7、设集合S=｛a,b,c,d,e｝,则包含｛a,b｝的S的子集共有（ ）个
A 2 B 3 C 5 D 8
★8、设集合M=｛xx= +,k∈Z｝,N=｛xx= +,k∈Z｝,则（ ）
A、 M=N B、 MÜN C、 MÝN D、 M∩N=Æ
★9、设⊕是R上的一个运算,A是R上的非空子集,若对任意的a、b∈A，有a⊕b∈A，则称A对运算⊕封闭，下列数集对加法、减法、乘法和除法（除数不等于0）四则运算都封闭的是（ ）
A 自然数集 B 整数集 C 有理数集 D 无理数集
★10、设P、Q为两个非空实数集合，定义集合P+Q=
，则P+Q中元素的个数是（ ）
A．9 B．8 C．7 D．6
二、 填空题（5×5=25′）
★11、已知集合
，
，若
，则实数
的取值范围是
.
★12、Ａ＝｛a²,a+1,－3｝，Ｂ＝｛a－3,2a－1,a²+1｝，若Ａ∩Ｂ＝｛－３｝，那么a＝_______.
★13、设全集I＝｛０，１，２，３，４｝，集合Ａ＝｛０，１，２，３｝，集合Ｂ＝｛２，３，４｝，则（C IA）∩（CI B）=__________.
★14、已知不等式5-x>7x+1与不等式ax2+bx-2>0的解集相同，则a=____；b=_____
★15、设非空集合A={x2a+1≤x≤3a-5}，B={x3≤x≤22}，则能使A
A∩B成立的a值的集合为__________。
▲●★选择题答案：
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
▲ ●★ 填空题答案：
11题：_______________; 12题: a=________________; 13题:________________
14题: a=________ b= _________; 15题:________________.
三、 解答题（12+12+12+12+13+14=75′）
★16、设U={x∈Z0<x≤10},A={1,2,4,5,9},B={4,6,7,8,10},C={3,5,7},求：
①、A∩B； ②、A∪B； ③、(CUA)∩(CUB)； ④、(CUA)∪(CUB)； ⑤、(A∩B)∩C； ⑥、(A∪B)∩C
★17、已知R为全集，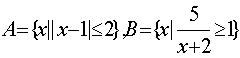
, 求 
。
★18、不等式
对于
恒成立，求
的取值范围
★19、已知集合A=｛xx2-5x+4≤0｝ B=｛xx2-2ax+a+2≤0｝若A∪B=A求a的取值范围
★20、已知M={x -2≤x≤5}, N={x a+1≤x≤2a-1}；（Ⅰ）若MN，求实数a的取值范围；（Ⅱ）若M
N，求实数a的取值范围.
★21题：如图,在某水渠同侧有甲、乙两个化工厂，为了保护环境，需将甲、乙两个工厂的污水经过处理之后再排入水渠，为此现设计有两种方案：
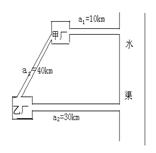方案一：在甲、乙两厂各建一个污水处理厂，分别处理本厂的污水，然后各自通过新建的管道a1（长10km）、a2(长30km)将污水处理之后再排入水渠；
方案二：只在甲厂修建一个污水处理厂，乙厂的污水则通过修复甲、乙两厂间的旧管道a3(长40km），然后经此输入污水处理厂，再将两厂的污水经过处理之后，通过新管道a1排入水渠。
已知建立污水处理厂的费用为M=60Q2（万元），辅设新管道的费用为N=6Q·L（万元），其中Q表示污水量（吨/秒），L表示管道长（km)，而又已知修复1km旧管道的费用仅是辅设1km新管道费用的25%；
（Ⅰ）、当乙工厂的污水排放量为5吨/秒时，记方案一中的总费用为W万元，记方案二中的总费用为P万元，设甲厂的污水排放量为Q1吨/秒，请写出W与Q1之间的函数关系式，以及P与Q1之间的函数关系式；
（Ⅱ）、在总费用不超过4200万元，且乙厂的污水排放量又为5吨/秒的条件下，若甲厂的污水排放量达到了3吨/秒以上，问应选择使用哪种方案，说明理由。
姓名_______ 湖南省省级示范性高中……洞口三中数学测验试卷(解答卷)
学号________ 高一《集合》单元测试试题（1）
班级_________ 撰稿： 方锦昌 电子邮箱 fangjingchang2 手机号码
一、选择题：
★1．设全集U＝R，集合A＝(1，＋∞)，集合B＝(－∞，2)。则U(A∩B)＝（
C ）
A．(－∞，1)∪(2，＋∞) B．(－∞，1)∪[2，＋∞)
C．(－∞，1]∪[2，＋∞) D．(－∞，1]∪(2，＋∞)
★2、已知A={1，a}，则下列不正确的是（ ）
Ａ：a∈A Ｂ：１∈Ａ Ｃ：（１，a）∈Ａ Ｄ：1≠a
★3、集合，，
之间的关系是（ C ）
（A） （B） （C） (D)
★4、如图，阴影部分所表示的集合为（ B ）
A 、A∩（B∩C） B、（CSA）∩（B∩C）
C、（CSA）∪（B∩C） D、（CSA）∪（B∪C）
★5、设I为全集，S1、S2、S3是I 上的三个非空子集，且S1∪S2∪S3=I，则下列 论断正确的是（ C ）
A、 CIS1∩（S2∪S3）=Æ B、 S1Í（CIS2∩CIS3）
C、 CIS1∩CIS2∩CIS3=Æ D、 S1Í（CIS2∪CIS3）
★6、设关于x的式子当x∈R时恒有意义，则实数a的取值范围是（ A ）
A、a≥0 B、a<0 C、a< D、 a≥0或a<
★7、设集合S=｛a,b,c,d,e｝,则包含｛a,b｝的S的子集共有（D ）个
A 2 B 3 C 5 D 8
★8、设集合M=｛xx= +,k∈Z｝,N=｛xx= +,k∈Z｝,则（ B）
A、 M=N B、 MÜN C、 MÝN D、 M∩N=Æ
★9、设⊕是R上的一个运算,A是R上的非空子集,若对任意的a、b∈A，有a⊕b∈A，则称A对运算⊕封闭，下列数集对加法、减法、乘法和除法（除数不等于0）四则运算都封闭的是（ C ）
A 自然数集 B 整数集 C 有理数集 D 无理数集
★10、设P、Q为两个非空实数集合，定义集合P+Q=，则P+Q中元素的个数是（ B ）
A．9 B．8 C．7 D．6
二、 填空题
★11、已知集合，，若，则实数的取值范围是
.
★12、Ａ＝｛a²,a+1,－3｝，Ｂ＝｛a－3,2a－1,a²+1｝，若Ａ∩Ｂ＝｛－３｝，那么a＝_______.
★13、设全集I＝｛０，１，２，３，４｝，集合Ａ＝｛０，１，２，３｝，集合Ｂ＝｛２，３，４｝，则（C IA）∩（CI B）=__________.
★14、已知不等式5-x>7x+1与不等式ax2+bx-2>0的解集相同，则a=__-4__；b=___-9__
★15、设非空集合A={x2a+1≤x≤3a-5}，B={x3≤x≤22}，则能使AA∩B成立的a值的集合为__________。
三、 解答题
★16、设U={x∈Z0<x≤10},A={1,2,4,5,9},B={4,6,7,8,10},C={3,5,7},求
A∩B,A∪B,(CUA)∩(CUB),(CUA)∪(CUB),(A∩B)∩C,(A∪B)∩C。
★17、已知R为全集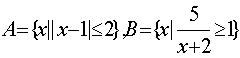，, 求 。
★18、不等式 对于 恒成立，求的取值范围
★19、已知M={x
-2≤x≤5},
N={x a+1≤x≤2a-1}；（Ⅰ）若MN，求实数a的取值范围；（Ⅱ）若MN，求实数a的取值范围.
解：（Ⅰ）由于MN，则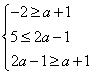
，解得a∈Φ.（Ⅱ）①当N=Φ时，即a＋1＞2a－1，有a＜2；
②当N≠Φ，则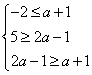
，解得2≤a≤3，综合①②得a的取值范围为a≤3.
★20、已知集合A=｛xx2-5x+4≤0｝ B=｛xx2-2ax+a+2≤0｝若A∪B=A求a的取值范围
解、A=｛x1≤x≤4｝若A∪B=A则BÍA；①、当B =Æ时,由△<0则-1<a<2；②、当B≠Æ时,由
△≥0
¦（1）≥0
¦（4）≥0
对称轴 1≤≤4 Þ2≤a≤ ∴｛a-1<a≤｝为所求
★21题：如图,在某水渠同侧有甲、乙两个化工厂，为了保护环境，需将甲、乙两个工厂的污水经过处理之后再排入水渠，为此现设计有两种方案：
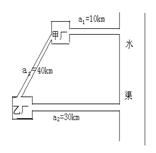方案一：在甲、乙两厂各建一个污水处理厂，分别处理本厂的污水，然后各自通过新建的管道a1（长10km）、a2(长30km)将污水处理之后再排入水渠；
方案二：只在甲厂修建一个污水处理厂，乙厂的污水则通过修复甲、乙两厂间的旧管道a3(长40km），然后经此输入污水处理厂，再将两厂的污水经过处理之后，通过新管道a1排入水渠。
已知建立污水处理厂的费用为M=60Q2（万元），辅设新管道的费用为N=6Q·L（万元），其中Q表示污水量（吨/秒），L表示管道长（km)，而又已知修复1km旧管道的费用仅是辅设1km新管道费用的25%；
（Ⅰ）、当乙工厂的污水排放量为5吨/秒时，记方案一中的总费用为W万元，记方案二中的总费用为P万元，设甲厂的污水排放量为Q1吨/秒，请写出W与Q1之间的函数关系式，以及P与Q1之间的函数关系式；（Ⅱ）、在总费用不超过4200万元，且乙厂的污水排放量又为5吨/秒的条件下，若甲厂的污水排放量达到了3吨/秒以上，问应选择使用哪种方案，说明理由。
解：①、W=60Q12+6Q1×10+60×52+6×5×30=60Q12+60Q1+2400
②、P=60（Q1+5）+25%×6×5×40+6（Q1+5）×10=60Q12+660Q1+2100
考察方案一：60Q12+60Q1+2400≤4200，则0≤Q1≤5，
考察方案二：60Q12+660Q1+2100≤4200，则0≤Q1≤<3
∴应使用方案一更好一些。
备选例题：
【★题22】已知集合A=｛ xx2-5x+4≤0｝B=｛xx2-2ax+a≤0｝，若A∪B=A，求a的取值范围
（解、｛a-1≤a≤｝）
【★题4】已知函数¦（x）=定义域为集合A，函数g（x）=lg[(x-a-1)(2a-x)]定义域为集合B,若BÍA求实数a的取值范围
解、集合A=｛xx<-1或 x≥1｝
①、当a<1时,B=(2a,a+1),则2a≥1或a+1≤-1； ∴｛a≤a<1或a≤-2｝
②、当a=1时,B=Æ 满足要求；③、当a>1时, B=(a+1,2a),则2a≤-1或a+1≥1则a>1
∴a∈[,+∞)∪(-∞,-2]为所求
★【题】、已知洞口县半江水库的最大库容量为128000m3，当山洪暴发时，估计注入水库的水量S（单位：m3)与天数n (n∈N*,N≤10）存在有下列函数关系式：S=5000；现在此水库的存水量已有80000 m3，在山洪暴发到来之时，水库方面将立即开闸放水泄洪，且每天的泄洪量是4000 m3，据此请你进行预测评估，在这10天当中水库的堤坝是否存在危险？若存在危险，说明是第几天或哪几天会发生危险；若不存在危险，请报告理由。
★【题】为保护我国某种特种水泥工业的发展，决定对进口的该种水泥征收附加税。已知此种日本产的水泥在我国的市场零售价为250元/吨时，每年的销售量为40万吨；现在当我国政府对其征收的附加税标准达到t吨/百元时，则每年该种水泥的销售量将减少t万吨，如果我国政府计划在该项经营中，使每年所征收的附加税收入不低于600万元，问该项附加税的税率应控制在哪个范围之内？
21.（本小题满分12分）
A、B两城相距100km，在两地之间距A城xkm处D地建一核电站给A、B两城供电，为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比，比例系数
.若A城供电量为20亿度/月，B城为10亿度/月.
（Ⅰ）把月供电总费用y表示成x的函数，并求定义域；
（Ⅱ）核电站建在距A城多远，才能使供电费用最小.
解：（Ⅰ）y=5x2+
(100—x)2（10≤x≤90）；
（Ⅱ）由y=5x2+(100—x)2＝
x2－500x+25000＝
＋
.
则当x＝
米时，y最小.
故当核电站建在距A城米时，才能使供电费用最小.