高一理科数学下期期中考试
高一理科数学试卷
命题教师:董九星 审题老师:赵志强
(考试时间：120分钟 试卷满分：150分)
考生注意：1.本卷分试卷部分和答题卷部分，考试结束只交答题卷；
2.所有答案必须写在答题卷指定位置上，写在其他地方一律无效。
第I卷（选择题，共60分）
一、选择题：（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）．
1．与
角终边相同的角的集合是
A．
B．
C．
D．
2.设
,
,
,则
的大小是
A、
B、
C、
D、
3.已知向量
，若
的大小为
A. 
B.
C.
D. 
4． 已知角
的余弦线是单位长度的有向线段;那么角的终边
A．在
轴上 B．在直线
上
C．在
轴上 D．在直线或
上
5.化简
得到的结果是
A、
B、
C、
D、
6．若向量
=（1，1），
=（1，－1），
=（－1，－2），则=
A． 
B．
C．
D．
7.若f(cosx)=cos2x-3cosx,则f(siny)的值域为
8．
9．已知函数
是以
为周期的偶函数，且
，那么
的值是
A
B
C
D
10.设
，
，
，当=λ+μ(λ，μ∈R)，且
时，点
在
A．线段AB上 B．直线AB上
C．直线AB上，但除去A点 D．直线AB上，但除去B点
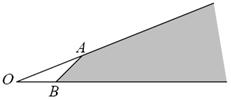
11．如右图所示，两射线
与
交于
，则下列选项中哪些向量的终点落在阴暗区
域(含边界)内
①
②
③
④
⑤
A．①② B．①②④ C．①②③④ D．③⑤
12．函数
是奇函数，则q等于
A、kp (kÎZ) B、kp+
(kÎZ) C、kp+
(kÎZ) D、kp－(kÎZ)
第Ⅱ卷（非选择题，共90分）
二、填空题：（本大题共4小题，每小题5分，共20分把答案填在题中横线上）．
13.
14．与向量
反向的单位向量是 。
15．已知
是⊙O上两点，
，则劣弧
长是 。
16．设集合
, 
. 给出
到 
的映射
. 关于点
的象
有下列命题： ①
；
②其图象可由
向左平移
个单位得到；
③点
是其图象的一个对称中心
④其最小正周期是
⑤在
上为减函数
其中正确的有
三、解答题：（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤）．
17.（本小题满分10分）
化简：
18.（本小题满分12分）已知
，
求
的值
19. （本小题满分12分）已知向量
，
，且
=
，求
．
20. （本小题满分12分）设函数
图像的
一条对称轴是直线
。
（Ⅰ）求
；
（Ⅱ）求函数
的单调增区间；
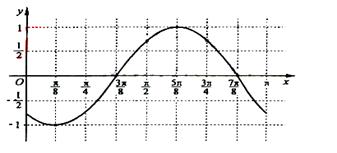
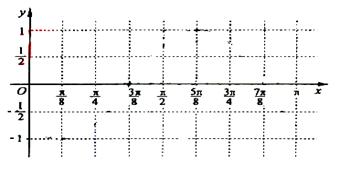
（Ⅲ）用描点法画出函数在区间
上的图像。
21．（本小题满分12分）已知
,
（1）把表示成cosx 的函数并求的定义域
（2）当
时，方程 f(x) =
(k∈R)有解，求k的取值范围。
22. （本小题满分12分）已知定义在
上的奇函数满足
，且在
上是增函数. 又函数
（1）证明：在
上也是增函数；
（2）若
，分别求出函数
的最大值和最小值；
（3）若记集合
，
，求
.
| 题号 | 一 | 二 | 三 | 总分 | |||||
| １７ | １８ | １９ | ２０ | ２１ | ２２ | ||||
| 分数 |
|
|
|
|
|
|
|
|
|
模拟答卷
一．选择题（共６０分）
| 题号 | １ | ２ | ３ | ４ | ５ | ６ | ７ | ８ | ９ | 1０ | 1１ | 1２ |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
 | |||
 | |||
|
|
|
|
高一理科数学参考答案
一.CADAA DAAAB AD
二.13. 
14. 
15. 
16. ①④⑤
三.17. 解:原式=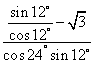
=
………………4分
=
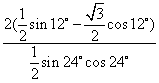……………………………10分
=
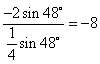………………………………12分
18.解：
……………………4分
又
=
+1 ………………………10分
=
………………………12分
19.解：
，
=
．
………………………………6分
由已知=，得
．
又
，所以
．
，
．
，
．
………………… 12分
20.解：（Ⅰ）
的图像的对称轴，
……………2分
……………4分
（Ⅱ）由（Ⅰ）知
………………………5分
由题意得 
……………6分
∴ 
…………………………7分
所以函数
…8分
（Ⅲ）由
| x | 0 |
|
|
|
|
| ||
| y |
| －1 | 0 | 1 |
|
|
|
…………………12分
21、解:①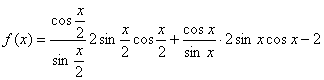
=
=2
……………………4分
由
得
∴定义域是｛x｜｝ ………………………6分
② ∵
且 ∴
……………8分
由2=
有解
即
有解 ∵
∴
，所以的取值范围是
………………………………12分
22.（1）证明：任取
，则
且在上是增函数，
.又为奇函数，
故
即
，在上也是增函数. ………………… 3分
（2）由
，
令
，则
，记
，由知，
函数
在
上是减函数，
故
时，有最大值
；
时，有最小值
. ……………7分
（3）由在，上是增函数，
或
，又，
所以
，
即
对
恒成立.
，
当
时取得. 
即
， 故
.
……………………………12分