高一第一学期期末中学教学质量调研监测

高一第一学期期末中学教学质量调研监测

高一数学试卷

（答题时间120分钟，满分150分）

范围：数学必修①和数学必修④一、三章

注意：本次考试允许使用科学计算器，但不得相互转借

一．选择题（本大题共12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项是符合题目要求的，请将正确答案的代号填在答卷的相应表格内）

1．已知：集合A={x｜0≤x≤，x∈Z}　B={x｜x=2a a∈A}　则：A∩B= _{-----------------------}

A .{0，2}　　　B.{0，1}　　 C.{1，2}　　　D.{0}

2．设集合P={3，4，5}，Q={4，5，6，7}，定义P·Q={(a,b) ｜a∈P,b∈Q},则P·Q中元素的个数为:_{-----------------------}

A. 3　　　　B. 7　　　　　 C.10　　　　　 D.12

3. 与函数y=10^lg(x-1)图象相同的函数是: _{----------------------------}

A.  y=x-1　　　　B. y=｜x-1｜　　　 C.　y=　　　 D. y=()²

4. 若0＜a＜1,x＞y＞1,下列关系式中不成立的个数是: _{---------------------------------}

① a^x＞a^y  ②x^a＞y^a  ③loga^x＞loga^y④logx^a＞logy^a

A . 4　　　　　 B. 3　　 　　C.　2　　　D. 1

5. 方程2^x-1+x=5的解所在区间是：_{------------------------------}

A. (0,1)　　　　　　  B. (1,2)　　　　　  C. (2,3)　　　　　　  D. (3,4)

6. 假设世界人口自1980年起，50内的增长率均固定，已知1987年世界人口达50亿，1999年第60亿个人诞生在赛拉佛耶，根据这些资料推测2023年世界人口数最接近下列哪一个数：_{---------------------------}-

A．92亿　　　　　　 B.86亿　　　　　  C.　80亿　　　　　  D. 75亿

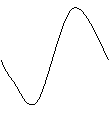
7. 函数y=Asin(ωx+φ),( ω＞0, ｜φ｜＜,x∈R)的部分图像如图所示,则函数表达式为: _{----------------------------------}

y

　　　　　　　　　　  A. y= -4sin(x+)　　 B.y=4sin(x-)

4

　　　　　　　　　　　  C. y= -4sin(x-)　　D. y=4sin(x+)

8. 已知函数y=2sinωx (ω＞0)的图象与直线y+2=0的相邻两个公共点之间的距离为，则ω的值为：_{-----------------------}

A. 3　　　　　　  B. 　　　　　　C. 　　　　　　　D.

9. 已知cosө=, ө∈(0,π) ,则cos(π+2 ө)= _{--------------------------}

A.  -　　　 B.　-　　　　 C. 　　　　D.

10. 在sinx+cosx=2a-3中，a的取值范围是：_{-----------------------------}

A. ≤a≤　　　　　　　　　　　　　　 B.a≤

C.  a＞　　　　　　　　　　　　　　　　 D. -≤a≤-

11．已知函数 f(x)=lg,若f(a)=b,则 f(-a)=_{----------------------------}

A.b　　　B . -b　　　　　  C.　　　　　 D. _

12.已知定义在区间[0，1]上的函数y=f(x),图象如图所示，对满足0<x₁〈x₂<1的任意x_1,,

x₂给出下列结论：

①　　

y

f(x₁)-f(x₂)>x₂-x₁;

②　　

1

xf(x)>xf(x);

③　　 　<f().

x

o

1

其中正确的结论有

A.0个　　　B.1个　　　　　 C.2 个　　　　　　  D.3个

二，填空题（本大题共6小题，每小题5分，共30分，请将正确答案填空在答卷上）

13. 定义f (x, y)=(y², 2y-x)，若f (m, n)=(1,2)，则 (m,n)= _{----------------------------------------------。}

14．已知f (x) 是奇函数，且当x＞0时，f(x)=x (1+x), 那么当x＜0时f(x)的解析式为：

_{---------------------------}

｜x｜-1, x≤1 2-2x,　 x＞1

15．已知函数f(x)={｛｝　　　　　　　　　　  若f (a)=1, 则a= _{-----------------------------------------}

16. 如果函数f (x) = x²+ mx + m +3的一个零点在原点，则另一个零点是：_{--------------------------------------}

17. 设函数f (x)=sin(ωx+φ),( ω＞0， ｜φ｜＜)给出以下的四个论断：

① 它的最小正周期为π　　　 ② 它的图象关于直线x=成轴对称图形

③ 它的图象关于点（，0）成中心对称图形

④在区间〔-，0〕上是增函数，以其中的两个论断作为条件，另两个作为结论，写出你认为正确的一个命题：_{---------------------}

18．已知∈（，π）且sin=,则sin²+=  _{-------------------------------}

三．解答题（本大题共5小题，每题12分，共60分，请将详细解答过程写在答卷上）

19.已知函数f(x)=sin(2x+)+,x∈R

(1) 求函数f(x)的最小正周期和单调增区间;

(2) 函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样变换得到?

20．已知全集I=｛1、3，x³+3x²+2x｝;A=｛1, ｜2X-1｜｝如果C_IA=｛0｝,则这样的实数x是否存在?若存在,求出x;若不存在,说明理由.

21.已知函数f(x)=(1-tanx)[1+sin(2x+)] ,求:

(1) 函数f(x)的定义域,值域.

(2) 写出f(x)的单调递增区间.

22.函数f (x)= (a,b是非零实常数)，满足f(2)=1且方程f(x)=x,有且仅有一个解

(1)求a,b的值

(2)是否存在实常数m,使得对定义域中任意的x,有f(x)+f(m-x)=4恒成立?为什么?

23．设定义在R上的函数f (x)，满足当x＞0时，f(x) ＞1且对任意的x,y ∈R都有f(x+y)=f(x) ·f(y),f(1)=2

（1）求f(0)

(2) 求证：对任意的x∈R,都有f(x)>0;

(3) 解不等式：f(3x-x²) ＞4

(4) 解方程 [f(x)]²+f(x+3)=f(2)+1

珠海市2007-2008学年度第一学期期末中学教学质量调研监测

　　　　 高一数学试卷参考答案及评分标准

一．选择题（本大题共12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项是符合题目要求的，请将正确答案的代号填在答卷的相应表格内）

题目	1	2	3	4	5	6	7	8	9	10	11	12
答案	A	D	D	C	C	B	A	A	C	A	B	C

二．填空题（本大题共6小题，每小题5分，共30分，请将正确答案填空在答卷上）

13．（0，1）或（-4，-1）　　　　14。x(1-x)　　　　　　 15.-2

16.3　　　　  17.①②③④或①③②④　　　　　 18。-

三．解答题（本大题共5小题，每题12分，共60分，请将详细解答过程写在答卷上）

19．（1）f(x)的最小正周期T==.由题意得2k-2x+2k+,kZ,即k-x k+, kZ, f(x)的单调增区间为[k-， k+], kZ--------------5分

　 （2）先把y=sin2x图象上所有点向左平移个单位长度，得到y=sin(2x+)的图象，再把所得图象上所有的点向上平移个单位长度，就得到sin(2x+)+的图象----------10分

20.因为C_IA=｛0｝,所以0I，0A, 所以x³+3x²+2x=0，---------2分　　 即x(x+1)(x+2)=0，所以x₁=0,x₂=-1 x₃=-2.----------4分　　　当x=0时，｜2X-1｜=1,这与集合元素的互异性矛盾，舍去；---------------6分　　 当x=-1时，｜2X-1｜=3符合题意；----------8分　　  当x=-2时，｜2X-1｜=5,但此时5I，舍去。----------9分　　　 综上所述，存在唯一实数x=-1，使得C_IA=｛0｝.--------------10分

21. f(x)=(1-)(1+sin2xcos+cos2xsin)

　　　 =(1-)(2sinxcosx+2cos²x)

　　　 =2(cosx-sinx) (cosx+sinx)

　　　 =2( cos²x- sin²x)

　　　 =2cos2x---------------------------4分

(1)　f(x)的定义域{xx R,x≠k+, kZ },2x≠2k+,kZ,2cos2x≠-2,函数f(x)的植域为（-2，2]--------------------------7分

(2)　  令2k-<2x2k,(kZ)得k-<xk （kZ），函数f(x)的单调递增区间是（k-，k](kZ)。---------------------------10分

22．（1）由 f(2)=1得2a+b=2.又x=0显然是方程=0的解,变形得x[ax+(b-1)]=0 ax+(b-1)=0无解或有解为0。若无解，得a=0,与已知矛盾；若有解为0，则b=1,所以a=,

故b=1,a=。----------------------4分

（2）由（1）知f(x)= ,设存在实常数m,使得对定义域中任意的x,有f(x)+f(m-x)=4恒成立，取x=0,则f(0)+f(m-0)=4,即=4,m=-4,又m=-4时，f(x)+f(-4-x)= +=4成立，所以存在实常数m=-4, 使得对定义域中任意的x，有f(x)+f(m-x)=4恒成立。------------------------10分

23．（1）f(x)=f(x+0)=f(x)f(0).故f(0) ≠0. x>0时,f(x)>1,又f(0)= [f(0)]²f(0)=1.-----------------------2分

(2)f(x)=f(+)=[f()]²≥0.假设存在某个x₀R,使f(x₀)=0,则对任意x>0，有f(x)=f[(x-x₀)+x₀]= f(x-x₀)f(x₀)=0,与已知矛盾，xR均满足f(x)>0--------------------4分

(3)任取x_1, x₂R且x_1< x_2,  则x₂-x₁>0,故f(x₂-x₁)>1.  f(x₂)-f(x₁)= f[(x₂-x₁)+x₁]-f(x_1, )= f(x₂-x₁) f(x₁)- f(x₁)= f(x₁) f[(x₂-x₁)-1]>0,  xR时, f(x)为单调递增函数。 f(1)=2，则f(2)= f(1) f(1)=4。f(3x-x²)>4= f(2), 3x-x²>2,即1〈x<2. 不等式的解集为{x1〈x<2.}.--------------------------------7分

(4) f(3)= f(1+2)= f(1) f(2)=8, 方程 [f(x)]²+f(x+3)=f(2)+1可化为[f(x)]²+f(3) f(x)=5,即[f(x)]²+4f(x)-5=0,解得f(x)=1或f(x)=-5（舍），由（1）得x=0故原方程的解为x=0.-------------------------------------------10分

命题人：红旗中学　　吴文双

　　　　　　　 2008-1-8