高一（下）第二次阶段考数学试卷
命题：黄远忠 审核：洪幼文
悄悄提醒：注意掌握时间，会做的要先做，不要放弃任何得分的机会！
一、选择题（每小题5分，共60分）
1．在
间，与角
终边相同的角是（ ）
A、
B、
C、
D、
2．若
是第一象限角，下列各角中是第四象限角的是（ ）
A、
B、
C、
D、
3．函数
的最小正周期是（ ）
A、
B、
C、
D、
4．若
，则P为（ ）
A、
B、
C、
D、
5．化简
的结果是 ( )
A、
B、
C、
D、
6．已知
，则
和
都是增函数的区间是（ ）
A、
B、
C、
D、
7．已知扇形的周长是6cm，面积是2 
，则扇形的圆心角的弧度数是（ ）
A、1 B、4 C、1或4 D、2或4
8．下列各组函数值的大小关系正确的是（ ）
A、
B、
C、
D、
9．函数
的图象（ ）
A、关于点
对称 B、关于直线
对称
C、关于点
对称 D、关于直线
对称
10．点P从（1，0）出发，沿单位圆
按顺时针方向运动
弧长到达Q点，则Q的坐标为（ ）
A、
B、
C、
D、
11．在
上既是增函数，又是奇函数的是（ ）
A、
B、
C、
D、
12．方程
的实数解的个数是（ ）
A、3 B、4 C、5 D、无穷多
二、填空题（本大题共4小题，每小题4分，共16分）
13．求值：
。
14．若
，则
= 。
15．函数
的单调递增区间为
。
16. 若函数
同时满足条件：①在区间
内为增函数；②
；③最小正周期为，则这样的解析式为________
__________.(注：填上你认为正确的一个解析式即可，不必考虑所有情况)
三、解答题（本大题共6小题，共74分，解答题应写出文字说明、证明过程或演算步骤）
17. （本题满分10分）求值：
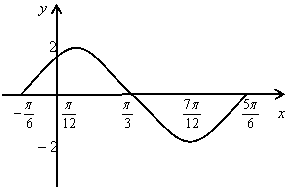
18．（本题满分12分）如图表示函数
的一段图象，试根据图象确定函数的解析式，并写出图象对称中心的坐标。
19．（本题满分12分）用“五点法”画出函数
，
在长度为一个周期的闭区间上的图象，并指出的振幅、初相、频率和对称轴。
20．（本题满分12分）已知函数
。
（1）求函数的最小正周期；
（2）若
，求函数的递减区间；
（3）该函数图象可由正弦曲线
经过怎样的变换得到的？
21．（本题满分14分）已知A为三角形ABC的内角，且满足
．
（1）求
的值； （2）
的值．
22.（本题满分14分）已知函数
.
（1）当
且
时，求函数的值域；
（2）当，试讨论函数的最大值。
高一（下）第二次阶段考数学试卷参考答案
一、1~4、DCBB 5~8、ADCD 9~12、ACAC
二、13. 
14. 
15.
（注：写成开区间也对）(
未写扣1分)
16. 如：
，
，
，……
三、17. 
18.解：由图知：
，
， ∴
∵
，
∴
， ∴
∵点
在图象上， ∴
。∴
，
∵
，∴
，∴所求的函数解析式为：
。
由上易得图象对称中心的坐标是
。
19.解：列表
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 | 2 | 0 | －2 | 0 |
|
| ||||||||||||||
|
| ||||||||||||||
描点、连线如图所示。
振幅，初相
，频率
，由
得
∴对称轴方程是
20.解：（1）
；
（2）由
及得：
函数的递减区间是
；
（3）
21.解：（1）由两边平方得：
∴
则
，即
∵A为三角形ABC的内角，且
，∴A为钝角。
∴
。
（2）由上易求得
，
，∴
∴原式＝……＝
。
22.解：（1）
，
令
，则
，
，∴
，∴函数的值域是
。
（2）由已知可得
，
令，则
∵，
∴
。
①当
即
时，
在
上单调递减，∴
；
②当
即
时，
；
③当
即
时，在上单调递增，∴
。