高一数学第一学期期中考试
数 学 试 题
考生须知: (试题录入: 陕西省渭南吝店中学 郝进)
1.本试题共4页, 考试时间为100分钟.试题由基本题(100分)和附加题(20)分组成.基本题为每个学生必答题, 附加题由学有余力的学生选用. 考试时间: 2007－11－09
2.在答题前,同学们务必在答题卡上填上你的学校、班级、姓名、学号.
3.答题时请同学们在答题卡上做答,考试结束时只交答题卡.
一、选择题(本大题共10个小题,每小题4分,共40分)
1. 若A={a,b,1},则
A.1∈A B. 1
A C. a=1 D. b=1
2.
已知函数
的定义域为M, 则M=
A. {xx>1} B.{xx<1} C. {x－1<x<1} D. Æ
3.
设集合U={1,2,3,4,5}, A={1,2,3},B={2,5}, 则A∩(
UB)=
A.{2} B.{2,3} C.{3} D.{1,3}
4.
函数y=
在[0,1]上的最大值为2, 则a=
A. 
B.2 C. 4
D. 
5. 对于a>0, a≠1, 下列结论正确的是
A. 若M=N , 则 
B. 若, 则M=N
C. 若
, 则M=N D.
若M=N, 则
6.
三个数: 
, 
, 
的大小是
A. >
> B. >>
C. >> D. >>
7.
已知函数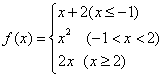
, 若f(a)=3 , 则a的值为
A. 
B. －
C. ±
D.以上均不对
8.
已知集合A={1,2,3}, B={2,4}, 定义集合A、B之间的运算, A*B={xx∈A且xB}, 则集合A*B等于
A.{1,2,3} B.{2,4} C.{1,3} D.{2}
9. 设A={x0≤x≤2},B={y1≤y≤2}, 在图中能表示从集合A到集合B的映射是
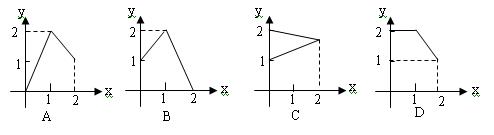
10.
已知
是奇函数, 则
＋
的值为
A. 2008 B.2007 C.2006 D.2005
二、填空题(本大题共3小题, 每小题4分,共12分)
11.
函数
的图象与函数
(x>0) 的图象关于直线y=x对称, 则f(x)=
12.
函数
在定义域[0,2]上的值域为: .
13.
已知函数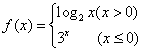
, 则
的值是
.
三、解答题(本大题4小题, 共48分.解答写出文字说明,证明过程或演算步骤)
14. (本小题满分12分)
化简求值
(1) 
＋
＋
＋
－
(2) lg14－
＋lg7－lg18
15. (本小题满分12分)
判断
在x∈[0,＋∞)的单调性, 并用定义证明.
16. (本小题满分12分)
已知函数
(1)求f(x)的定义域;
(2)当x= 时, 求
的值;
(3)判断函数的奇偶性.
17. (本小题满分12分)
某商品在近30天内每件的销售价格P元与时间t天的函数关系式是
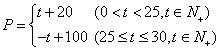
该商品的日销售量Q件与时间t天的函数关系式是Q=－t＋40 (0<t≤30, t∈N＋)
(1)求这种商品的日销售金额y关于时间t的函数关系式;
(2)求这种商品的日销售金额y的最大值,并指出取得该最大值的一天是30天中的第几天?
四、附加题 (本大题共3小题, 共20分)
18. (本小题满分5分)如图,液体从一圆锥漏斗漏入一圆柱桶中,开始漏斗盛满液体,经过3分钟漏完,若圆柱中液面上升速度是一常量, H是圆锥漏斗中液面下落的距离. 则H与下落时间t分钟的函数关系表示的图象可能是( )
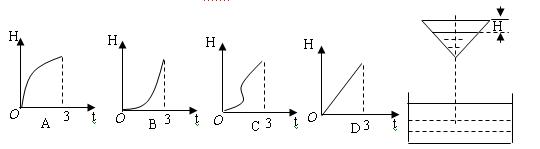
19.
(本小题满分5分)若一次函数
(a≠0)有一个零点2, 那么函数
的零点是
20. (本小题满分10分)
已知a是实数, 函数
. 求函数在区间[0,1]上的最小值.
高一期中考试
数学试题参考答案及评分标准
一、选择题(本大题共10个小题,每小题4分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | D | B | B | D | A | C | D | A |
二、填空题(本大题共3小题, 每小题4分,共12分)
11. 
12. 
13. 
三、解答题(本大题4小题, 共48分.解答写出文字说明,证明过程或演算步骤)
14.(12分)
解:
(1)原式= 
(6分)
(2)原式= 
(6分)
15. (12分)
证明: 任取0≤x1<x2,
则f(x2)－f(x1)=1－2x
－1＋2
= 
= 2(x1－x2)(x1＋x2)
(6分)
∵ 0≤x1<x2, ∴x1－x2<0, x1＋x2>0
∴f(x2)－f(x1)<0, 即f(x2)<f(x1)
故f(x)=1－2x2在[0,＋∞)上为单调减函数 (12分)
16.(12分)
解: (1)函数的定义域为(－1,1) (4分)
(2)当x= 时, 
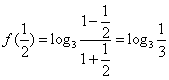= －1
(8分)
(3) ∵ f(－x)= 
= 
=－
=－f(x)
∴ 函数f(x)为奇函数 (12分)
17.(12分)
(1) 解析式为: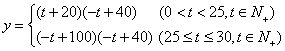 
(4分)
(2)当0<t<25, t∈N＋时, y=PQ=(t＋20)(－t＋40)=－t2＋20t＋800=－(t－10)2＋900
∴ t=10(天)时, ymax=900(元) (8分)
当25≤t≤30, t∈N＋时, y=PQ=(－t＋100)(－t＋40)=t2－140t＋4000=(t－70)2－900
而y=(t－70)2－900在t∈[25,30]时,函数递减.
∴t=25(天)时, ymax=1125(元) ∵1125>900, ∴ymax=1125(元)
故所求日销售金额的最大值为1125元,且在最近30天中的第25天日销售额最大 (12分)
四.选作题 (本大题共3小题, 共20分)
18. (5分) B
19. (5分) 0, －
20. (10分)
解: 由a≠0可知, 二次函数
=
= 
(3分)
所以(1)当－ <0, 即a>0时, 函数y=f(x)在区间[0,1]上是单调递增函数,
所以函数的最小值是f(0)=－a－3 (5分)
(2)当 － >1 ,即－1<a<0时, 函数y=f(x)在区间[0,1]上是单调递减函数,
所以函数的最小值是f(1)= －1 (8分)
(3)当0<－ ≤1, 即a≤－1时, 函数y=f(x)在区间[0,1]上的最小值是
f()=－a－3 (10分)