高一数学第一学期期中考试试题（普通班）
祝同学们考试愉快，快乐考试！
考生注意：
1. 本试卷共分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，考试时间为120分钟，满分150分。
2. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、试题科目用铅笔涂写在答题卡上。
3. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。
4. 答第Ⅱ卷前，请将密封线内的内容填写上。
5. 本试卷主要考试内容：第一章 集合与简易逻辑，第二章 函数（2.1～2.6）（包括函数的奇偶性的内容）。
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有且只有一项符合题目要求.
1.函数
的定义域为
，则函数
的定义域为（ ）
A.
B.
C. D.
2. 设
，集合
，则
（ ）
A．1
B．
C．2
D．
3.集合
到集合
的映射
中满足
的映射个数是（ ）
A.1个 B.2个 C.3个 D.4个
4.设集合
，则
（ ）
A.R B.
C.{0}
D. 
5．函数
的图象关于（ ）对称
A.x轴 B.原点 C. y轴 D.直线y=x
6.一个面积为100cm2的等腰梯形，上底长为x cm，下底长为上底长的3倍，则把它的高y表示成x的函数为（ ）
A.
B. 
C.
D. 
7.设
，则（ ）
A.
B. 
C. 
D. 
8. 已知条件
：
，条件
：
，且
是
的充分不必要条件，则
的取值范围可以是（ ）
A.
B.
C.
D.
9. 函数
的图象大致是 ( )
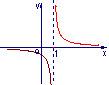
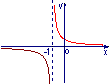
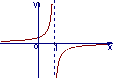
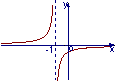
A B C D
10.已知函数
的图象与函数
的图象关于直线
对称，则
（ ）
A.2
B.0
C.1
D.
11.关于函数
的单调性，下列说法中正确的是（ ）
A.在
上是减函数
B.在
上是增函数
C.在
上是减函数
D.在
上是增函数
12. 已知函数
的反函数为
则函数
的值域是（ ）
A.
B.
C.
D.
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡相应的位置上.
13. 已知全集
，集合
，则满足条件的集合
共有_________个.
14.已知
，则
.
15. 已知函数
,则函数的值域为
.
16. 已知函数
存在反函数
，若函数
的图象经过点
，则函数的图象必经过点 ．
三、解答题：本大题共6小题，共70分。解答应写出必要的文字说明、证明过程及演算步骤.
17.（本小题满分10分）
已知
（1）若
，求实数的取值范围；
（2）若
，求实数的取值范围。
18.（本小题满分12分）
证明函数
是
上的增函数
19.（本小题满分12分）
已知为一次函数，且
，求的解析式。
20.（本小题满分12分）
已知
是定义在R上的奇函数
（1）求的值及的解析式；
（2）求的值域。
21.（本小题满分12分）
有甲、乙两种商品，经营销售这两种商品所能获得的利润依次为和（万元），它们与投入资金
（万元）的关系有经验公式
。
今有3万元资金投入经营甲、乙两种商品，为获得最大利润，对甲、乙两种商品的资金投入分别应为多少？能获得多大的利润？
22.（本小题满分12分）
已知函数
（1）求函数的定义域；
（2）若在区间
上有意义，求实数的取值范围。
高一数学参考答案及评分标准
说明：
1．本解答只给出了一种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．
2．对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．
3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．
4．只给整数分数，选择题和填空题不给中间分数．
一、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 | A | C | D | B | B | C | D | A | B | A | C | D |
二、填空题（每小题5分，共20分）
13. 8
14. 3 15. 
16. 
三、解答题
17.解：
…………………2分
…………………………………4分
（1）若，则有
，故
………………………7分
（2）若，则有
，故
………………………10分
18.证明：设
，且
……………………………2分
则
…………………6分
……………………………………………………8分
，即
………………………………10分
故是上的增函数………………………………12分
19.解：
依题意可设
……………………………2分
则
…………………4分
…6分
由已知有：
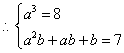………………………………………………………………8分
解得
……………………………………………………………………10分
故
……………………………………………………………………12分
20.解：
（1）
是奇函数且在
处有定义……………………………………2分
∴
…………………………………4分
从而
…………………………………………………………6分
（2）由
，得
……………………………………………8分
∵
的值域为
，
……………………10分
解得
故的值域为…………………………………………12分
21.解：设对乙商品投入资金
万元，则对甲商品投入
万元，
所获利润分别为
…………………………………4分
从而投资甲乙两商品所获得的总利润为
………………………6分
……………………………8分
当
即
时，
取得最大值
…………10分
故对甲乙两商品分别投入0.75万元和2.25万元时，总利润最大，最大利润为
1.05万元………………………………………………………………12分
22.解：
（1）当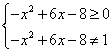
，……………………………………………2分
即
，且
时，函数有意义…………………………………4分
故的定义域为
…………………………………………6分
（2）由题设有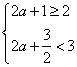（Ⅰ）
或（Ⅱ）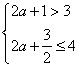
……………8分
由（Ⅰ）得
由（Ⅱ）得
……………………………………………………10分
故实数的取值范围是
…………………………………12分